A fast parallel algorithm for finding the longest

A fast parallel algorithm for finding the longest common sequence of multiple biosequences. Yixin Chen, Andrew Wan, Wei Liu Washington University / Yangzhou University December 2006

Biological Review § DNA can be represented as sequence of four letters (ACGT). § New biosequences every day. § Sequence comparison. § Find similarities with other sequences already known. § Longest Common Subsequence (LCS).

Longest Common Subsequence LCS § Search a substring that is common and longest to two or more given strings. § Searching for the LCS of multiple biosequences is a fundamental task in Bioinformatics. § LCS is a special case of global sequence alignment. § All algorithms of global sequence alignment can be used to solve LCS.

Longest Common Subsequence LCS Algorithms and complexity § Dynamic programming. § Smith-Waterman algorithm § Complexity O(mn). § Mayers and Miller § Complexity O(m+n). § Parallel algorithms. § CREW-PRAM

Longest Common Subsequence LCS Algorithms and complexity in Multiple sequences § What is the problem with those Algorithms? § Smith-Waterman: complexity now is exponential. § Carrillo and Lipman algorithm. § New divide and conquer algorithm DCA. (Stoye) § Clustal-W (Feng and Doolittle’s algorithm).

FAST_LCS § Seeks the successors of initial identical character pairs. Tables § Pruning operations § FAST_LCS can be extended to find LCS of multiple biosequences. § They it implemented using Parallel computing model as well.

Initial identical character pair and its successor table § Let X and Y be two biosequences, where Xi and Yi to { A, C , G, T } § Define an Array CH of four CHaracters: CH(1) = A CH(2) = C CH(3) = G CH(4) = T

Initial identical character pair and its successor table § Build the successor table of identical characters for two strings, Lets call the tables TX for sequence X an TY for sequence Y. The table(s) are defined as follows: TX(i, j) = min { k | k SX (i, j) } Otherwise SX(i, j) Where SX (i, j) = {k | Xk = CH(i), k > j } and i = 1, 2, 3, 4 and j = 0, 1, …n For example if i = 1 means A

Example Let X = “TGCATA” and Y = “ATCTGAT” If Xi = Yi = CH(k) then call them an identical pair CH(k) and denote as (i, j). Let (i, j) and (k, l) be two identical characters pairs of X Then: If i < k and j < l they call (i, j) a “predecessor” of (k, l). or (k, l) the a “successor” of (i, j)

Successor Table for example Remember the sequence X = “TGCATA” SX(1, 0) = k | Xk = CH(A) , k > 0 then k = {4 , 6} TX(1, 0) = min { 4, 6} => TX(1, 0) = 4. . . SX(1, 4) = k | Xk = CH(A) , k > 4 then k = {6} TX(1, 4) = 6

Example The final Tables are these: SX(1, 0) = 4 SX(1, 5) = 6 SX(1, 1) = 4 SX(1, 6) = - SX(1, 2) = 4 SX(1, 3) = 4 SX(1, 4) = 6 ” TGCATA

Some definitions § If Xi=Yi=CH(k) they call them “Identical pair of CH(k)” and it denoted as (i, j). § The set of all “Identical pairs” of X is denoted as S(X, Y). § If an identical pair (i, j) S(X, Y) and there is not (k, l) S(X, Y) such that (k, l) < (i, j) then they call (i, j) “initial identical pair”

Some definitions The level of each pairs is defined as follows:

Theorems T 1: If the length of LCS of X and Y is denote as |LCS(X, Y)| then |LCS(X, Y)| = max {level(i, j) | (i, j) S(X, Y)} T 2: For an identical character pair (i, j) S(X, Y) the operations of producing all its direct successors is as follows:

Back to the Example The successors of the pair (2, 5) are: (4, 6), (3, -), (-, -), (5, 7)

Example The successors of the pair (2, 5) are: (4, 6), (5, 7)

Pruning operations Operation 1 § If on the same level, there are two identical character pairs (i, j) and (k, l) > (i, j) then (k, l) can be pruned without to affecting the correctness of the algorithm § This operation will remove all the redundant identical pairs

Back to the Example The successors of the pair (2, 5) were (4, 6), (5, 7) since they are on the same level and (4, 6) > (5, 7) The successors of the pair (2, 5) is: (4, 6)

Pruning operations Operation 2 § If on the same level, there are two identical character pairs (i 1, j) and (i 2, j) and i 1< i 2 then (i 2, j) can be pruned without to affecting the correctness of the algorithm

Pruning operations Operation 3 § If on the same level, there are two identical character pairs (i 1, j), (i 2, j), …, (ir, j) and i 1< i 2 … < ir then : (i 2, j) … (ir, j) can be pruned

FAST_LCS complexity § They claim that the complexity of their algorithm is O(L) where L is the number of the identical character pairs of X, Y. § When they algorithm is implement using Parallel computing the complexity is O(|LCS(X, Y)|)

FAST_LCS and multiple sequences § FAST_LCS can be easily extended to the LCS problem of multiple sequences. § From the biological point of views is more important to find LCS for multiple sequence.

FAST_LCS and multiple sequences § Suppose there are n sequence X 1, X 2, …, Xn where X= (Xi 1, Xi 2, …, Xi, ni), ni is the length of Xi, Xij to { A, C , G, T } and where j = 1, 2, 3…, ni. § The successors tables will be denoted as: TX 1, TX 2, …. , TXn Where TXs is a two dimesional array for the sequence Xs=(Xs 1, Xs 2, … Xns), s = 1, 2, …, n

FAST_LCS and multiple sequences Following the same procedure that it is used to find two sequences, in this case start building the successors tables of all the sequences, following:

FAST_LCS and multiple sequences § Identical character tuple for LCS of multiple sequences. § The level of each tuple comes from the following:

FAST_LCS and multiple sequences § For an Identical character tuple this operation follows: § They claim two more Theorems which are basically the extension of T 1 and T 2 for multiple sequence

Example § Let n = 3, X 1 = “TGCATA”, X 2=“ATCTGAT” and X 3=“CTGATTC” § The successors tables are:

Example The direct successors of the identical character triple (1, 2, 2) can be obtained by :

Example § The successors are : (4, 6, 4), (3, 3, 7), (2, 5, 3), (1, 2, 2). § Then following the algorithm, apply the pruning operations we get (3, 3, 7), (2, 5, 3), (1, 2, 2), etc.

FAST_LCS for multiple sequence. complexity § The time complexity of most algorithms for multiple sequence LCS depends on the number of sequence. § They are not practicable when the number of sequence is large.

FAST_LCS for multiple sequence. complexity § When FAST_LCS algorithm is implement using Parallel computing the complexity is O(|LCS(X 1, X 2, … Xn)|). § It complexity is “Independent of the number of sequences n”

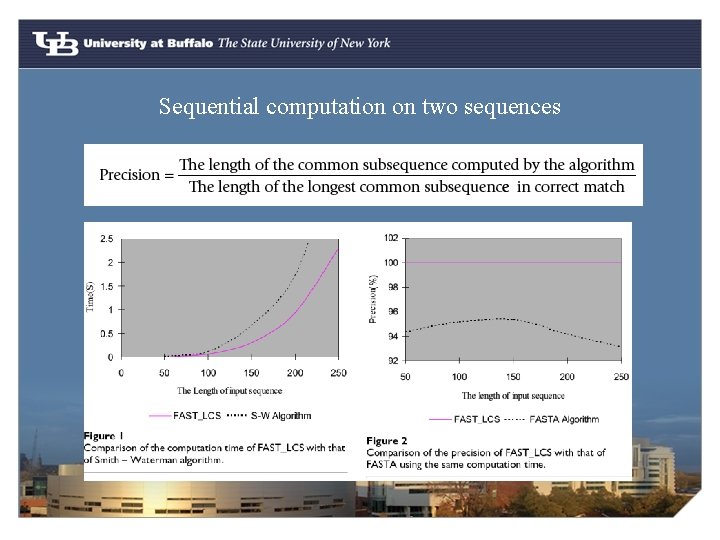
Sequential computation on two sequences

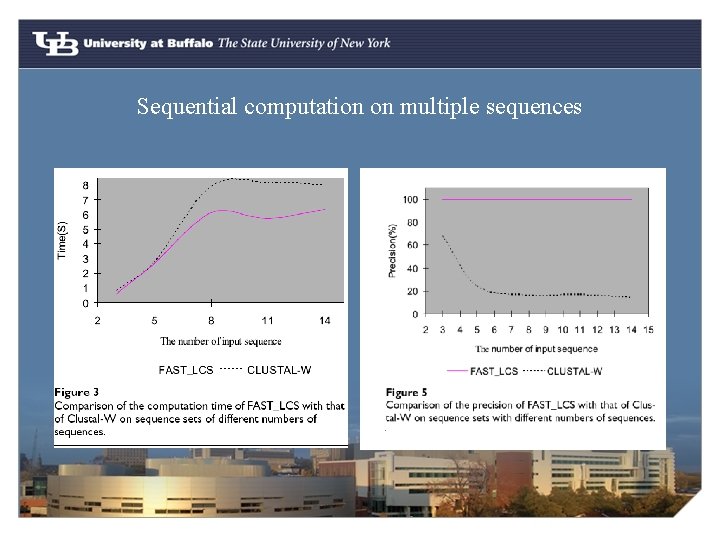
Sequential computation on multiple sequences

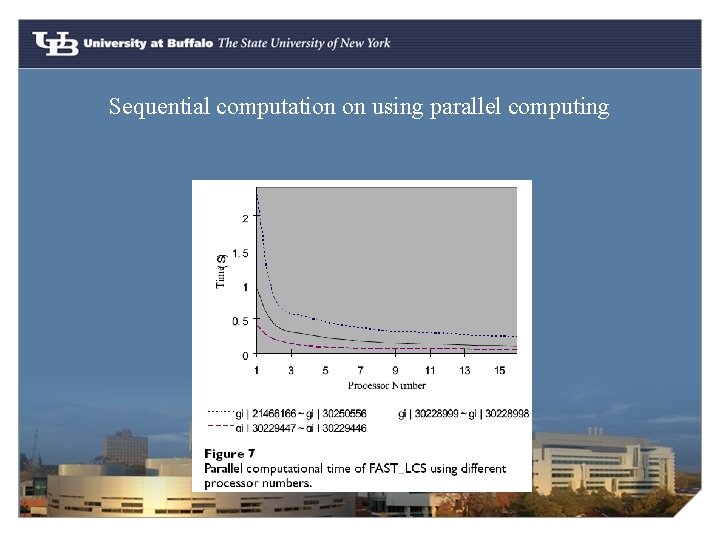
Sequential computation on using parallel computing

Conclusion § The precision of FAST_LCS is higher than FASTA and faster than S-W algo for computation on two sequences § FAST_LCS is faster than other algorithms that compute LCS for multiple sequences, like CLUSTAL-W. § FAST_LCS could be implemented using Parallel computation.