A Design Method for MIMO Radar Frequency Hopping

A Design Method for MIMO Radar Frequency Hopping Codes Chun-Yang Chen and P. P. Vaidyanathan California Institute of Technology Electrical Engineering/DSP Lab Asilomar Conference 2007

Outline § Review of the background – Ambiguity function in MIMO radar § The proposed waveform design method – – Ambiguity function for MIMO pulse radar Frequency hopping signals Optimization of the frequency hopping codes Examples § Conclusion and future work Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 2

1 Review: Ambiguity function in MIMO radar 3

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 4

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. (t, n) target u(t) TX t: delay n: Doppler Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 5

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. (t, n) target u(t) TX y(t, n) (t) RX t: delay n: Doppler Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 6

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. Matched filter output (t, n) target u(t) TX y(t, n) (t) RX t: delay n: Doppler Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 7

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. Matched filter output (t, n) target u(t) TX y(t, n) (t) RX t: delay n: Doppler Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 8

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. Matched filter output (t, n) target u(t) TX y(t, n) (t) RX t: delay n: Doppler Ambiguity function Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 9

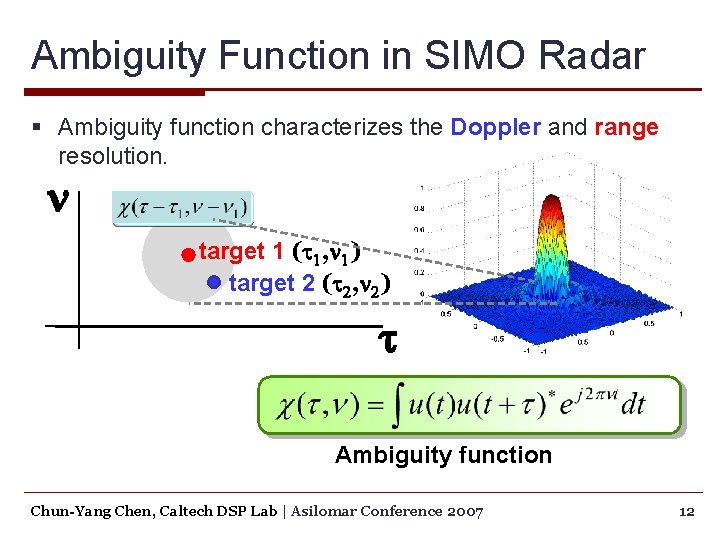
Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. n target 1 (t 1, n 1) target 2 (t 2, n 2) t Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 10

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. n target 1 (t 1, n 1) target 2 (t 2, n 2) t Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 11

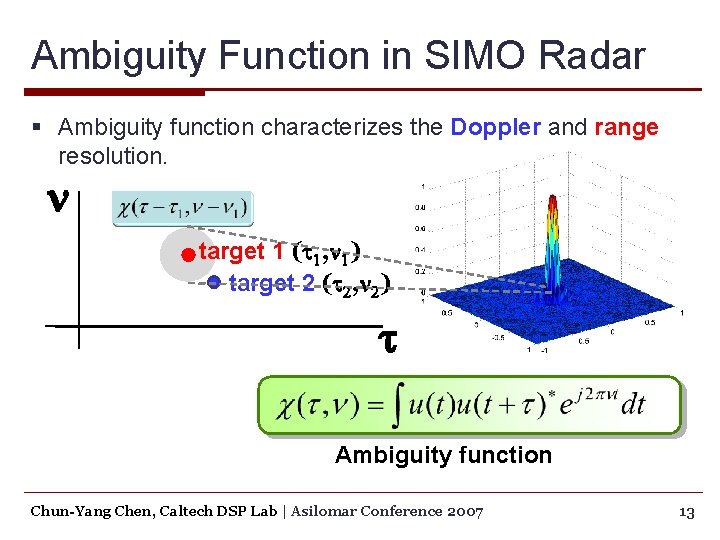
Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. n target 1 (t 1, n 1) target 2 (t 2, n 2) t Ambiguity function Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 12

Ambiguity Function in SIMO Radar § Ambiguity function characterizes the Doppler and range resolution. n target 1 (t 1, n 1) target 2 (t 2, n 2) t Ambiguity function Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 13

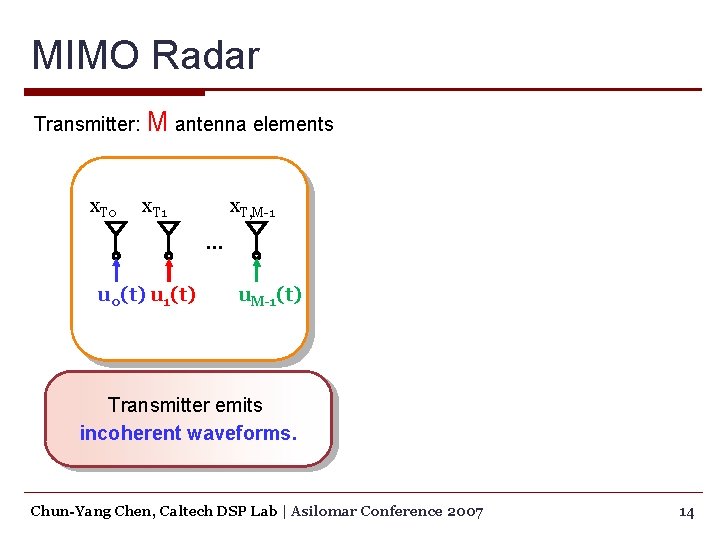
MIMO Radar Transmitter: M antenna elements x. T 0 x. T 1 x. T, M-1 … u 0(t) u 1(t) u. M-1(t) Transmitter emits incoherent waveforms. Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 14

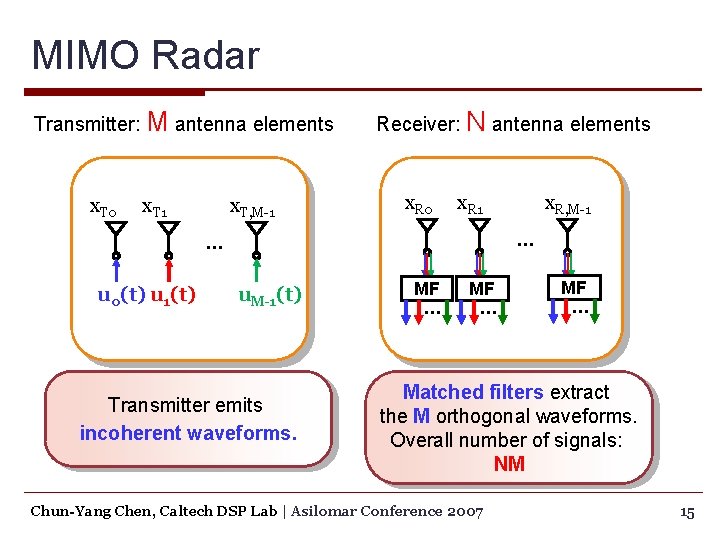
MIMO Radar Transmitter: M antenna elements x. T 0 x. T 1 x. T, M-1 Receiver: N antenna elements x. R 0 x. R 1 … … u 0(t) u 1(t) x. R, M-1 u. M-1(t) Transmitter emits incoherent waveforms. MF … Matched filters extract the M orthogonal waveforms. Overall number of signals: NM Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 15

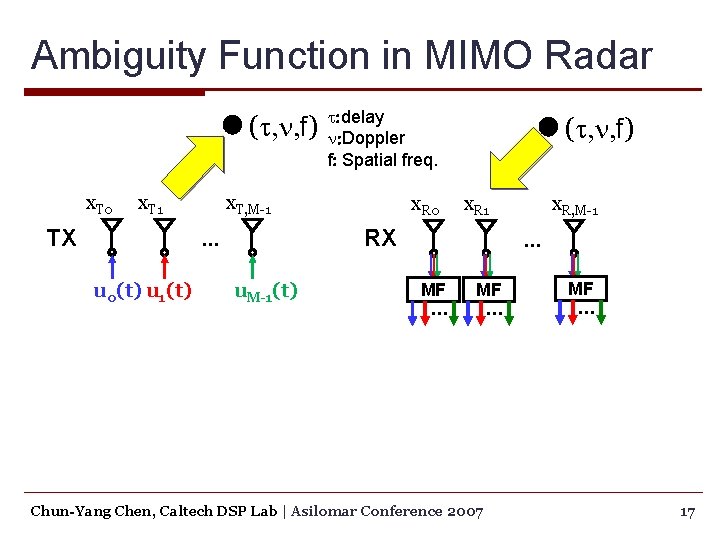
Ambiguity Function in MIMO Radar (t, n, f) t: delay x. T 0 x. T 1 TX x. T, M-1 n: Doppler f: Spatial freq. … u 0(t) u 1(t) u. M-1(t) Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 16

Ambiguity Function in MIMO Radar (t, n, f) x. T 0 x. T 1 TX x. T, M-1 x. R 0 (t, n, f) x. R 1 RX … u 0(t) u 1(t) t: delay n: Doppler f: Spatial freq. u. M-1(t) x. R, M-1 … MF … Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 MF … 17

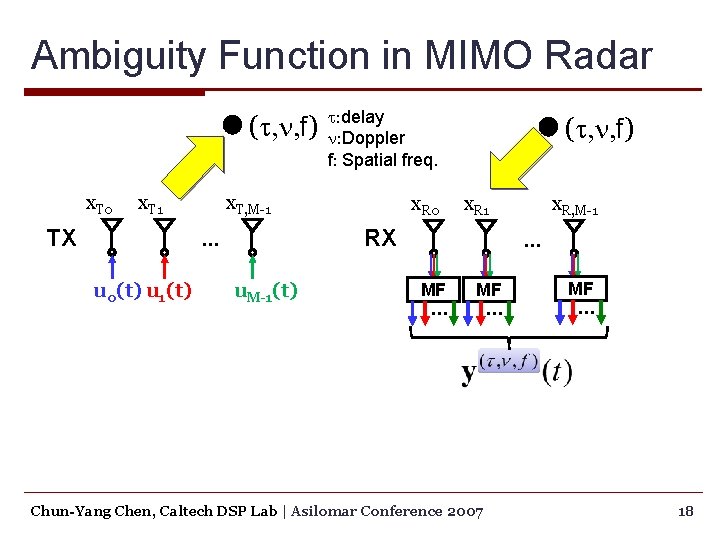
Ambiguity Function in MIMO Radar (t, n, f) x. T 0 x. T 1 TX x. T, M-1 x. R 0 (t, n, f) x. R 1 RX … u 0(t) u 1(t) t: delay n: Doppler f: Spatial freq. u. M-1(t) x. R, M-1 … MF … Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 MF … 18

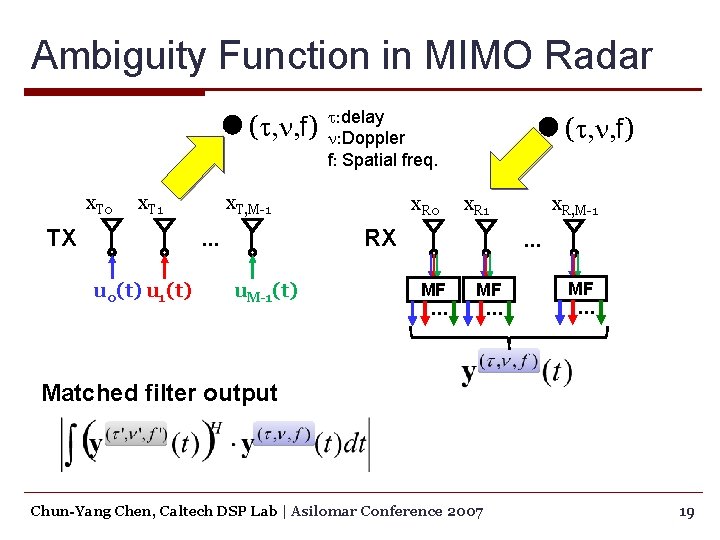
Ambiguity Function in MIMO Radar (t, n, f) x. T 0 x. T 1 TX x. T, M-1 x. R 0 (t, n, f) x. R 1 RX … u 0(t) u 1(t) t: delay n: Doppler f: Spatial freq. u. M-1(t) x. R, M-1 … MF … Matched filter output Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 19

Ambiguity Function in MIMO Radar Matched filter output t: delay n: Doppler f: Spatial freq. um(t): m-th waveform xm: m-th antenna location n: receiving antenna index Receiver beamforming Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 20

Ambiguity Function in MIMO Radar Matched filter output t: delay n: Doppler f: Spatial freq. um(t): m-th waveform xm: m-th antenna location n: receiving antenna index Receiver beamforming Cross ambiguity function Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 21

Ambiguity Function in MIMO Radar Matched filter output t: delay n: Doppler f: Spatial freq. um(t): m-th waveform xm: m-th antenna location n: receiving antenna index Receiver beamforming [San Antonio et al. 07] MIMO ambiguity function Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 22

Ambiguity Function in MIMO Radar § Ambiguity function characterizes the Doppler, range, and angular resolution. n target 1 (t 1, n 1, f 1) target 2 (t 2, n 2, f 2) t f Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 23

Ambiguity Function in MIMO Radar § Ambiguity function characterizes the Doppler, range, and angular resolution. n target 1 (t 1, n 1, f 1) target 2 (t 2, n 2, f 2) t f Ambiguity function Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 24

2 Proposed Waveform Design Method 25

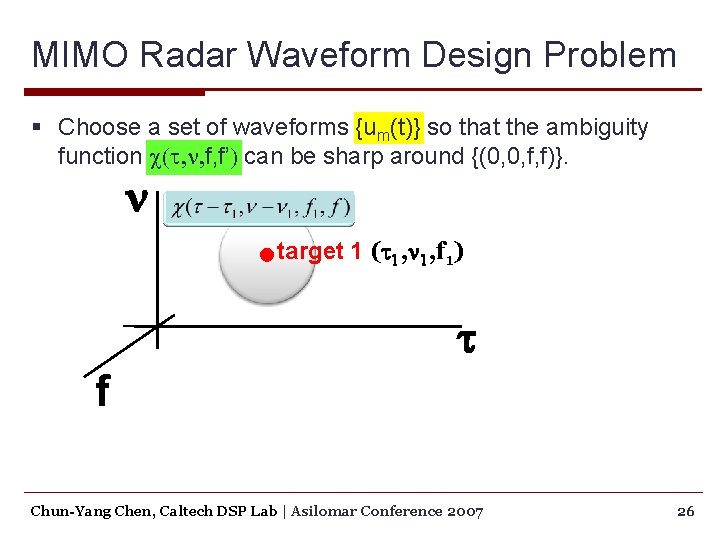
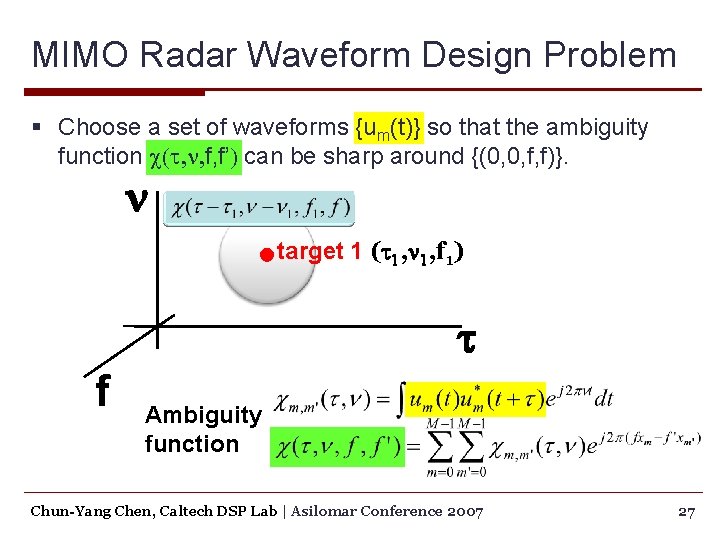
MIMO Radar Waveform Design Problem § Choose a set of waveforms {um(t)} so that the ambiguity function c(t, n, f, f’) can be sharp around {(0, 0, f, f)}. n target 1 (t 1, n 1, f 1) t f Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 26

MIMO Radar Waveform Design Problem § Choose a set of waveforms {um(t)} so that the ambiguity function c(t, n, f, f’) can be sharp around {(0, 0, f, f)}. n target 1 (t 1, n 1, f 1) t f Ambiguity function Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 27

Imposing Waveform Structures § Pulse radar m-th waveform – MTI (Moving Target Indicator) – Doppler pulse radar Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 28

Imposing Waveform Structures § Pulse radar m-th waveform – MTI (Moving Target Indicator) – Doppler pulse radar § Frequency hopping signals – Constant modulus – Can be viewed as generalized LFM (Linear Frequency Modulation) Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 29

Imposing Waveform Structures § Pulse radar m-th waveform – MTI (Moving Target Indicator) – Doppler pulse radar § Frequency hopping signals – Constant modulus – Can be viewed as generalized LFM (Linear Frequency Modulation) § Orthogonal waveforms – Virtual array Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 30

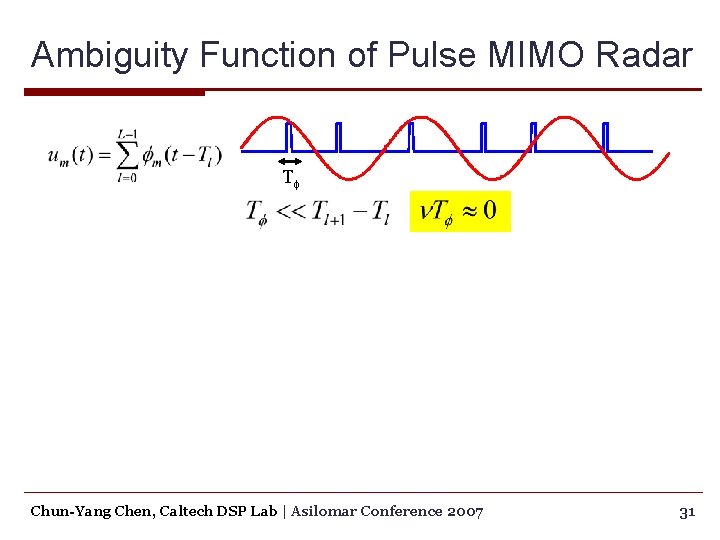
Ambiguity Function of Pulse MIMO Radar Tf Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 31

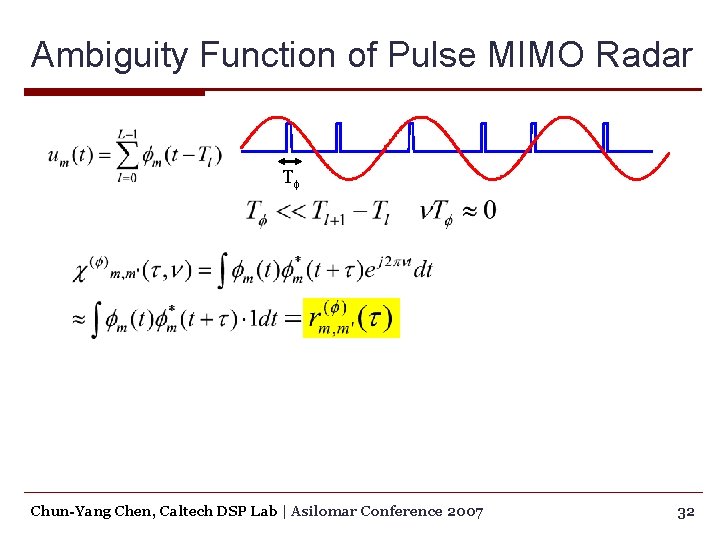
Ambiguity Function of Pulse MIMO Radar Tf Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 32

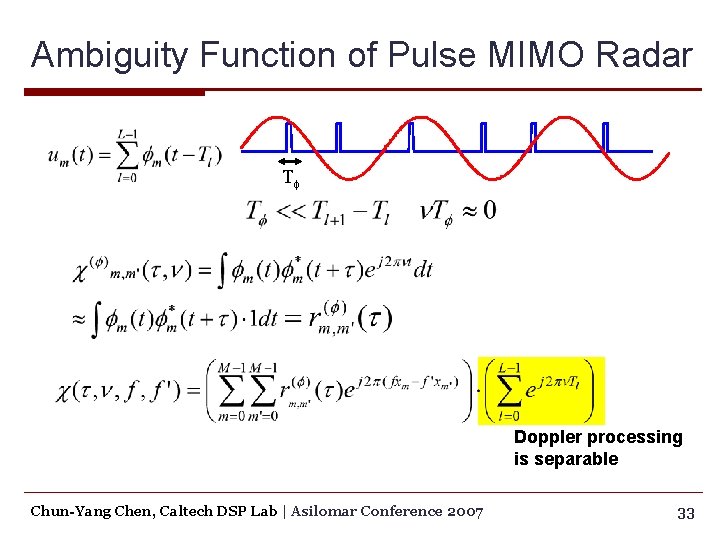
Ambiguity Function of Pulse MIMO Radar Tf Doppler processing is separable Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 33

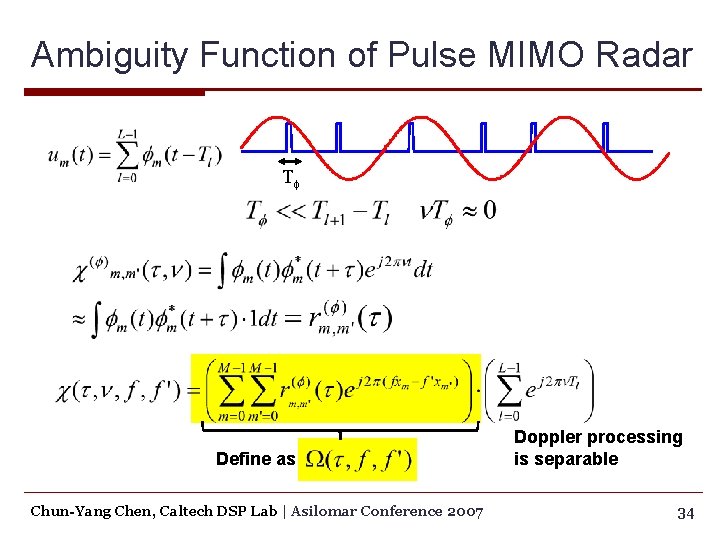
Ambiguity Function of Pulse MIMO Radar Tf Define as Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 Doppler processing is separable 34

Waveform Design Problem in Pulse MIMO Radar Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 35

Waveform Design Problem in Pulse MIMO Radar § Choose a set of pulses {fm(t)} such that W(t, f, f’) can be sharp around {(0, f, f)}. Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 36

Waveform Design Problem in Pulse MIMO Radar § Choose a set of pulses {fm(t)} such that W(t, f, f’) can be sharp around {(0, f, f)}. § Ex: SIMO case: M=1 Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 37

Waveform Design Problem in Pulse MIMO Radar § Choose a set of pulses {fm(t)} such that W(t, f, f’) can be sharp around {(0, f, f)}. § Ex: SIMO case: M=1 Choose a pulse with a sharp correlation function (e. g. LFM) Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 38

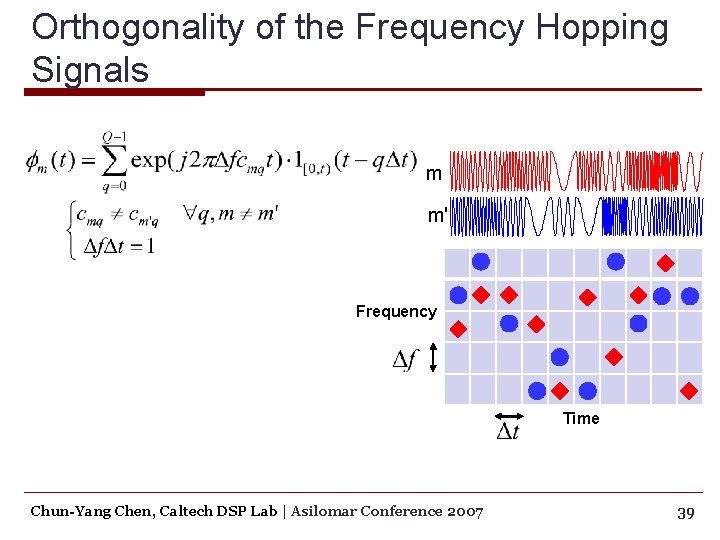
Orthogonality of the Frequency Hopping Signals m m' Frequency Time Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 39

Orthogonality of the Frequency Hopping Signals m m' Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 40

Orthogonality of the Frequency Hopping Signals m m' Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 41

Orthogonality of the Frequency Hopping Signals m m' § W is a constant along {(0, f, f)}, no matter what codes are chosen. Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 42

Optimization of the Codes § Define a vector Code C is better than code C’. Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 43

Optimization of the Codes § Define a vector Code C is better than code C’. § Def: a code C is efficient if there exists no other code C’ such that Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 44

Optimization of the Codes § Define a vector Code C is better than code C’. § Def: a code C is efficient if there exists no other code C’ such that § For any functions where gi are increasing convex Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 45

Optimization of the Codes § Define a vector Code C is better than code C’. § Def: a code C is efficient if there exists no other code C’ such that § For any functions where gi are increasing convex § So a code C is efficient if for all C’. Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 46

Optimization of the Codes § Define a vector Code C is better than code C’. § Def: a code C is efficient if there exists no other code C’ such that § For any functions where gi are increasing convex § So a code C is efficient if § Example: Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 for all C’. 47

Optimization of the Codes M: # of waveforms Q: # of freq. hops K: # of freq. Time-bandwidth product: KDf. QDt Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 48

Simulated Annealing Algorithm subject to § Simulated annealing [S. Kirkpatrick et al. 85] – Create a Markov chain on the set A C’ C … … Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 49

Simulated Annealing Algorithm subject to § Simulated annealing [S. Kirkpatrick et al. 85] – Create a Markov chain on the set A with the equilibrium distribution C’ C … … Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 50

Simulated Annealing Algorithm subject to § Simulated annealing [S. Kirkpatrick et al. 85] – Create a Markov chain on the set A with the equilibrium distribution C’ C … … – Run the Markov chain Monte Carlo (MCMC) Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 51

Simulated Annealing Algorithm subject to § Simulated annealing [S. Kirkpatrick et al. 85] – Create a Markov chain on the set A with the equilibrium distribution C’ C … … – Run the Markov chain Monte Carlo (MCMC) – Decrease the temperature T from time to time Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 52

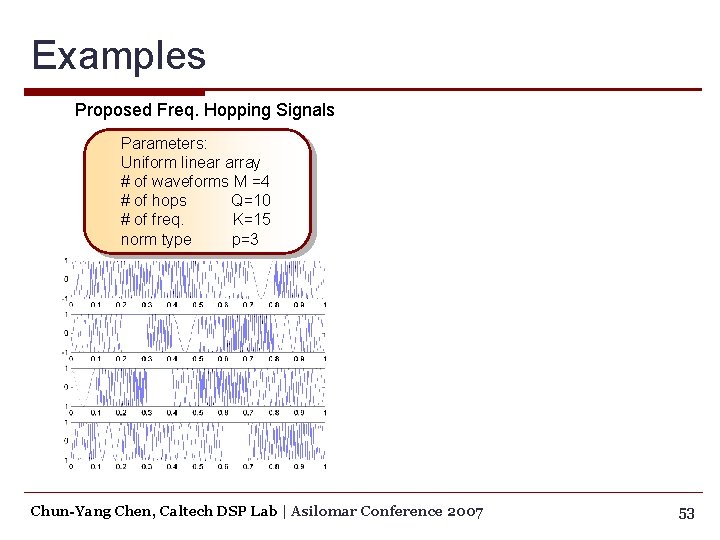
Examples Proposed Freq. Hopping Signals Parameters: Uniform linear array # of waveforms M =4 # of hops Q=10 # of freq. K=15 norm type p=3 Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 53

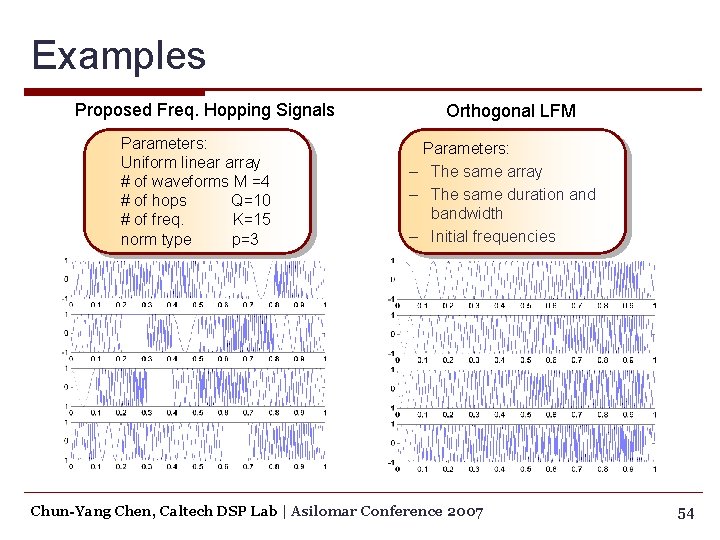
Examples Proposed Freq. Hopping Signals Parameters: Uniform linear array # of waveforms M =4 # of hops Q=10 # of freq. K=15 norm type p=3 Orthogonal LFM Parameters: – The same array – The same duration and bandwidth – Initial frequencies Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 54

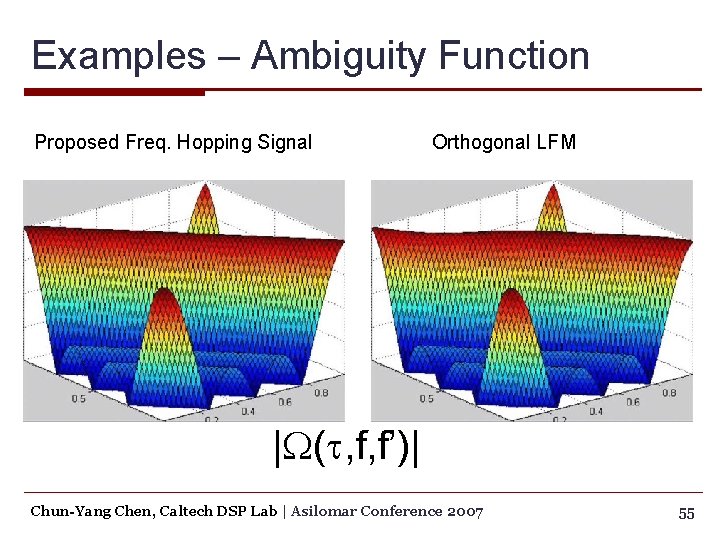
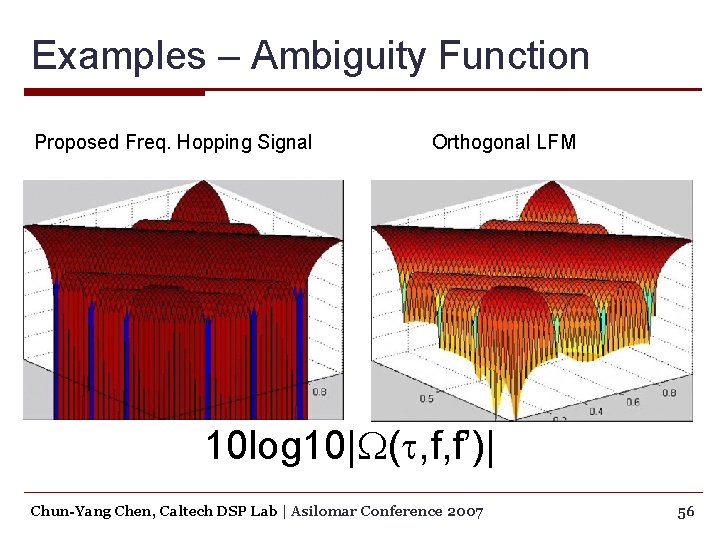
Examples – Ambiguity Function Proposed Freq. Hopping Signal Orthogonal LFM |W(t, f, f’)| Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 55

Examples – Ambiguity Function Proposed Freq. Hopping Signal Orthogonal LFM 10 log 10|W(t, f, f’)| Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 56

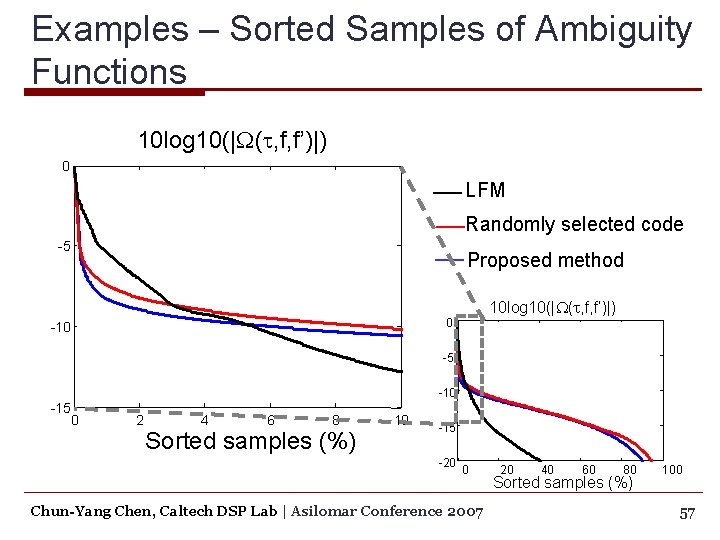
Examples – Sorted Samples of Ambiguity Functions 10 log 10(|W(t, f, f’)|) 0 LFM Randomly selected code -5 Proposed method 10 log 10(|W(t, f, f’)|) 0 -10 -5 -10 -15 0 2 4 6 8 Sorted samples (%) 10 -15 -20 0 Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 20 40 60 80 Sorted samples (%) 100 57

Examples – Correlation Function Matrix Proposed Freq. Hopping Signal Orthogonal LFM Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 58

Conclusion § MIMO radar frequency hopping waveform design method – Sharper ambiguity function (Better resolution) – Applicable in the case of • pulse radar • orthogonal waveforms § Future work – Other optimization tools – Phase coded signals Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 59

Thank You! Q&A Any questions? Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007 60