A Data Parallel Algorithm for Seismic Raytracing Allen

A Data Parallel Algorithm for Seismic Raytracing Allen D. Malony 1, Stephanie Mc. Cumsey 1, Joseph Byrnes 2 Craig Rasmusen 3, Soren Rasmusen 4, Erik Keever 3, Doug Toomey 2 1 Dept. Computer and Information Science 2 Dept. Geological Science 3 Dept. Physics 4 Neuroinformactics Center University of Oregon

Marine Seismology q q Mid-ocean ridges transfer heat and material from Earth’s interior to its surface Much of the planet’s generation of magma occurs at these ridges each year ❍ q 20 km 3 of new oceanic crust is formed as magma rises up from the mantle to form seafloor volcanoes Marine geologists use seismic tomography to study the geophysical properties of ocean floor and structures below Seismic waves propagate through the Earth at a velocity that varies with temperature, composition, and presence of magma ❍ Seismic velocities are sensitive to elastic anisotropy, temperature, presence of partial melt, and variations in porosity ❍ q By constructing 3 D models of the seismic velocity at points in the crust and underlying mantle, the geologist can infer magmatic, hydrothermal, and tectonic processes involved Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Seismic Raytracing and Tomography q Seismic tomography works by measuring the arrival times of seismic waves from a source of seismic radiation ❍ q q Experiments at sea Compare the observed arrival times to predictive arrival times using a starting model Seismic raytracing calculates wave arrival times using Forward problem with model ❍ Single-source shortest-path ❍ q Seismic tomography is an ill-posed problem Inversion problem perturbs starting model to minimize misfit ❍ Reverse Time migration (RTM) inversion ❍ Full Wave Inversion (FWI) inversion ❍ Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Single Source Shortest Path (SSSP) q q A common problem in computing is finding the shortest path from a single source to all other points in a graph Dijkstra’s 1959 paper, “A Note on Two Problems in Connexion with Graphs, ” describes his famous algorithm Given a graph of n nodes each with cost on each edge e and a starting node s, find a path of minimum cost to s for each node ❍ Grow a tree with s at the root, adding at each step an unassigned vertex and edge which minimizes a shortest path from v to s ❍ Dijkstra’s algorithm is inherently serial ❍ q Bellman-Ford-Moore’s 1959 algorithm for SSSP updates each vertex based on neighbors’ estimates of shortest path Multiple iterations are required to reach a converged state ❍ But it exposes opportunities for (data) parallelism ❍ Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Moser’s Seismic Raytracing q q Moser (1991) formulated seismic raytracing based on Dijkstra Represented the seismic velocity of a region of the Earth as: ❍ ❍ 3 D grid of Nx x Ny x Nz points Each point connect to all neighbor points of radius R (forward star) Finds shortest path from starting point s to all other points in model Moser algorithm (implemented by Toomey in Stingray): 1) Initialize travel time to starting point s at all points to ∞ and s to 0 q ❍ A seismometer “receiver” is the starting point here 2) Run Dijkstra’s algorithm starting point forward star Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Data Parallel Seismic Raytracing q q q Can reformulate the seismic raytracing problem as an iterative constraint convergence problem using BFM Let V be the velocity field and T the travel times from each grid point p to a starting point s If the final travel times are known for each model point p, T(p), they must satisfy the constraint: q Thus, an iterative procedure can be specified as: q This is guaranteed to converge to correct travel times Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Parallelization Design Strategy q Seismic raytracing with BFM algorithm is highly parallel Excellent opportunity for parallelization ❍ Multicore CPUs and manycore coprocessors ❍ q q Would like to articulate a parallelization design model that could map to different execution targets Decompose the model domain into rectangular regions that can be worked on in parallel at each iteration step Regions defined to are non-overlapping ❍ Eliminate dependencies between regions ❍ Requires exchanges between neighbor regions to update the travel times for points on the region boundaries ❍ q Standard domain decomposition approach with halos used for exchanging boundary data Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

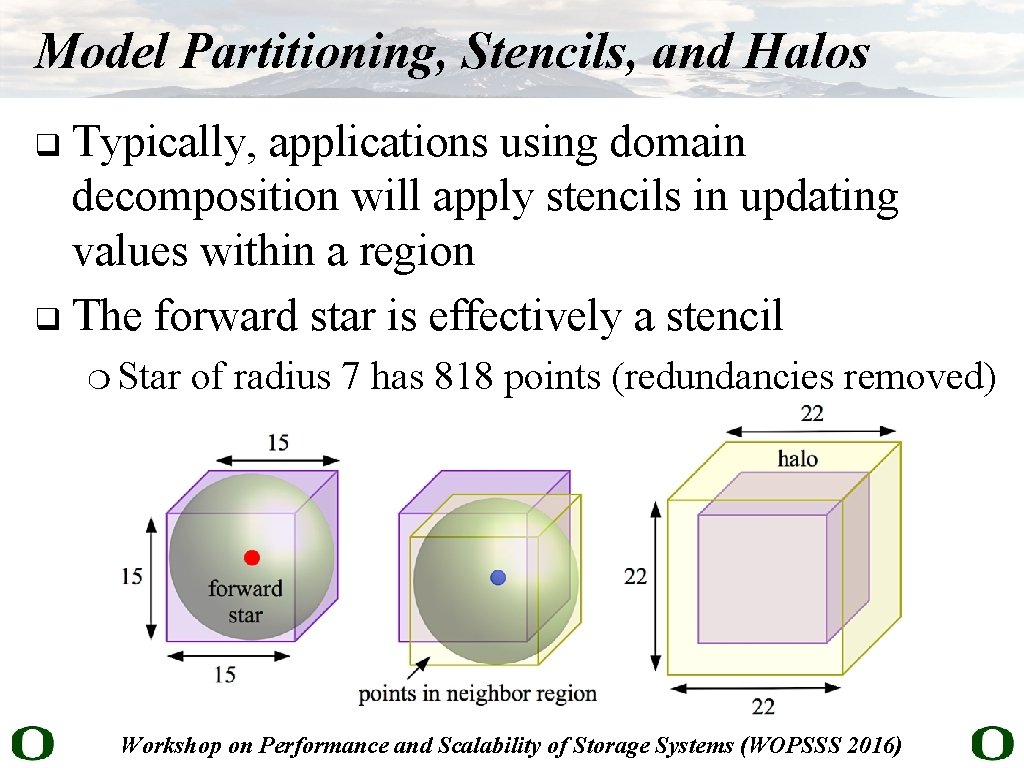
Model Partitioning, Stencils, and Halos Typically, applications using domain decomposition will apply stencils in updating values within a region q The forward star is effectively a stencil q ❍ Star of radius 7 has 818 points (redundancies removed) Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

BFM (ICC) Update Method q At each step, each model point is updated Could be done simultaneously (2 copies of model data) ❍ Instead try to use the model in place ❍ q Need point update schedule Inspired by alternate direction implicit (ADI) methods ❍ Helps to determine parallelization schedule ❍ Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Optimization in Forward Star Updates Each model point p is updated at each step with a smaller travel time to the starting point s, based on the delays calculated in its forward star, FS(p) q It is possible to perform another local test and possible update to the travel times of points q in FS(p) during the update process: q

Implementation Approach q Stingray-DSP (Moser algorithm) Sequential Fortran (F 90) implementation of Moser ❍ Run on single starting point (replicate for multiple) ❍ q Stingray-ICC-multistart (ICC algorithm) C with Open. MP ❍ Each thread runs sequentially for a single starting point ❍ q Stingray-ICC-parsingle (ICC algorithm) C with Open. MP ❍ Parallelize for a single starting point ❍ q Stingray-ICC-gpu (ICC algorithm) Co-array Fortran extensions (CAFe) with Open. CL kernels ❍ CAFe translation to Fortran with calls to Open. CL C library ❍ Parallelize for a single starting point ❍ Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

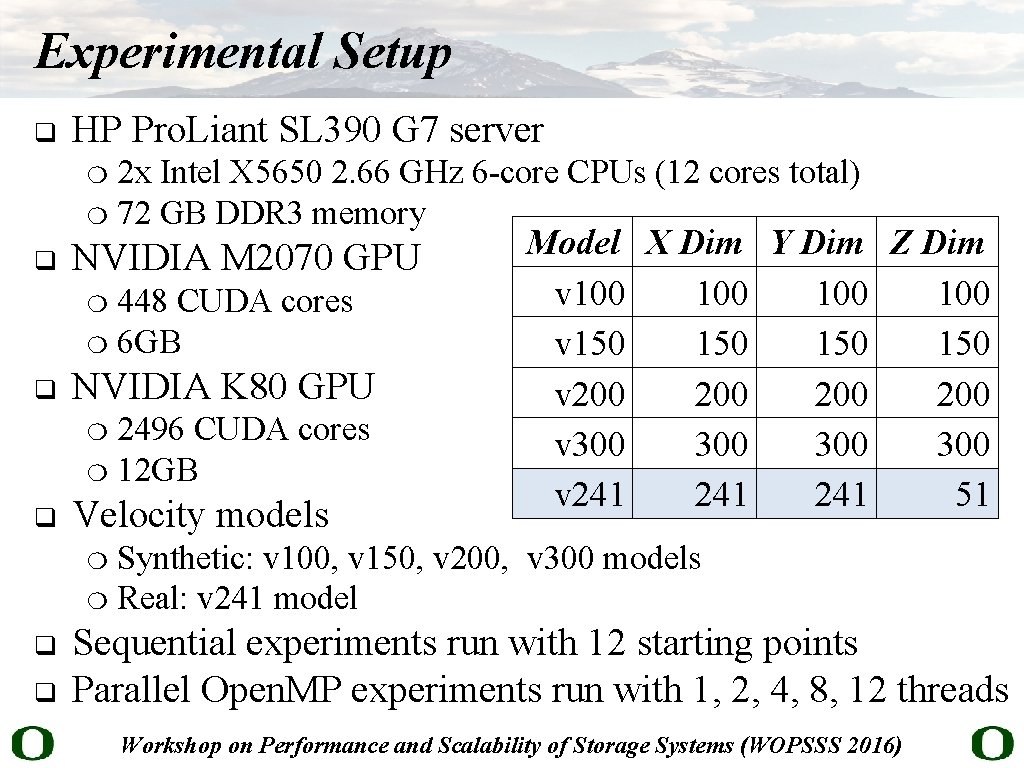
Experimental Setup q HP Pro. Liant SL 390 G 7 server 2 x Intel X 5650 2. 66 GHz 6 -core CPUs (12 cores total) ❍ 72 GB DDR 3 memory ❍ q NVIDIA M 2070 GPU 448 CUDA cores ❍ 6 GB ❍ q NVIDIA K 80 GPU 2496 CUDA cores ❍ 12 GB ❍ q Velocity models Model X Dim Y Dim Z Dim v 100 100 v 150 150 v 200 200 v 300 300 v 241 241 51 Synthetic: v 100, v 150, v 200, v 300 models ❍ Real: v 241 model ❍ q q Sequential experiments run with 12 starting points Parallel Open. MP experiments run with 1, 2, 4, 8, 12 threads Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Performance Results q q DSP is O(n 3) and scales as (Nx*Ny*Nz)/7500 sec for HP ICC is faster overall Open. MP (seq): ~2. 5 x faster ❍ GPU (1 start): ~15 x faster ❍ Sequential (average) q q Stingray-ICC serial is an average of 12 starting points Parallelization time affected by convergence rate ❍ Time per sweep decreases Synthetic Real 30 61 21 41 47 7 Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016) 53

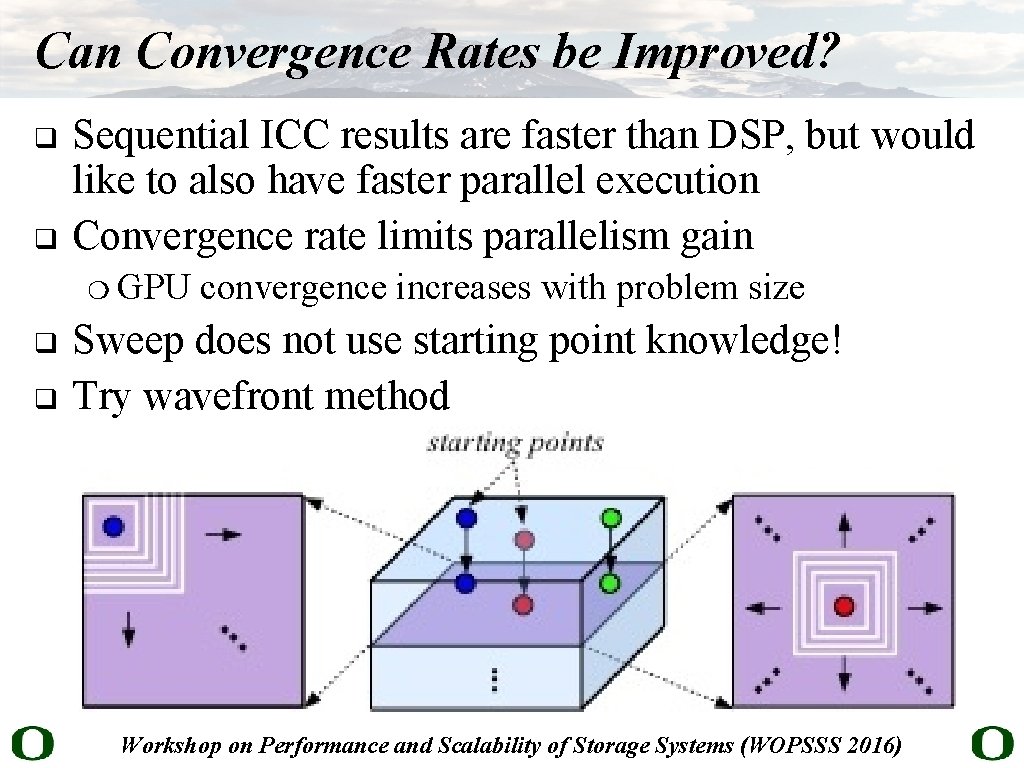
Can Convergence Rates be Improved? q q Sequential ICC results are faster than DSP, but would like to also have faster parallel execution Convergence rate limits parallelism gain ❍ q q GPU convergence increases with problem size Sweep does not use starting point knowledge! Try wavefront method Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Wavefront Method with Open. MP Test with 241 x 51 real problem q Knowledge of starting point allows updates to propagate more rapidly, improving performance q Convergence rates continue to increase (not as fast) q # Threads Time (sec) # Wavefronts Time/Wavefront 1 109. 30 5 21. 86 2 64. 30 5 12. 86 4 56. 67 8 6. 46 6 48. 70 11 4. 43 8 50. 65 15 3. 38 10 41. 33 15 2. 76 12 23. 99 10 2. 31 Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Larger Problems q There is a strong interest in working on problems of larger size (up to 10 x in each dimension) ❍ q Higher resolution and greater scale Problems Larger size problems could overwhelm memory ❍ Increasing turnaround time ❍ ◆964 x 204 (64 x) takes 25, 277 seconds with DSP ◆need to continue to get benefits from parallelism q Need to develop distributed memory implementations to manage larger data and faster time to solution Prototype of MPI+Open. MP implementation ❍ Must return to using the sweep method ❍ Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

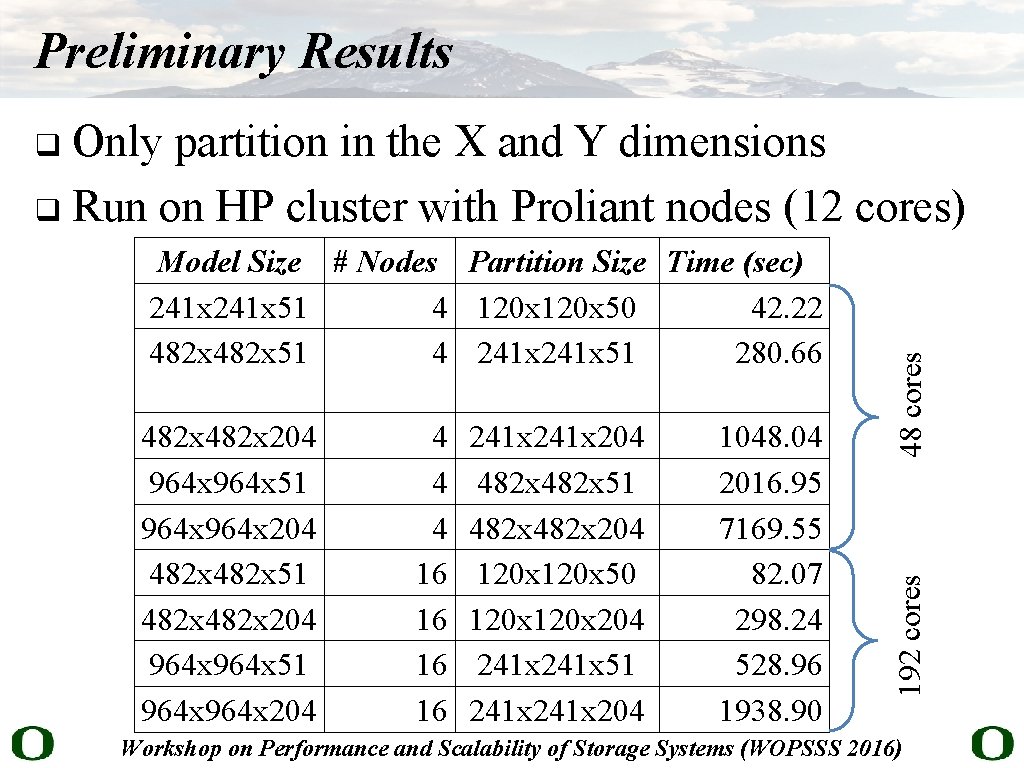
Preliminary Results Only partition in the X and Y dimensions q Run on HP cluster with Proliant nodes (12 cores) 482 x 204 964 x 51 964 x 204 482 x 51 482 x 204 964 x 51 964 x 204 4 16 16 241 x 204 482 x 51 482 x 204 120 x 50 120 x 204 241 x 51 241 x 204 1048. 04 2016. 95 7169. 55 82. 07 298. 24 528. 96 1938. 90 192 cores Model Size # Nodes Partition Size Time (sec) 241 x 51 4 120 x 50 42. 22 482 x 51 4 241 x 51 280. 66 48 cores q Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

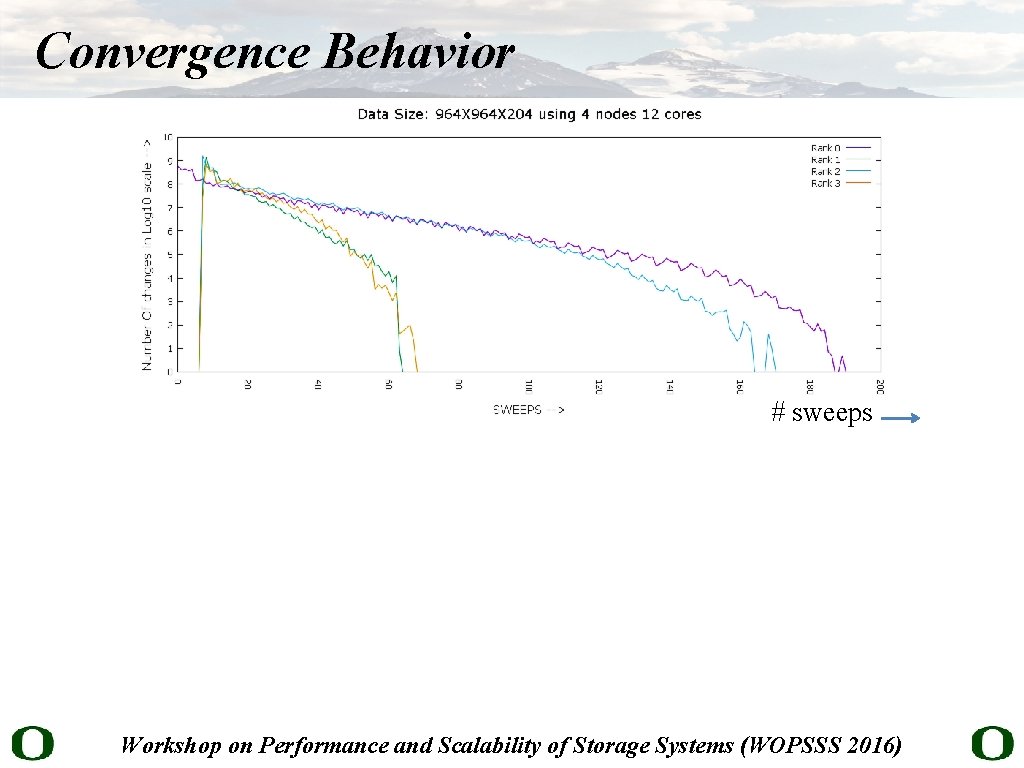
Convergence Behavior # sweeps Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Conclusions and Future Work q Data parallel algorithm for seismic raytracing based on BFM outperforms Moser’s DSP method Sequential execution is faster ❍ Parallelism with Open. MP and GPU (Open. CL) ❍ q q q Identified issues associated with convergence Integration of multiple starting points Extend to support shearing and anisotropy ❍ q Develop new distributed memory implementations ❍ q Affects only the forward star computation time MPI+GPU using CUDA and MPI+Phi using Open. MP Go after very large models ❍ 5 k x 5 k problem (1000 500 x 500 partitions) Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)

Workshop on Performance and Scalability of Storage Systems (WOPSSS 2016)