A Data Compression Algorithm Huffman Compression Gordon College

A Data Compression Algorithm: Huffman Compression Gordon College 1

2 Aaa aaa aa a a a aa aa aaaa a a a a a aa aa aaaa aa aa aaaa aa aa aaaa aaaa aa Uncompress Aaa aa aa aaa aa a Aaa aa aa aaa aa a Aaa aaa aa a Aaa aa aa aaa aa a a a aa aa aaaa Aaa aaa aa aa aaaa Compress Aaa aaa aa a a a aa aa aaaa Aaa aa Aaa aa Aaa aa aa aa aaa aaa aaa aaa aa aa aa a a a a a a a a aa aa aa aa aa aa aaaa aaaa aaaa aaaa • Definition: process of encoding which uses fewer bits • Reason: to save valuable resources such as communication bandwidth or hard disk space Compression

Compression Types 1. Lossy – Loses some information during compression which means the exact original can not be recovered (jpeg) – Normally provides better compression – Used when loss is acceptable - image, sound, and video files 3

Compression Types 1. Lossless – exact original can be recovered – usually exploit statistical redundancy – Used when loss is not acceptable - data Basic Term: Compression Ratio - ratio of the number of bits in original data to the number of bits in compressed data For example: 3: 1 is when the original file was 3000 bytes and the compression file is now only 1000 bytes. 4

Variable-Length Codes • Recall that ASCII, EBCDIC, and Unicode use same size data structure for all characters • Contrast Morse code – Uses variable-length sequences • The Huffman Compression is a variable-length encoding scheme 5

Variable-Length Codes • Each character in such a code – Has a weight (probability) and a length • The expected length is the sum of the products of the weights Goal and lengths for all the characters minimize the expected length 0. 2 x 2 + 0. 1 x 4 + 0. 15 x 3 + 0. 45 x 1 = 2. 1 6

Huffman Compression • Uses prefix codes (sequence of optimal binary codes) • Uses a greedy algorithm - looks at the data at hand makes a decision based on the data at hand. 7

Huffman Compression Basic algorithm 1. Generates a table that contains the frequency of each character in a text. 2. Using the frequency table - assign each character a “bit code” (a sequence of bits to represent the character) 3. Write the bit code to the file instead of the character. 8

Immediate Decodability • Definition: When no sequence of bits that represents a character is a prefix of a longer sequence for another character Purpose: Can be decoded without waiting for remaining bits • Coding scheme to the right is not immediately decodable • However this one is 9

Huffman Compression • Huffman (1951) • Uses frequencies of symbols in a string to build a variable rate prefix code. – Each symbol is mapped to a binary string. – More frequent symbols have shorter codes. – No code is a prefix of another. t o N ff u H n ma es d o C 10

Huffman Codes • We seek codes that are – Immediately decodable – Each character has minimal expected code length • For a set of n characters { C 1. . Cn } with weights { w 1. . wn } – We need an algorithm which generates n bit strings representing the codes 11

Cost of a Huffman Tree • Let p 1, p 2, . . . , pm be the probabilities for the symbols a 1, a 2, . . . , am, respectively. • Define the cost of the Huffman tree T to be where ri is the length of the path from the root to ai. • HC(T) is the expected length of the code of a symbol coded by the tree T. HC(T) is the bit rate of the code. 12

Example of Cost • Example: a 1/2, b 1/8, c 1/8, d 1/4 HC(T) = 1 x 1/2 + 3 x 1/8 + 2 x 1/4 = 1. 75 a b c d 13

Huffman Tree • Input: Probabilities p 1, p 2, . . . , pm for symbols a 1, a 2, . . . , am, respectively. • Output: A tree that minimizes the average number of bits (bit rate) to code a symbol. That is, minimizes where ri is the length of the path from the root to ai. This is a Huffman tree or Huffman code. 14

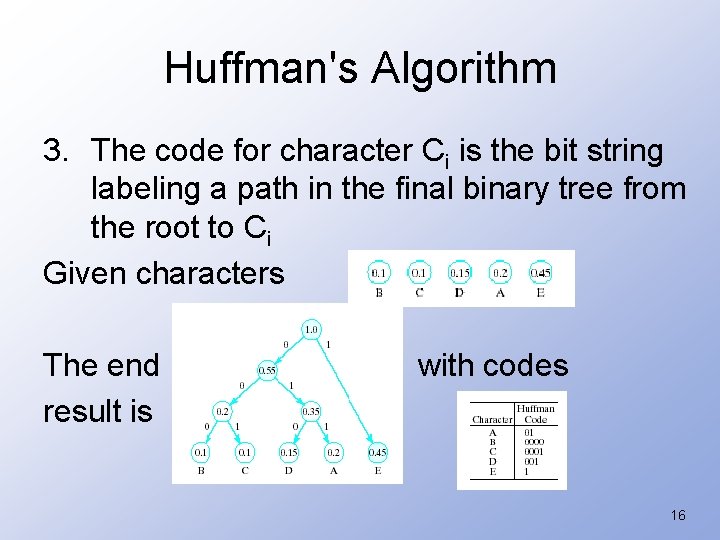
Recursive Algorithm - Huffman Codes 1. Initialize list of n one-node binary trees containing a weight for each character 2. Repeat the following n – 1 times: a. Find two trees T' and T" in list with minimal weights w' and w" b. Replace these two trees with a binary tree whose root is w' + w" and whose subtrees are T' and T" and label points to these subtrees 0 and 1 15

Huffman's Algorithm 3. The code for character Ci is the bit string labeling a path in the final binary tree from the root to Ci Given characters The end result is with codes 16

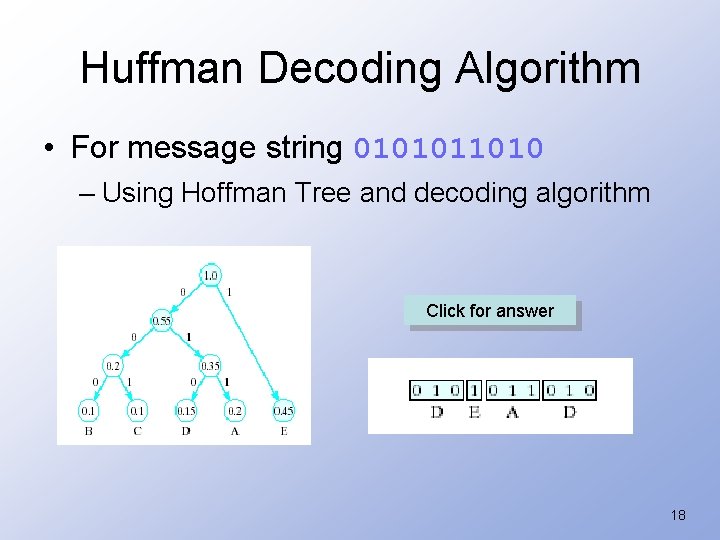
Huffman Decoding Algorithm 1. Initialize pointer p to root of Huffman tree 2. While end of message string not reached repeat the following: a. Let x be next bit in string b. if x = 0 set p equal to left child pointer else set p to right child pointer c. If p points to leaf i. Display character with that leaf ii. Reset p to root of Huffman tree 17

Huffman Decoding Algorithm • For message string 0101011010 – Using Hoffman Tree and decoding algorithm Click for answer 18

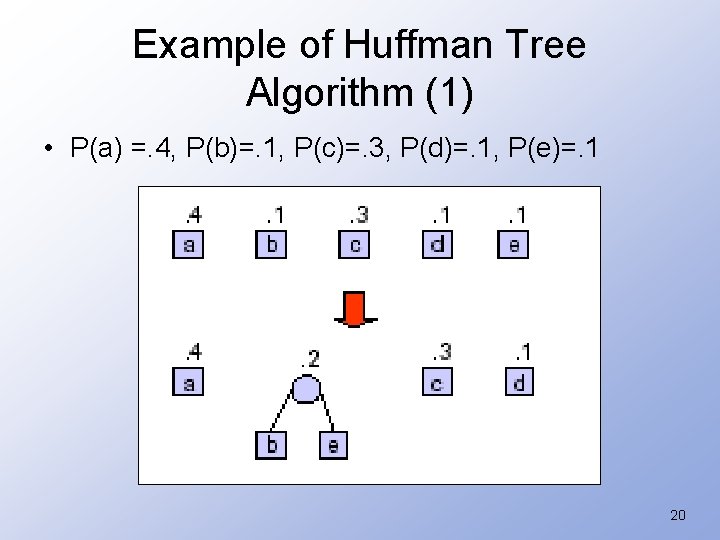
Iterative Huffman Tree Algorithm 1. Form a node for each symbol ai with weight pi; 2. Insert the nodes in a min priority queue ordered by probability; 3. While the priority queue has more than one element do – – – – min 1 : = delete-min; min 2 : = delete-min; create a new node n; n. weight : = min 1. weight + min 2. weight; n. left : = min 1; also associate this link with bit 0 n. right : = min 2; also associate this link with bit 1 insert(n) 4. Return the last node in the priority queue. 19

Example of Huffman Tree Algorithm (1) • P(a) =. 4, P(b)=. 1, P(c)=. 3, P(d)=. 1, P(e)=. 1 20

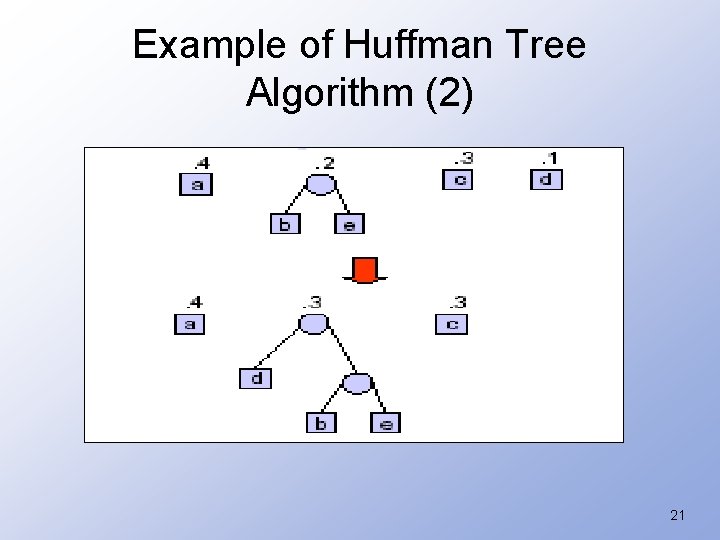
Example of Huffman Tree Algorithm (2) 21

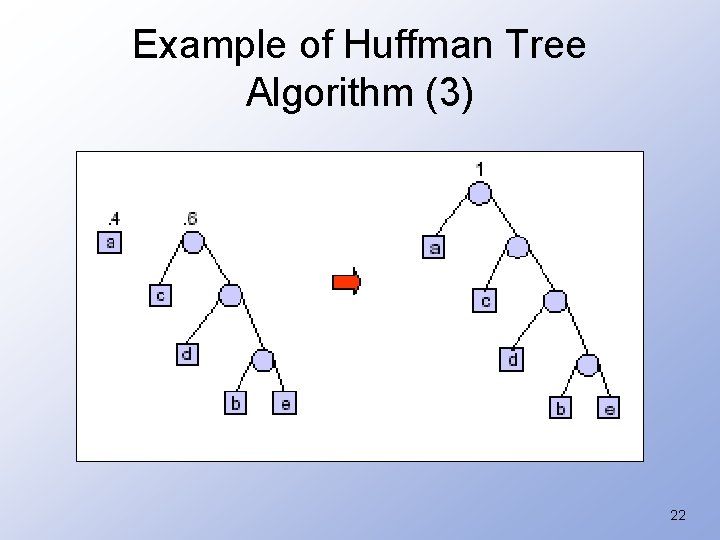
Example of Huffman Tree Algorithm (3) 22

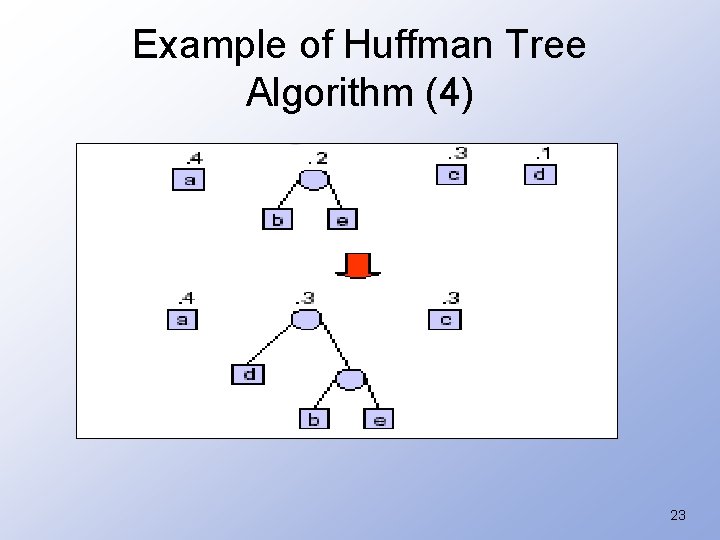
Example of Huffman Tree Algorithm (4) 23

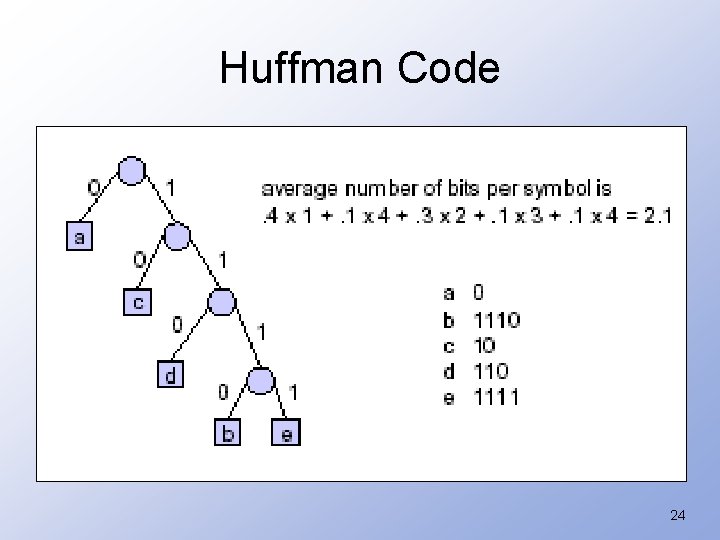
Huffman Code 24

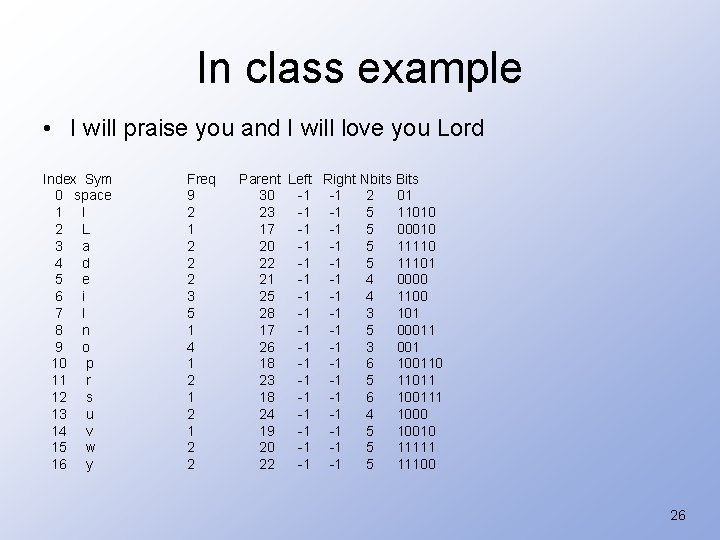
In class example • I will praise you and I will love you Lord Index Sym 0 space 1 I 2 L 3 a 4 d 5 e 6 i 7 l 8 n 9 o 10 p 11 r 12 s 13 u 14 v 15 w 16 y Freq 9 2 1 2 2 2 3 5 1 4 1 2 1 2 2 25

In class example • I will praise you and I will love you Lord Index Sym 0 space 1 I 2 L 3 a 4 d 5 e 6 i 7 l 8 n 9 o 10 p 11 r 12 s 13 u 14 v 15 w 16 y Freq 9 2 1 2 2 2 3 5 1 4 1 2 1 2 2 Parent Left Right Nbits Bits 30 -1 -1 2 01 23 -1 -1 5 11010 17 -1 -1 5 00010 20 -1 -1 5 11110 22 -1 -1 5 11101 21 -1 -1 4 0000 25 -1 -1 4 1100 28 -1 -1 3 101 17 -1 -1 5 00011 26 -1 -1 3 001 18 -1 -1 6 100110 23 -1 -1 5 11011 18 -1 -1 6 100111 24 -1 -1 4 1000 19 -1 -1 5 10010 20 -1 -1 5 11111 22 -1 -1 5 11100 26