A computational study of shear banding in reversible

A computational study of shear banding in reversible associating polymers J. Billen, J. Stegen+, A. R. C. Baljon San Diego State University + Eindhoven University of Technology (The Netherlands) Funded by:

Associating polymers: reversible networks: Outline • • • Molecular dynamics/Monte Carlo simulation Shear banding Shear-induced differences – Shear vs Unshear – High vs Low shear band Sol Temperature Gel

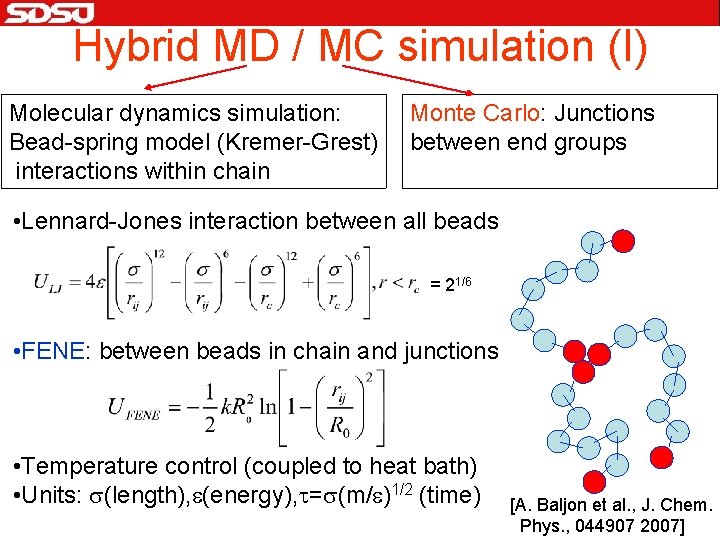
Hybrid MD / MC simulation (I) Molecular dynamics simulation: Bead-spring model (Kremer-Grest) interactions within chain Monte Carlo: Junctions between end groups • Lennard-Jones interaction between all beads = 21/6 • FENE: between beads in chain and junctions • Temperature control (coupled to heat bath) • Units: s(length), e(energy), t=s(m/e)1/2 (time) [A. Baljon et al. , J. Chem. Phys. , 044907 2007]

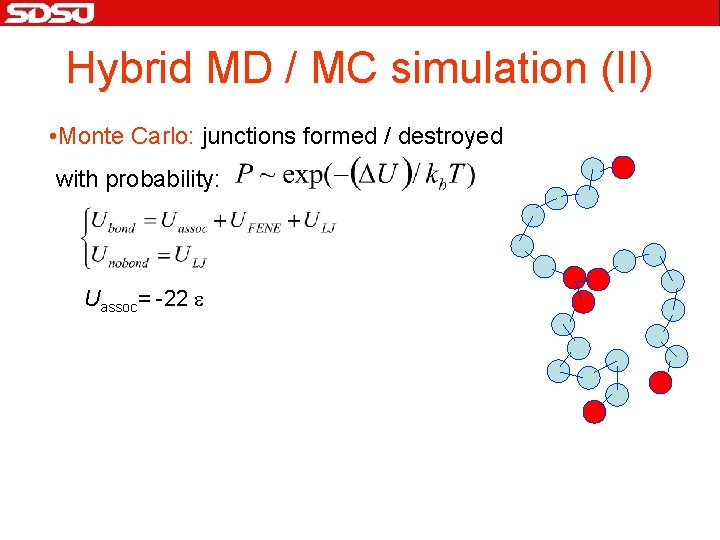
Hybrid MD / MC simulation (II) • Monte Carlo: junctions formed / destroyed with probability: Uassoc= -22 e

Simulation details • 1000 polymeric chains, 8 beads/chain • Box size: (23. 5 x 20. 5 x 27. 9) s 3 with periodic boundary conditions in x/y direction • Concentration = 0. 6 beads / s 3 ( in overlap regime ) • Radius of gyration: = 2. 69 s 2

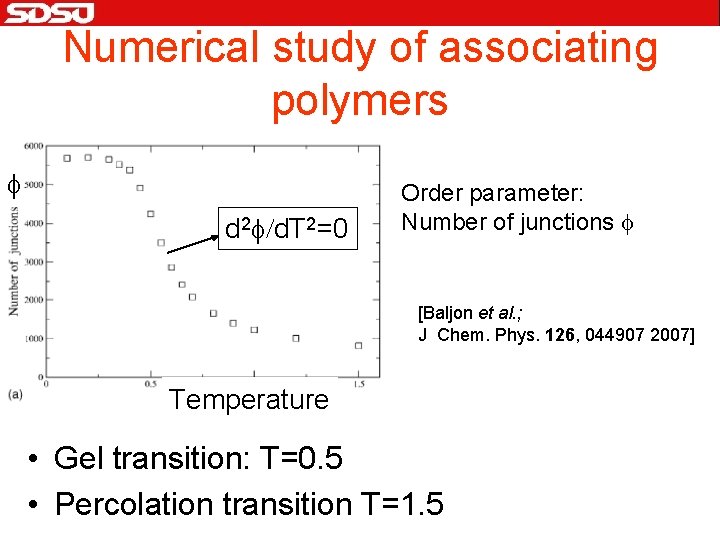
Numerical study of associating polymers f d 2 f/d. T 2=0 Order parameter: Number of junctions f [Baljon et al. ; J Chem. Phys. 126, 044907 2007] Temperature • Gel transition: T=0. 5 • Percolation transition T=1. 5

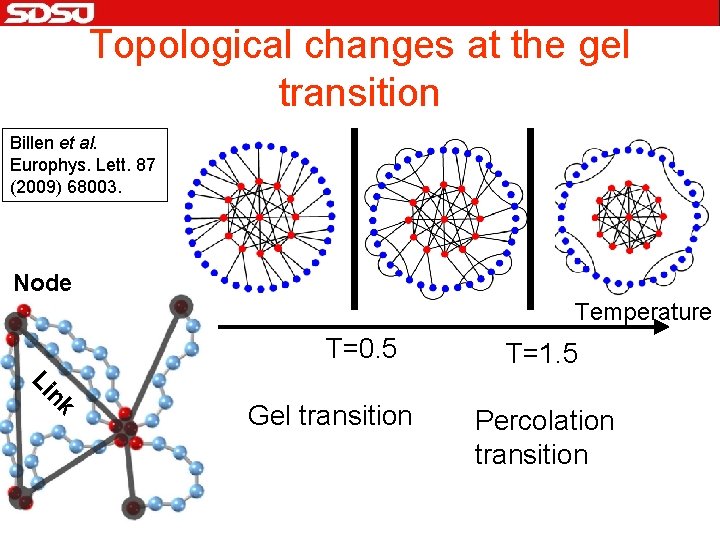
Topological changes at the gel transition Billen et al. Europhys. Lett. 87 (2009) 68003. Node Temperature T=0. 5 nk Li Gel transition T=1. 5 Percolation transition

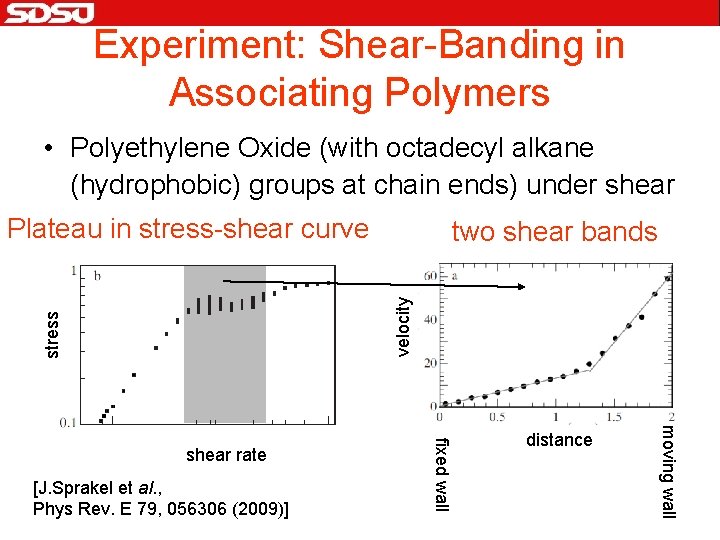
Experiment: Shear-Banding in Associating Polymers • Polyethylene Oxide (with octadecyl alkane (hydrophobic) groups at chain ends) under shear Plateau in stress-shear curve stress velocity two shear bands moving wall [J. Sprakel et al. , Phys Rev. E 79, 056306 (2009)] fixed wall shear rate distance

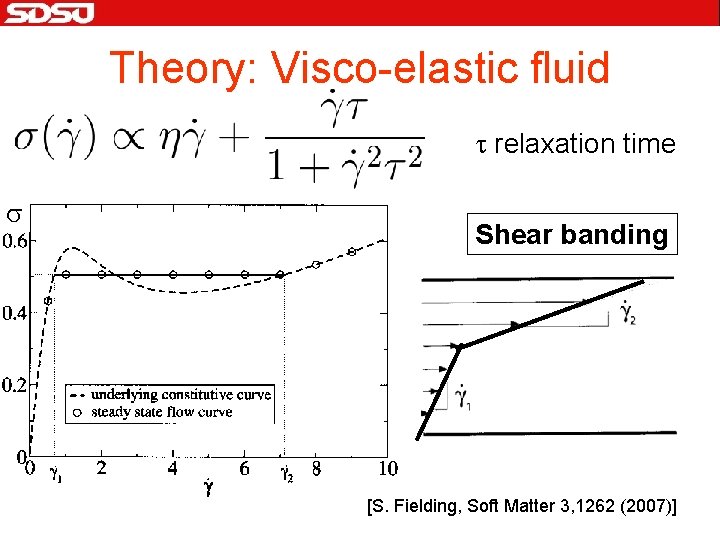
Theory: Visco-elastic fluid t relaxation time s Shear banding [S. Fielding, Soft Matter 3, 1262 (2007)]

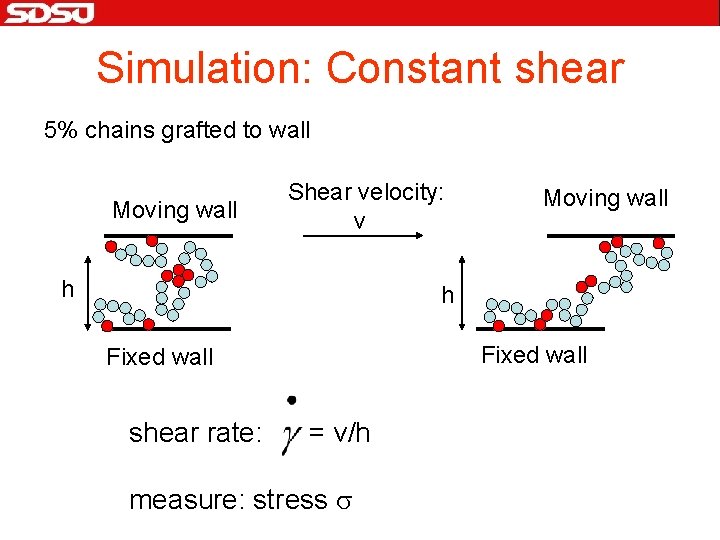
Simulation: Constant shear 5% chains grafted to wall Moving wall Shear velocity: v h Moving wall h Fixed wall shear rate: = v/h measure: stress s

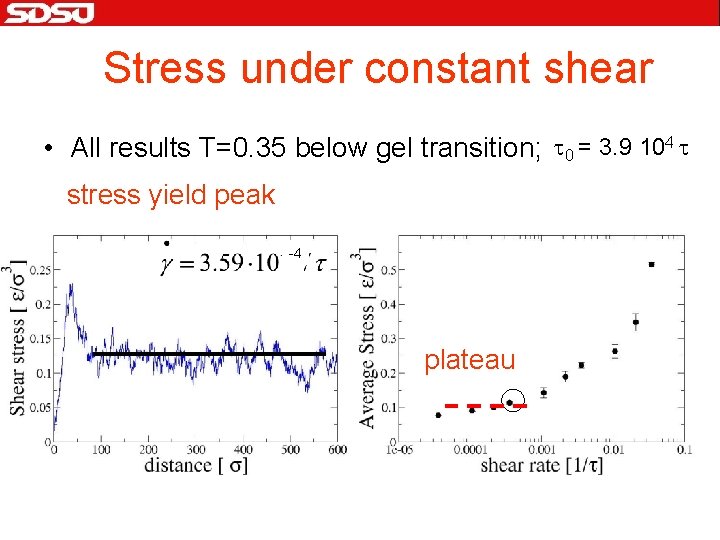
Stress under constant shear • All results T=0. 35 below gel transition; t 0 = 3. 9 104 t stress yield peak -4 plateau

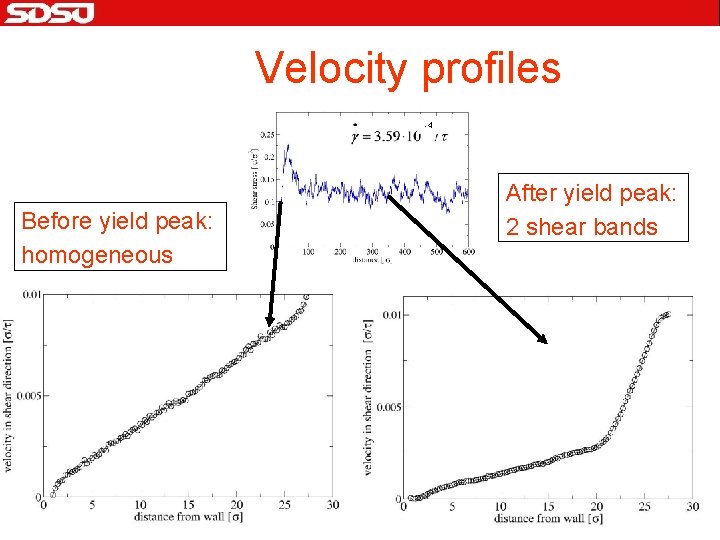
Velocity profiles -4 Before yield peak: homogeneous After yield peak: 2 shear bands

Microscopic differences

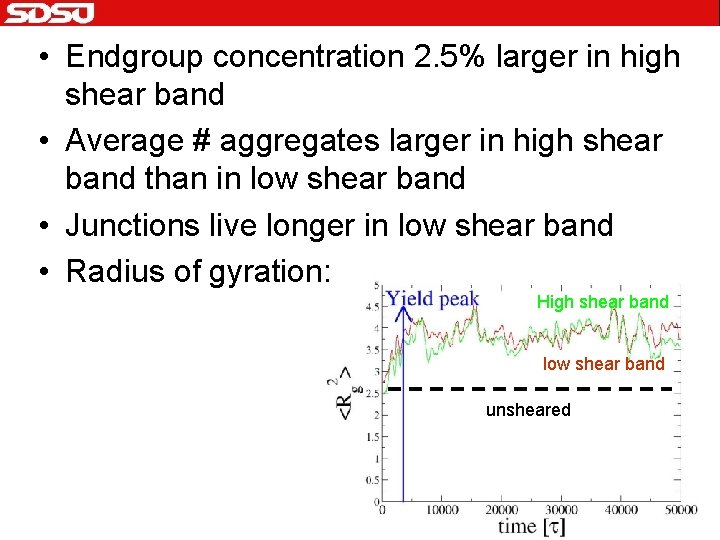
• Endgroup concentration 2. 5% larger in high shear band • Average # aggregates larger in high shear band than in low shear band • Junctions live longer in low shear band • Radius of gyration: High shear band low shear band unsheared

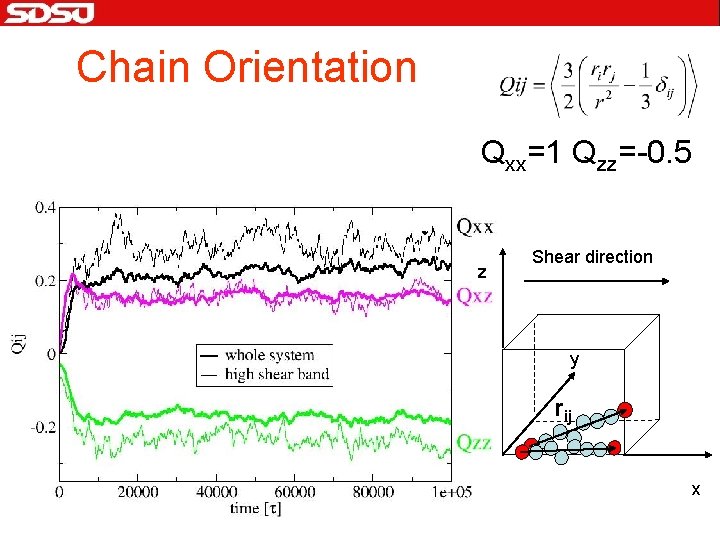
Chain Orientation Qxx=1 Qzz=-0. 5 z Shear direction y rij x

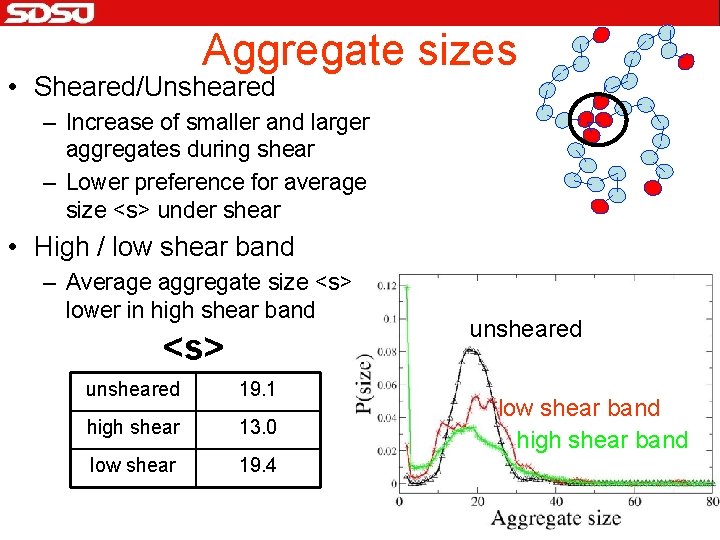
Aggregate sizes • Sheared/Unsheared – Increase of smaller and larger aggregates during shear – Lower preference for average size <s> under shear • High / low shear band – Average aggregate size <s> lower in high shear band <s> unsheared 19. 1 high shear 13. 0 low shear 19. 4 unsheared low shear band high shear band

Topological differences

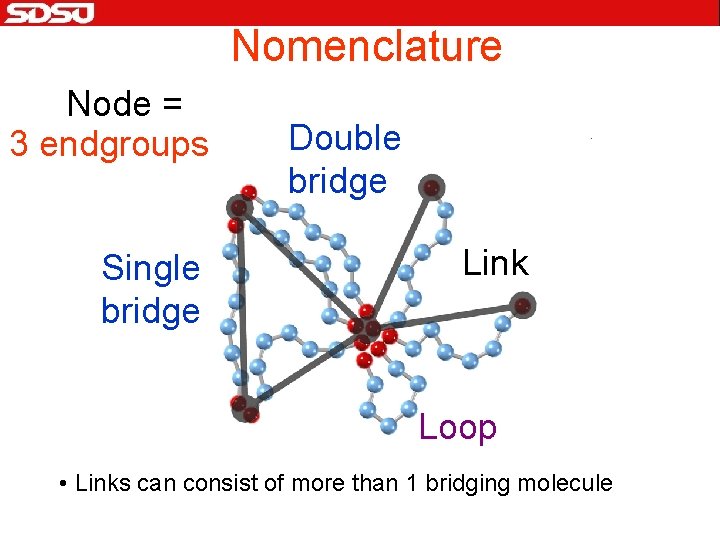
Nomenclature Node = 3 endgroups Single bridge Double bridge Link Loop • Links can consist of more than 1 bridging molecule

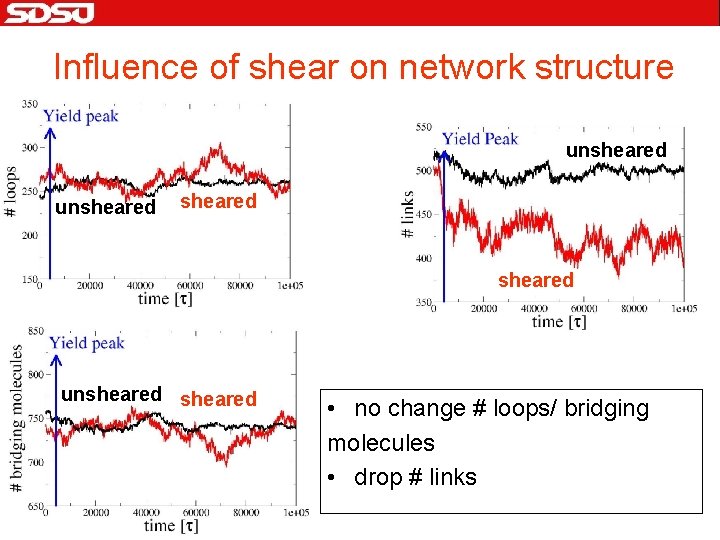
Influence of shear on network structure unsheared unsheared • no change # loops/ bridging molecules • drop # links

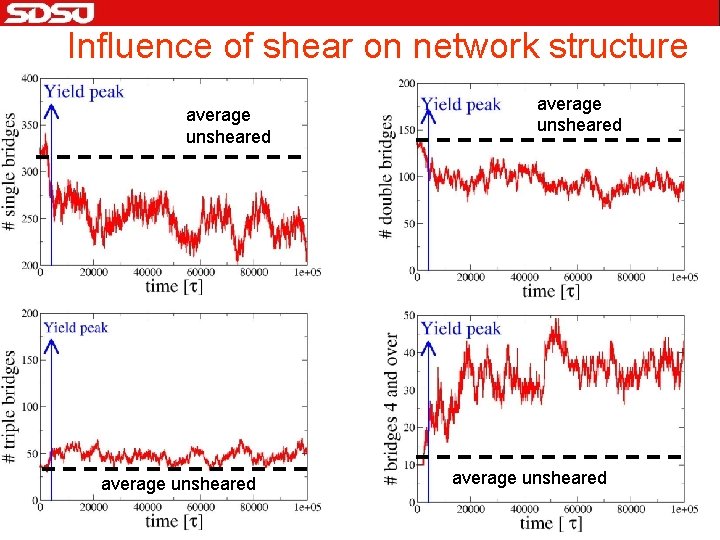
Influence of shear on network structure average unsheared

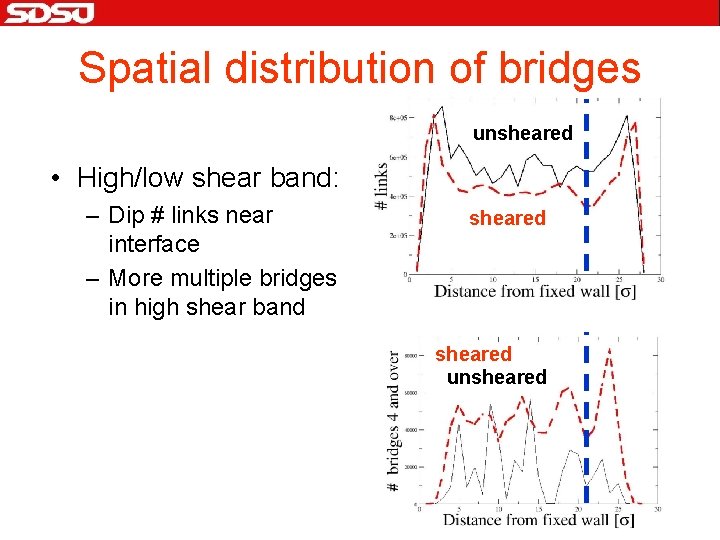
Spatial distribution of bridges unsheared • High/low shear band: – Dip # links near interface – More multiple bridges in high shear band sheared unsheared

Conclusions • MD / MC simulation associating polymers • Shear banding observed in simulations • Study of differences – Sheared vs Unsheared • • Chains orient and Rg increases No change in # loops / # bridging molecules Number of links decreases Formation of links with high # bridging molecules – High vs Low shear band • • More aggregates in high shear band Larger endgroup concentration in high shear band Smaller aggregate size in high shear band More links with high # bridging molecules Poster 49 on Wednesday

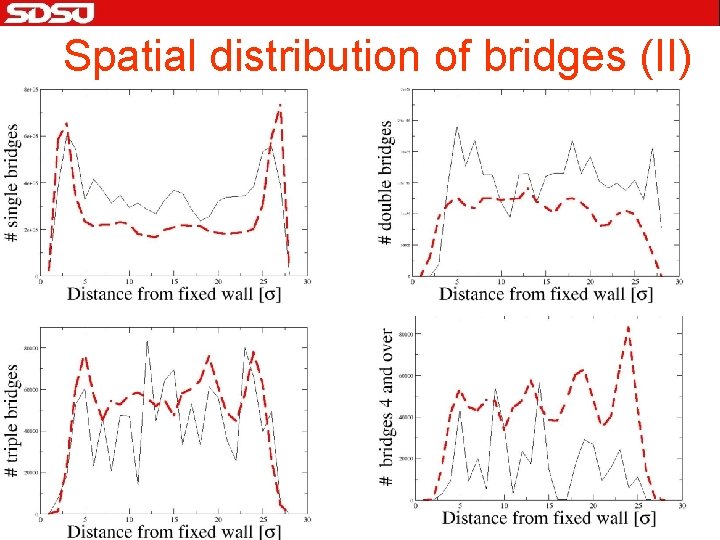
Spatial distribution of bridges (II)

Bead-spring model [K. Kremer and G. S. Krest. J. Chem. Phys 1990] Attraction beads in chain U [e] Repulsion all beads Distance [s] • Temperature control through coupling with heat bath 1 s

[A. Baljon et al. , J. Chem. Phys. , 044907 2007] Associating polymer • Junctions between end groups : FENE + Association energy U [e] U bo nd • Dynamics … Unobond Distance [s]

Dynamics of associating polymer (I) D U [e] • Monte Carlo: attempt to form junction P=1 form P<1 possible form Uassoc Distance [s]

Dynamics of associating polymer (II) -D U [e] • Monte Carlo: attempt to break junction P<1 possible break P=1 break Uassoc Distance [s]

Velocity profile over time • Fluctuations of interface fixed wall velocity [s/t] distance from wall [s] moving wall time [t]

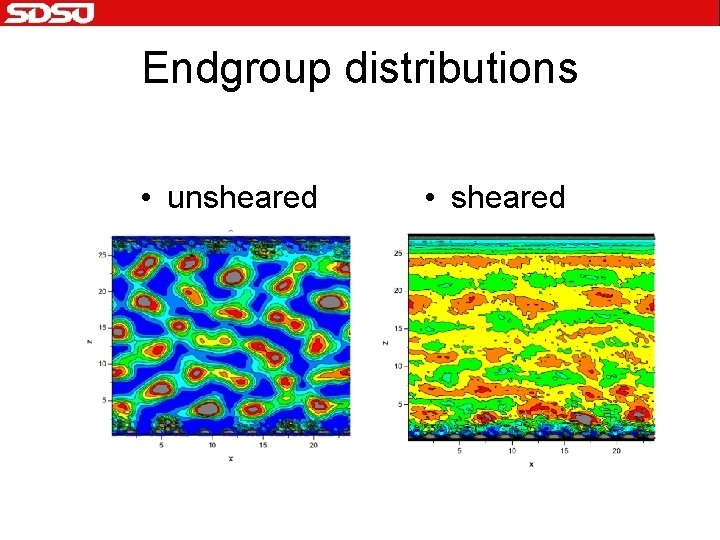
Endgroup distributions • unsheared • sheared