A Comprehensive Study on RAID 6 Codes Horizontal

A Comprehensive Study on RAID 6 Codes: Horizontal vs. Vertical Chao Jin*, Dan Feng*, Hong Jiang†, Lei Tian*† *Huazhong University of Science and Technology †University of Nebraska-Lincoln

Outline • Background • Code-Length Extending Algorithm for Vertical RAID 6 Codes • Performance Analysis and Comparison • Conclusion

Background • RAID 6 Codes RDP - Horizontal Code – Can tolerate two concurrent disk failures (column erasures) • Horizontal RAID 6 Codes – Parity blocks held in dedicated parity columns – Data blocks held in data columns • Vertical RAID 6 Codes – No dedicated parity column – Data columns hold both data and parity blocks P-Code - Vertical Code

Background • RAID 6 Code-Length Restrictions – Lengths (number of columns in the code structure) can not be an arbitrary number – Usually related to a prime number – RDP: prime+1; P-Code: prime-1, prime; … • RAID 6 Code-Length Extensions – Horizontal Codes: easy to extend; just by removing data columns directly – Vertical codes: harder; can not be extended like horizontal codes

Code-Length Extensions for Horizontal Codes Standard RDP Code with 6 columns Extended RDP Code with 5 columns Assume the column contain zeros, remove it from the code structure • • D 1 D 2 (1, 5) (1, 6) D 3 P Q (1) (5) (2, 5) (6) (3, 5) (3, 6) (7) (4, 5) (4, 6) (4, 7) (8) (1, 7) (1, 8) (2, 6) (2, 7) (2, 8) (3, 7) (3, 8) (4) D 4 (3) (2) Code-Length Extension: shortening from a standard code Removing some columns directly from the standard code Result in extended codes with shorter code lengths Removed columns assumed to contain only zeros, thus do not affect the fault-tolerating ability of the extended codes

Code-Length Extensions for Vertical Codes • Vertical codes can not be shortened directly like horizontal codes • Each column contain not only data blocks but also parity blocks • Removing a parity block may leave the parity stripe in an inconsistent state • Tow extending algorithms for vertical codes are proposed D 1 D 2 D 3 D 4 D 5 D 6 (1) (2, 6) (3, 5) (2) (3, 6) (4, 5) (3) (1, 2) (4, 6) (4) (1, 3) (5, 6) (5) (1, 4) (2, 3) (6) (1, 5) (2, 4) Parity stripe P(6) loses the failure recovery ability

Code-Length Extensions for Vertical Codes • First extending algorithm – Select a new parity block for the parity stripe – The parity block is originally a data block of the parity stripe – The parity stripe remain consistent! D 1 D 2 D 3 D 4 D 5 D 6 (1) (2, 6) (3, 5) (2) (3, 6) (4, 5) (3) (1, 2) (4, 6) (4) (1, 3) (5, 6) (5) (1, 4) (2, 3) (6) (1, 5) (2, 4) (5, 6) = (3, 6) (4, 6) (2, 6)

Code-Length Extensions for Vertical Codes • Second extending algorithm – Remove the entire parity stripe from the code structure – Additional data blocks may be removed to keep an equal number of blocks per column – Removed blocks may be assumed to be zero blocks D 1 D 2 D 3 D 4 D 5 D 6 (1) (3, 5) (2, 6) (2) (4, 5) (3, 6) (3) (1, 2) (4, 6) (4) (1, 3) (5, 6) (5) (1, 4) (2, 3) (6) (1, 5) (2, 4)

RAID 6 Code Performance Metrics • Space Efficiency – Ratio between data volume and whole volume (data and parity volume). [Optimal (highest, MDS Codes): (n-2)/n] – Related to the redundant rate of the RAID 6 systems • Update Complexity – Average number of parity blocks need to be updated upon each data block update. [Optimal (lowest): 2] – Impact write overhead of the RAID 6 systems • Computational Complexity – Average number of XOR per data block during encoding/decoding. [Optimal (lowest) for MDS Codes: 22/(n-2) , (n-3)] – Impact CPU overhead of the RAID 6 systems

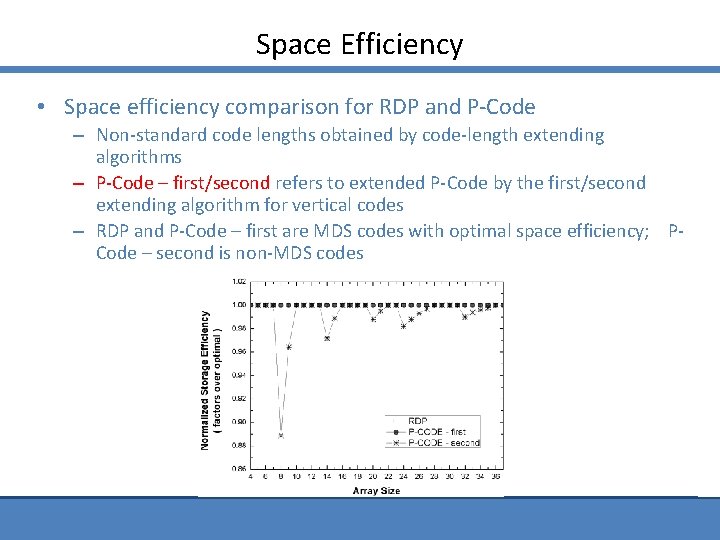
Space Efficiency • Space efficiency comparison for RDP and P-Code – Non-standard code lengths obtained by code-length extending algorithms – P-Code – first/second refers to extended P-Code by the first/second extending algorithm for vertical codes – RDP and P-Code – first are MDS codes with optimal space efficiency; PCode – second is non-MDS codes

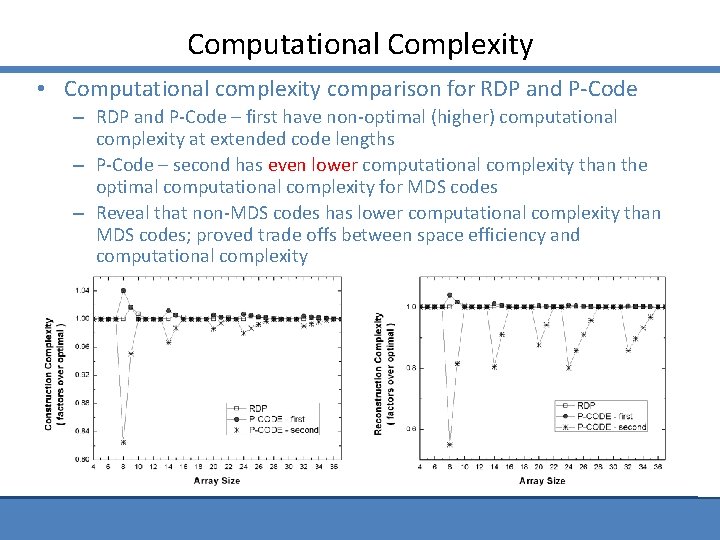
Computational Complexity • Computational complexity comparison for RDP and P-Code – first have non-optimal (higher) computational complexity at extended code lengths – P-Code – second has even lower computational complexity than the optimal computational complexity for MDS codes – Reveal that non-MDS codes has lower computational complexity than MDS codes; proved trade offs between space efficiency and computational complexity

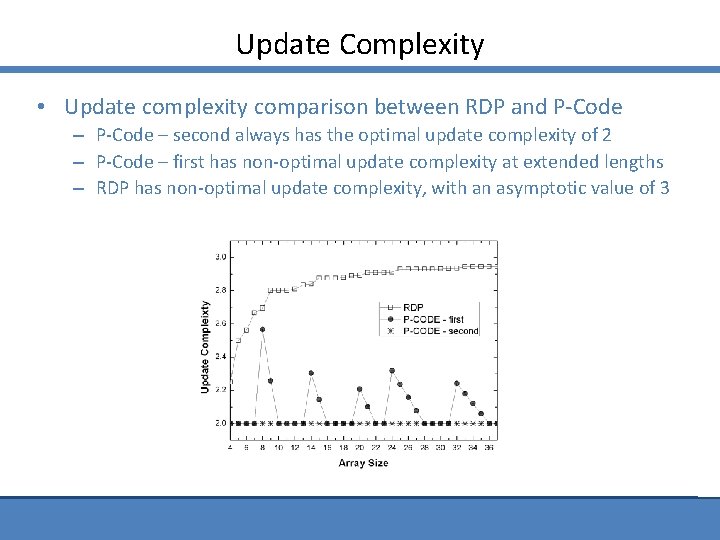
Update Complexity • Update complexity comparison between RDP and P-Code – second always has the optimal update complexity of 2 – P-Code – first has non-optimal update complexity at extended lengths – RDP has non-optimal update complexity, with an asymptotic value of 3

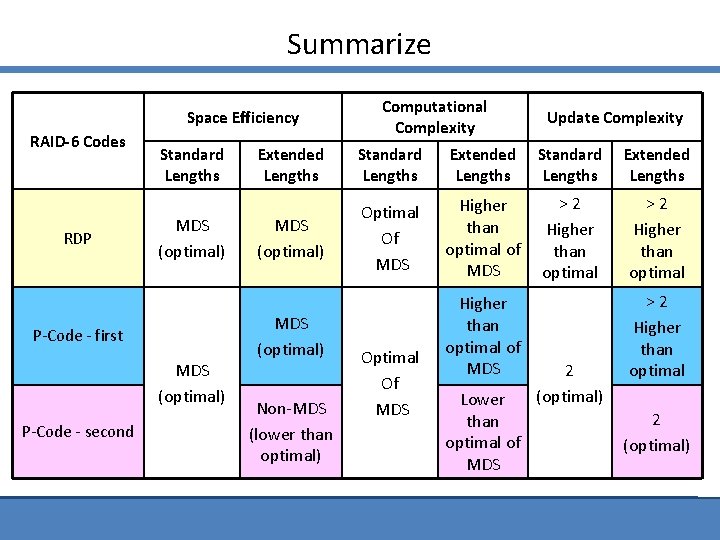
Summarize Space Efficiency RAID-6 Codes RDP Standard Lengths MDS (optimal) P-Code - first MDS (optimal) P-Code - second Computational Complexity Update Complexity Extended Lengths Standard Lengths Extended Lengths MDS (optimal) Optimal Of MDS Higher than optimal of MDS >2 Higher than optimal MDS (optimal) Non-MDS (lower than optimal) Optimal Of MDS Higher than optimal of MDS Lower than optimal of MDS 2 (optimal) >2 Higher than optimal 2 (optimal)

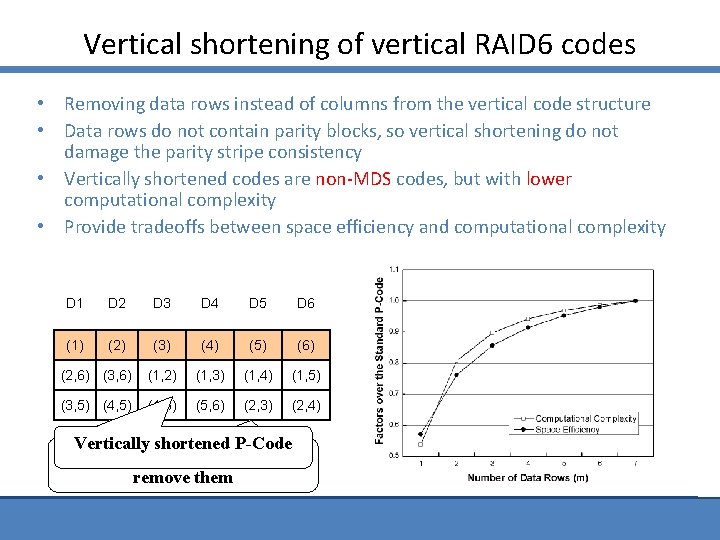
Vertical shortening of vertical RAID 6 codes • Removing data rows instead of columns from the vertical code structure • Data rows do not contain parity blocks, so vertical shortening do not damage the parity stripe consistency • Vertically shortened codes are non-MDS codes, but with lower computational complexity • Provide tradeoffs between space efficiency and computational complexity D 1 D 2 D 3 D 4 D 5 D 6 (1) (2) (3) (4) (5) (6) (2, 6) (3, 6) (1, 2) (1, 3) (1, 4) (1, 5) (3, 5) (4, 6) (5, 6) (2, 3) (2, 4) Vertically shortened P-Code Assume they are zero blocks and remove them

Conclusions • Horizontal codes are easy to be extended to eliminate the code -length restrictions, but vertical codes are not easy to be extended. We proposed two extending algorithms for vertical codes. The first one selects a new parity block for the parity stripe; the second one removes the entire parity stripe from the code structure. • We compared the performance of horizontal codes and vertical codes at consecutive code lengths. We also studied the impact of the code-length extending algorithms on the performance of the RAID 6 codes. • We proposed the vertical shortening algorithm for vertical codes. The algorithm can provide the tradeoff between space efficiency and computational complexity for vertical codes.

Thanks! Email: chjinhust@gmail. com