A Comparison of Simulated Annealing and Genetic Algorithm

A Comparison of Simulated Annealing and Genetic Algorithm Approaches for Cultivation Model Identification Olympia Roeva Institute of Biophysics and Biomedical Engineering Bulgarian Academy of Sciences E-mail: olympia@clbme. bas. bg

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion competing paradigms in the field of modern heuristics Genetic Algorithm Simulated Annealing Algorithm quite close relatives and much of their difference is superficial population size → one population new solutions by → a new solution by modifying only combining two different solutions one solution with a local move (crossover and mutation) (only mutation) In this work, both GA and SA are applied and compared for a parameter identification of non -linear mathematical model of E. coli MC 4110 fed-batch cultivation process.

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion A pseudo code of a GA is presented as: 1. Set generation number to zero (t = 0) 2. Initialise usually random population of individuals (P(0)) 3. Evaluate fitness of all initial individuals of population 4. Begin major generation loop in k: 4. 1. Test for termination criterion 4. 2. Increase the generation number 4. 3. Select a sub-population for offspring reproduction (select P(i) from P(i – 1)) 4. 4. Recombine the genes of selected parents (recombine P(i)) 4. 5. Perturb the mated population stochastically (mutate P(i)) 4. 6. Evaluate the new fitness (evaluate P(i)) 5. End major generation loop

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion Basic GA operators and parameters Operator Type Parameter Value encoding binary ggap 0. 97 fitness function linear ranking xovr 0. 70 mutr 0. 01 nind 100 maxgen 200 selection function roulette wheel selection crossover function double point mutation function bit inversion reinsertion fitness-based

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion A pseudo code of SA could be presented as: 1. Find initial solution (by generating it randomly) 2. Set initial value for the control parameter T = T 0 3. Set a value for r, the rate of cooling parameter j=0 Generate (at random) a new solution S’ Calculate the difference in cost: = cost(S’) – cost(S) Examine the new solution and decide: accept or reject If accepted, it becomes the current solution; otherwise, keep the old one; j = j+1 Reduce the temperature and generate a new solution 4. Until some stopping criterion applies

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion Boltzman distribution with the probability of acceptance: Temperature update: T = T 0 0. 95 r Annealing parameters:

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion Parameter identification of E. coli MC 4110 fed-batch cultivation model Real experimental data of the E. coli MC 4110 fed-batch cultivation are used.

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion A two stage parameter identification procedure is used Objective function

1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion

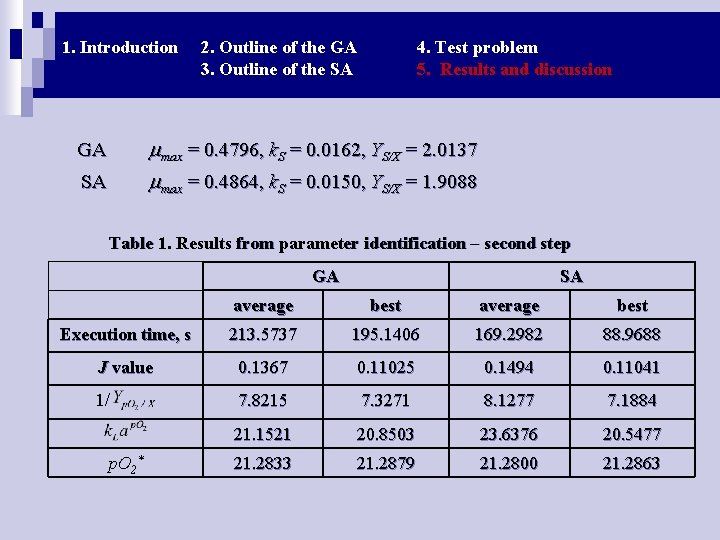
1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion max = 0. 4796, k. S = 0. 0162, YS/X = 2. 0137 max = 0. 4864, k. S = 0. 0150, YS/X = 1. 9088 GA SA Table 1. Results from parameter identification – second step GA SA average best Execution time, s 213. 5737 195. 1406 169. 2982 88. 9688 J value 0. 1367 0. 11025 0. 1494 0. 11041 1/ 7. 8215 7. 3271 8. 1277 7. 1884 21. 1521 20. 8503 23. 6376 20. 5477 21. 2833 21. 2879 21. 2800 21. 2863 p. O 2*

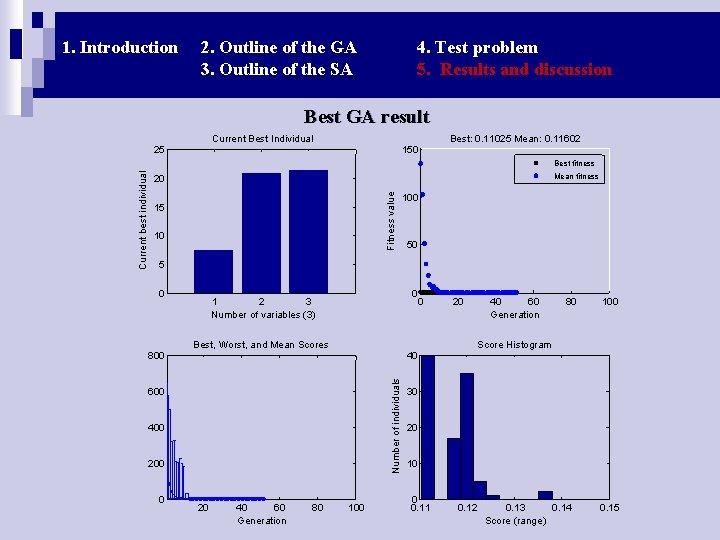
1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion Best GA result Current Best Individual Best: 0. 11025 Mean: 0. 11602 25 150 Mean fitness Fitness value 20 15 10 100 50 5 0 0 1 2 3 Number of variables (3) 0 20 Best, Worst, and Mean Scores 80 100 40 600 400 200 0 40 60 Generation Score Histogram 800 Number of individuals Current best individual Best fitness 20 40 60 Generation 80 100 30 20 10 0 0. 11 0. 12 0. 13 0. 14 Score (range) 0. 15

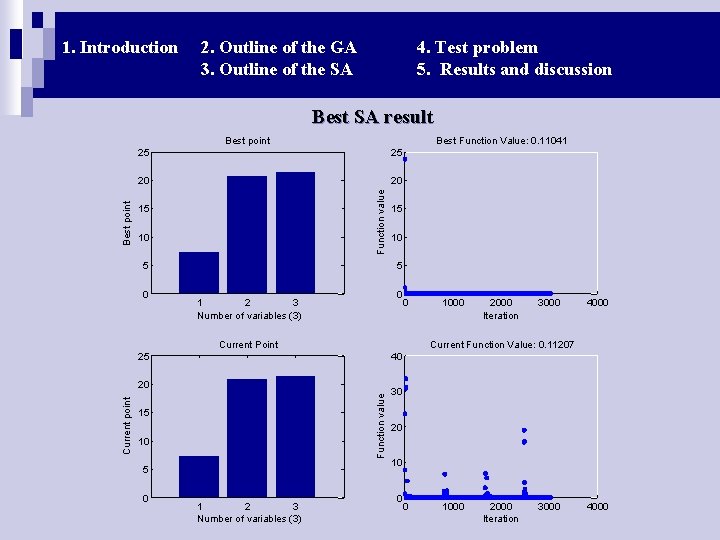
1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion Best SA result Best Function Value: 0. 11041 25 20 20 Function value Best point 25 15 10 5 0 25 0 1 2 3 Number of variables (3) Current Point 15 10 5 1 2 3 Number of variables (3) 0 1000 2000 Iteration 3000 4000 Current Function Value: 0. 11207 40 Function value Current point 10 5 20 0 15 30 20 10 0 0 1000 2000 Iteration 3000 4000

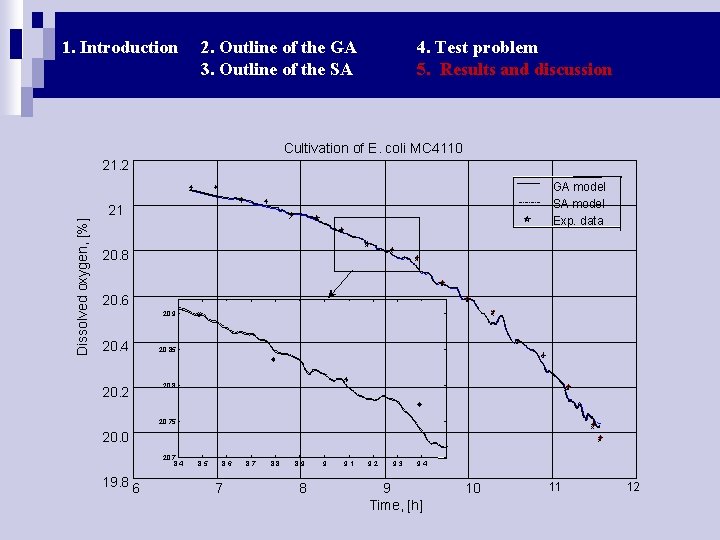
1. Introduction 2. Outline of the GA 3. Outline of the SA 4. Test problem 5. Results and discussion Cultivation of E. coli MC 4110 21. 2 GA model SA model Exp. data Dissolved oxygen, [%] 21 20. 8 20. 6 20. 9 20. 4 20. 2 20. 85 20. 8 20. 75 20. 0 20. 7 8. 4 19. 8 6 8. 5 8. 6 7 8. 8 8. 9 8 9 9. 1 9. 2 9. 3 9. 4 9 Time, [h] 10 11 12