A Comparative Study on Variable Selection for Nonlinear

A Comparative Study on Variable Selection for Nonlinear Classifiers C. 1 Lu , 1 Gestel , 1 Suykens , T. Van J. A. K. S. Van I. Vergote 2, D. Timmerman 2 1 Department 1 Huffel , of Electrical Engineering, Katholieke Universiteit Leuven, Belgium, 2 Department of Obstetrics and Gynecology, University Hospitals Leuven, Belgium Email address: chuan. lu@esat. kuleuven. ac. be

1. Introduction Ø Variable selection refers to the problem of selecting input variables that are relevant for a given task. In pattern recognition, variable selection can have an impact on the economics of data acquisition and on the accuracy and complexity of the classifiers. Ø This study aims at input variable selection for nonlinear blackbox classifiers, particularly multi -layer perceptrons (MLP) and least squares support vector machines (LS-SVMs). 2. Feature extraction Pattern recognition: feature extraction -> classification Variable measure Variable Selection Feature Extraction • • Feature selection or variable selection • Variable (feature) measure • Heuristic search: forward, backward, stepwise, hill-climbing, branch and bound… Feature transformation e. g. PCA, not desirable for maintaining data, difficulty in interpretation, and not immune from distortion under transformation • • Filter approach: filter out irrelevant attributes before induction occurs Wrapper approaches : focus on finding attributes that are useful for performance for a specific type of model, rather than necessarily finding the relevant ones. • Correlation • Mutual information (MI) • Evidence (or Bayes factor) in Bayesian framework • Classification performance • Sensitivity analysis: change in the objective function J by removing variable i: DJ(i) • Statistical partial F test (Chisquare value)

3. Considered nonlinear classifiers: MLPs and LS-SVMs MLP Classifiers LS-SVM Classifier Bayesian Evidence Framework Inferences are divided into distinct levels. solved in dual space Note: by integrating the MLP(Mackay 1992) or LS-SVM (Van. Gestel, Suykens 2002) with the Bayesian evidence framework, the tuning of hyperparameters and computation of posterior class probabilities can be done in a unified way. Variable selection can also be done based on the model evidence. Model evidence

4. Considered variable selection methods Method Variable measure Mutual information Mutual feature selection information under uniform I(X; Y) information distrib. (MIFS-U) [8] Predefined (Dis) advantages parameters Greedy search: begin from Density function Linear/Nolinear, easy to no variables, repeat estimation (parametric compute; computational selecting the feature until or nonparametric), problems increase with k, for predifined k variables are here the simple very high dimensional data. selected discretization method Information lost due to is used. discretization. Bayesian LS-SVM Model evidence Greedy search, select each Kernel type. (Non)linear. Automatically variable forward P(D|H) time a variable that gives select a certain number of selection (LSSVMBthe highest increase in variables that max the FFS) [1] model evidence, until no evidence. Gaussian more increase. assumption. Computationally expensive for high dimensional data. LS-SVM recursive feature elimination (LSSVM-RFE) [7] Stepwise logistic regression (SLR) For linear kernel, use(wi)2 Search Recursively remove the variable(s) that have the smallest DJ(i). Chi-square Stepwise: recursively add (statistical or remove a variable at partial F-test). each step. Kernel type, regularization and kernel parameters. Suitable for very high dimensional data. Computationally expensive for large sample size, and nonlinear kernels. P-values for determining addition or removal of variables in models. Linear, easy to compute. Troubles in case of multicolinearity.

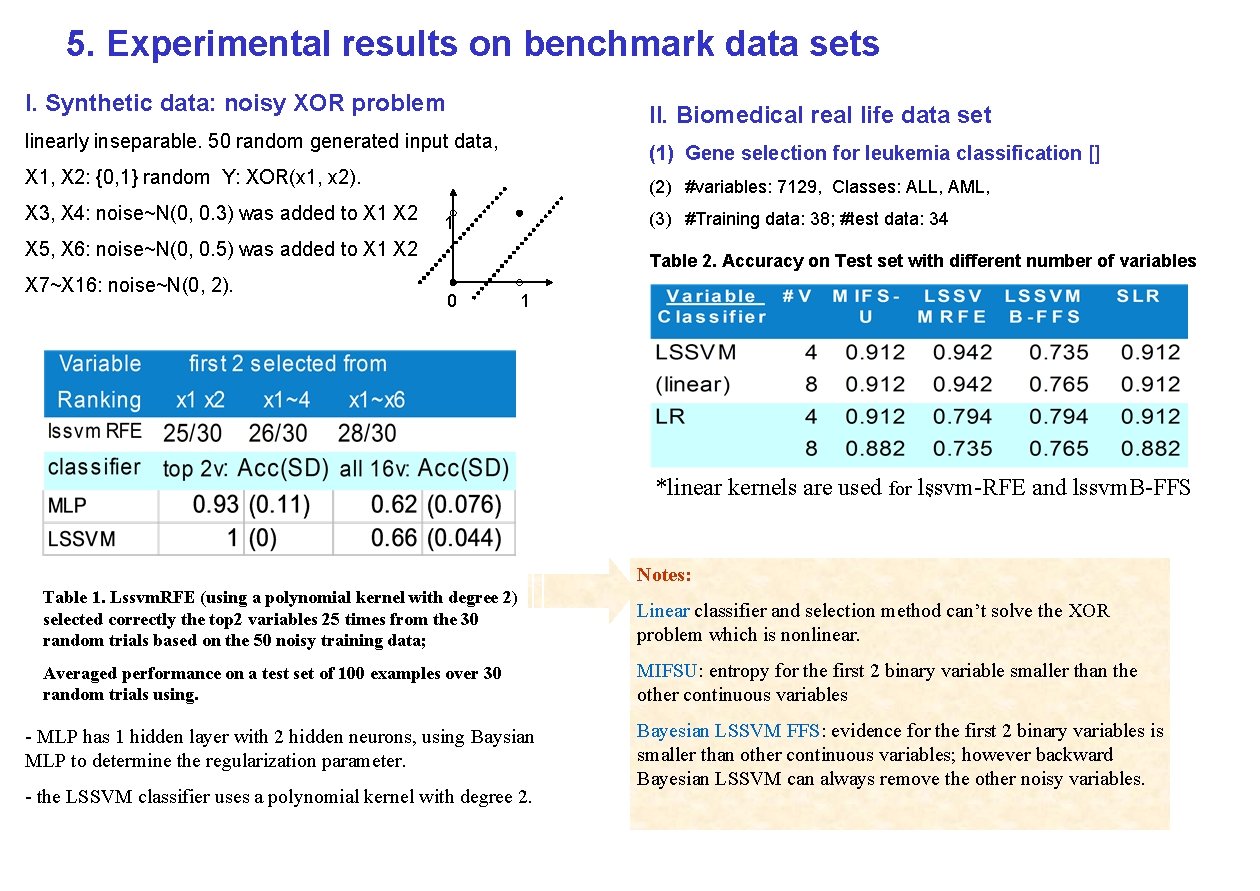
5. Experimental results on benchmark data sets I. Synthetic data: noisy XOR problem II. Biomedical real life data set linearly inseparable. 50 random generated input data, (1) Gene selection for leukemia classification [] X 1, X 2: {0, 1} random Y: XOR(x 1, x 2). X 3, X 4: noise~N(0, 0. 3) was added to X 1 X 2 (2) #variables: 7129, Classes: ALL, AML, (3) #Training data: 38; #test data: 34 1 X 5, X 6: noise~N(0, 0. 5) was added to X 1 X 2 X 7~X 16: noise~N(0, 2). Table 2. Accuracy on Test set with different number of variables 0 1 *linear kernels are used for lssvm-RFE and lssvm. B-FFS. Notes: Table 1. Lssvm. RFE (using a polynomial kernel with degree 2) selected correctly the top 2 variables 25 times from the 30 random trials based on the 50 noisy training data; Linear classifier and selection method can’t solve the XOR problem which is nonlinear. Averaged performance on a test set of 100 examples over 30 random trials using. MIFSU: entropy for the first 2 binary variable smaller than the other continuous variables - MLP has 1 hidden layer with 2 hidden neurons, using Baysian MLP to determine the regularization parameter. - the LSSVM classifier uses a polynomial kernel with degree 2. Bayesian LSSVM FFS: evidence for the first 2 binary variables is smaller than other continuous variables; however backward Bayesian LSSVM can always remove the other noisy variables.

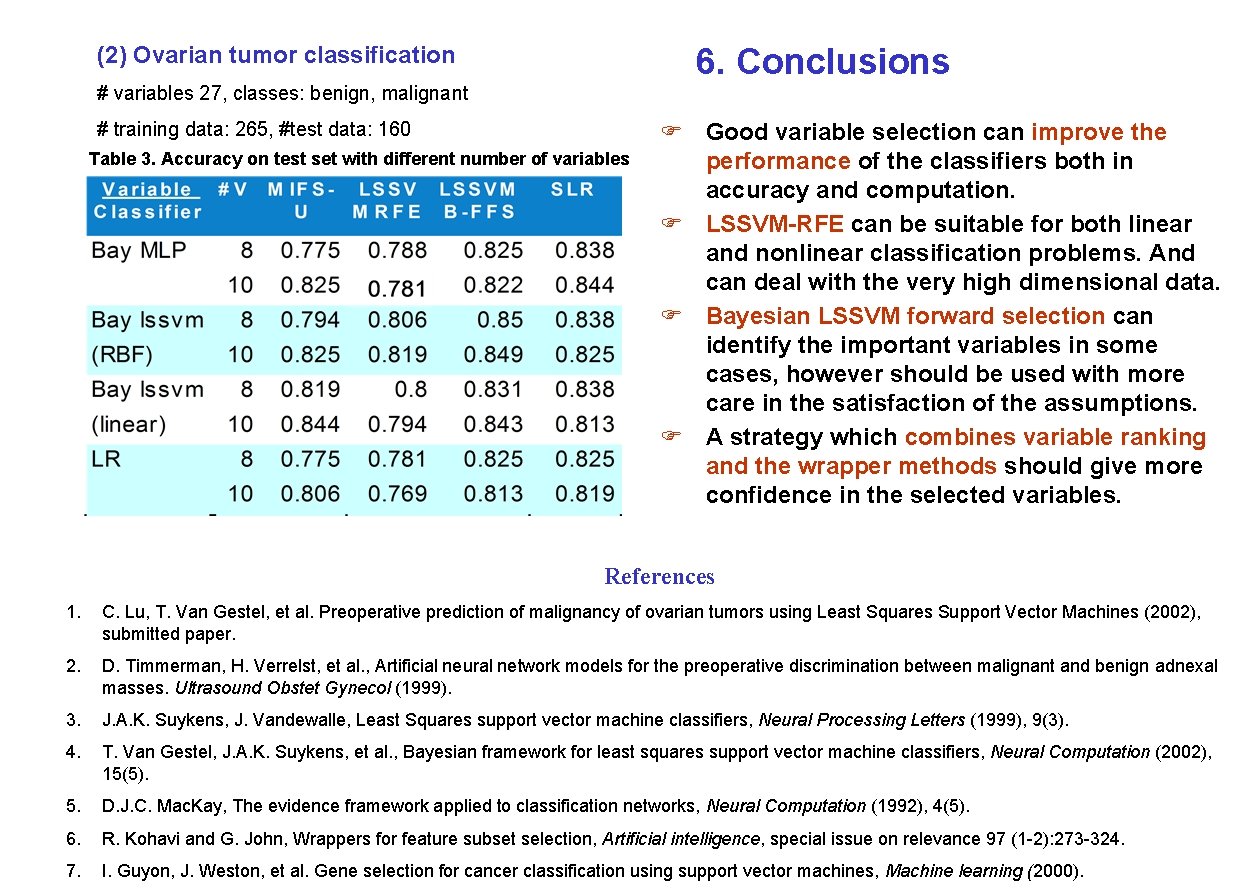
(2) Ovarian tumor classification 6. Conclusions # variables 27, classes: benign, malignant # training data: 265, #test data: 160 Table 3. Accuracy on test set with different number of variables F Good variable selection can improve the performance of the classifiers both in accuracy and computation. F LSSVM-RFE can be suitable for both linear and nonlinear classification problems. And can deal with the very high dimensional data. F Bayesian LSSVM forward selection can identify the important variables in some cases, however should be used with more care in the satisfaction of the assumptions. F A strategy which combines variable ranking and the wrapper methods should give more confidence in the selected variables. References 1. C. Lu, T. Van Gestel, et al. Preoperative prediction of malignancy of ovarian tumors using Least Squares Support Vector Machines (2002), submitted paper. 2. D. Timmerman, H. Verrelst, et al. , Artificial neural network models for the preoperative discrimination between malignant and benign adnexal masses. Ultrasound Obstet Gynecol (1999). 3. J. A. K. Suykens, J. Vandewalle, Least Squares support vector machine classifiers, Neural Processing Letters (1999), 9(3). 4. T. Van Gestel, J. A. K. Suykens, et al. , Bayesian framework for least squares support vector machine classifiers, Neural Computation (2002), 15(5). 5. D. J. C. Mac. Kay, The evidence framework applied to classification networks, Neural Computation (1992), 4(5). 6. R. Kohavi and G. John, Wrappers for feature subset selection, Artificial intelligence, special issue on relevance 97 (1 -2): 273 -324. 7. I. Guyon, J. Weston, et al. Gene selection for cancer classification using support vector machines, Machine learning (2000).