A Common Measure of Identity and Value Disclosure

A Common Measure of Identity and Value Disclosure Risk Krish Muralidhar University of Kentucky krishm@uky. edu Rathin Sarathy Oklahoma State University sarathy@okstate. edu 1

Context n n This study presents developments in the context of numerical data that have been masked and released We assume that the categorical data (if any) have not been masked n This assumption can be relaxed 2

Empirical Assessment of Disclosure Risk n Is there a link between both identity and value disclosure that will allow us to use a “common” measure? 3

Basis for Disclosure n The “strength of the relationship”, in a multivariate sense, between the two datasets (original and masked) accounts for disclosure risk 4

Value Disclosure n n Value disclosure based on “strength of relationship” 2 n Palley & Simonoff(1987) (R measure for individual variables) 2 n Tendick (1992) (R for linear combinations) n Muralidhar & Sarathy(2002) (Canonical Correlation) Implicit assumption – snooper can use linear models to improve their prediction of confidential values (Palley & Simonoff(1987), Fuller(1993), Tendick(1992), Muralidhar & Sarathy(1999, 2001)) 5

Identity Disclosure n Assessment of identity disclosure is often empirical in nature e. g. , Winkler’s software – (Census Bureau) based on a modified Fellegi. Sunter algorithm. n n The number (or proportion) of observations correctly re-identified represents an assessment of identity disclosure risk Theoretical attempts for numerical data: n n n Fuller (1993) (Linear model) Tendick (1992) (Linear model) Fienberg, Makov, Sanil (1997) (Bayesian) 6

Fuller’s Measure n n Given the masked dataset Y, and the original dataset X, and assuming normality, the probability that the jth released record corresponds to any particular record that the intruder may possess is given by Pj = ( kt)-1 kj. The intruder chooses the record j which maximizes kj given by: exp{-0. 5 (X – YH)A-1(X – YH)`}, where A = XX – XY( YY)-1 YX and H = ( YY)-1 YX n Pj may be treated as the identification probability (identity risk) of any particular record and averaging over every record gives a mean identification probability or mean identity disclosure risk for whole masked dataset 7

Fuller’s distance measure n n n Based on best conditional densities While restricted to normal datasets, it relates identity risk to the association between the two datasets (though somewhat indirectly) as indicated by kj which contains XY. Shows the connection between distancebased measures and probability-based measures 8

Our Goal n n n To show that both value disclosure and identity disclosure are determined by the degree of association between the masked and original datasets. This must be true, since both are based on best predictors When the best predictors are linear (e. g. , multivariate normal datasets) canonical correlation capture the association, and both value disclosure and identity disclosure risk must be expressible in terms of canonical correlations Already shown for value disclosure (Muralidhar et al. 1999, and Sarathy et al. 2002). We will show here the relationship between identity disclosure and canonical correlation 9

Canonical Correlation Version of Fuller’s Distance Measure (X – YH)A-1(X – YH)` = (U – V 0. 5) C-1 (U – V 0. 5)` , where U = X( xx)-0. 5 e (the canonical variates for the X variables) V = Y( yy)-0. 5 f (the canonical variates for the Y variables) C = (I – λ) e is eigenvector of ( XX)-0. 5 XY( YY)-1 YX( XX)-0. 5 ( )-1 ( )-0. 5. n f is eigenvector of ( ) YY YX XX XY YY n is diagonal matrix of eigenvalues and is also the vector of squared canonical correlations n 10

Therefore… n n n Identity disclosure risk is a function of the (linear) association between the two datasets (the lambdas, which are the square of the canonical correlations) (U – V 0. 5) (I- )-1 (U – V 0. 5)` relates this association to identity disclosure as well as provide an “operational” way to assess this risk. Compute this distance measure and match each original record to masked record that minimizes the expression. Then the number of re-identified records gives an overall empirical assessment of identity disclosure risk for a masked data release (Empirical results shown later. ) 11

Mean Identification Probability (MIDP) n Tendick computed bounds on identification probabilities for correlated additive noise methods n n His expressions are specific to the method and not for the general case We show a lower bound on MIDP for the general case (regardless of masking technique) that is based on canonical correlations 12

Bound on MIDP n For a data set (size n) with k confidential variables X, masked using any procedure to result in Y, the mean identification probability is given by: 13

Identification Probability (IDP) n For any given observation i in the original data set, the probability that it will be reidentified is given by: where Uij is the canonical variate for Xij 14

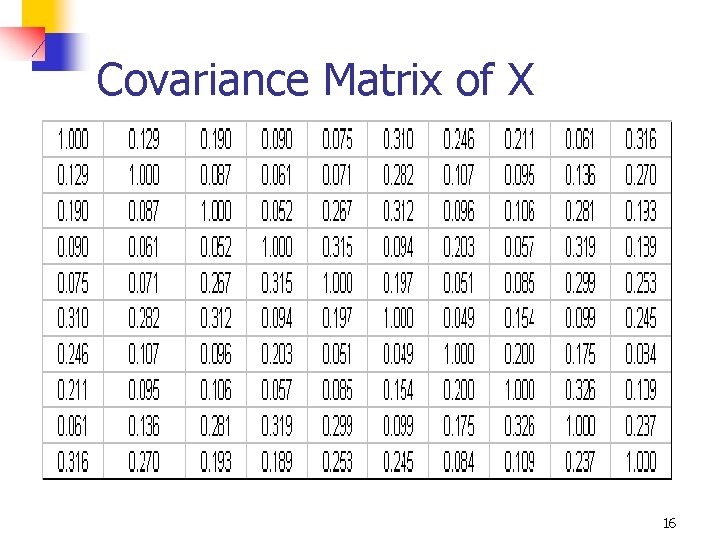
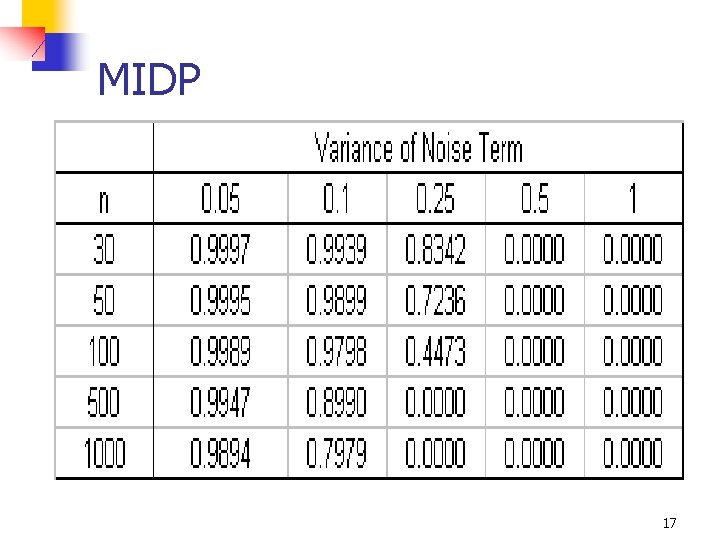
An Example n n n Consider a data set with 10 variables and a specified covariance matrix Assume that the data is to be perturbed using simple noise addition with different levels of variance Compute MIDP for different sample sizes and different noise variances 15

Covariance Matrix of X 16

MIDP 17

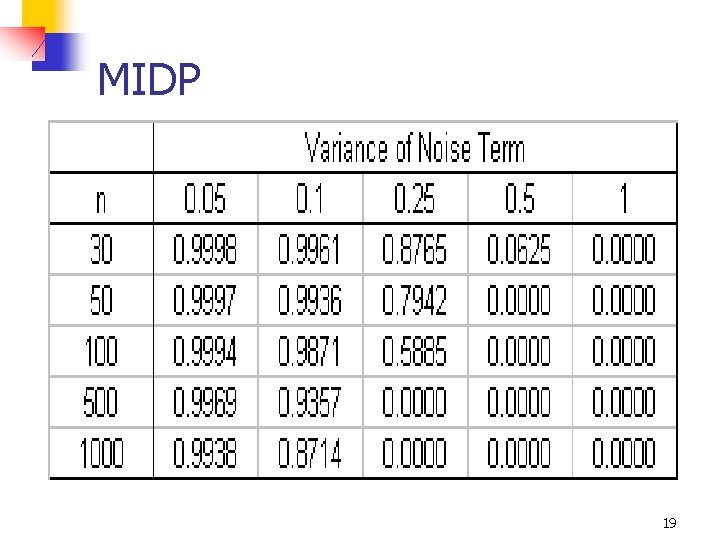
Additive (Correlated) Noise n n Kim (1986) suggested that covariance structure of the noise term should be the same as that of the original confidential variables (dΣXX) where d is a constant representing the “level” of noise In this case, canonical correlation for each (masked, original) variable pair is [1/(1+d)]0. 5 18

MIDP 19

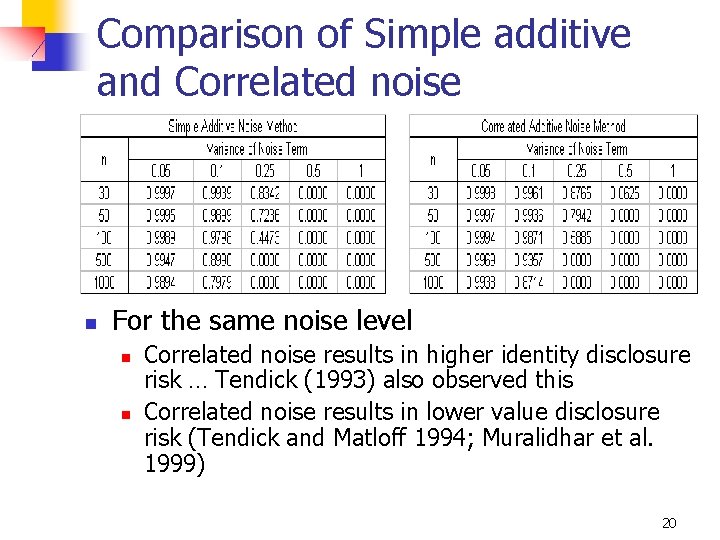
Comparison of Simple additive and Correlated noise n For the same noise level n n Correlated noise results in higher identity disclosure risk … Tendick (1993) also observed this Correlated noise results in lower value disclosure risk (Tendick and Matloff 1994; Muralidhar et al. 1999) 20

Other Procedures n For some other procedures (microaggregation, data swapping, etc. ), it may be necessary to perform the masking and use the data to compute the canonical correlations 21

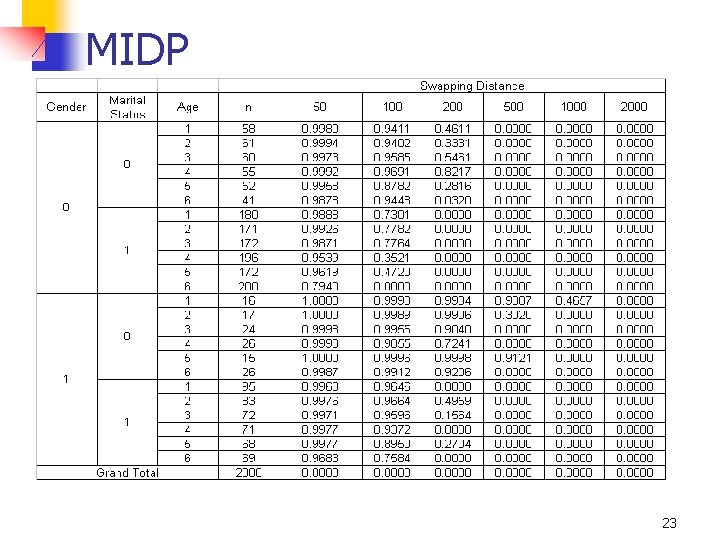
Data sets with Categorical nonconfidential Variables n n MIDP can be computed for subsets as well Example n n n Data set with 2000 observations Six numerical variables Three categorical (non-confidential) variables n n Gender Marital status Age group (1 – 6) Masking procedure is Rank Based Proximity Swap 22

MIDP 23

Using IDP n We can use the IDP bound to implement a record re-identification procedure by choosing masked record with highest IDP value 24

An IDP Example n n n Data set consisting of 25 observations from a MVN(0, 1) Perturbed using independent noise with variance = 0. 45 MIDP = 0. 2375 n n Approximately 6 observations should be reidentified using this criteria Re-identification by chance = 1/n = 0. 04 25

An IDP Example 26

Advantages n n n Possible to compute MIDP with just aggregate information Possible to use IDP as “recordlinkage” tool for assessing disclosure risk characteristics of a masking technique Computationally easier than alternative existing methods 27

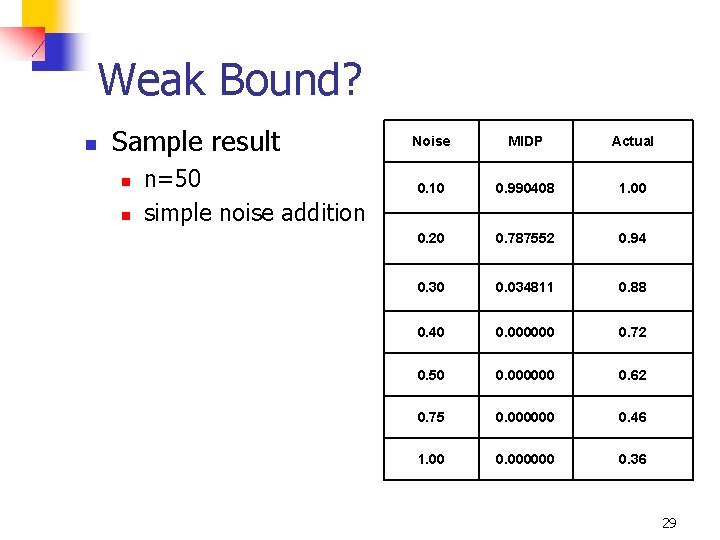
Disadvantages n n Assumes that the data has a multivariate normal distribution For large n, the lower bound is weak. MIDP appears to be overly pessimistic, we are working on finding out why this is so, and possibly modifying the bound. 28

Weak Bound? n Sample result n n n=50 simple noise addition Noise MIDP Actual 0. 10 0. 990408 1. 00 0. 20 0. 787552 0. 94 0. 30 0. 034811 0. 88 0. 40 0. 000000 0. 72 0. 50 0. 000000 0. 62 0. 75 0. 000000 0. 46 1. 00 0. 000000 0. 36 29

Conclusion n n Canonical correlation analysis can be used to assess both identity and value disclosure For normal data, this provides the best measure of both identity and value disclosure 30

Further Research n n n Sensitivity to normality assumption Comparison with Fellegi-Sunter based record linkage procedures Refining the bounds 31

Our Research n You can find the details of our current and prior research at: http: //gatton. uky. edu/faculty/muralidhar 32