A changing electric field generates a magnetic field

A changing electric field generates a magnetic field; conversely a changing magnetic field generates an electric field. Electric fields Magnetic fields • • • Electric fields arise from voltage. Their strength is measured in Volts per metre (V/m) An electric field can be present even when a device is switched off. Field strength decreases with distance from the source. Most building materials shield electric fields to some extent. • • Magnetic fields arise from current flows. Their strength is measured in amperes per meter (A/m). Commonly, EMF investigators use a related measure, flux density (in microtesla (µT) or millitesla (m. T) instead. Magnetic fields exist as soon as a device is switched on and current flows. Field strength decreases with distance from the source. Magnetic fields are not attenuated by most materials.

“Location” in three dimensional space • z Cartesian coordinates are easy – three unit vectors, all orthogonal to one another Az • dz infinitesimal surface area dy – dx · dy – dy · dz – dx · dz • Ay Ax infinitesimal volume element – dx · dy · dz dx x y

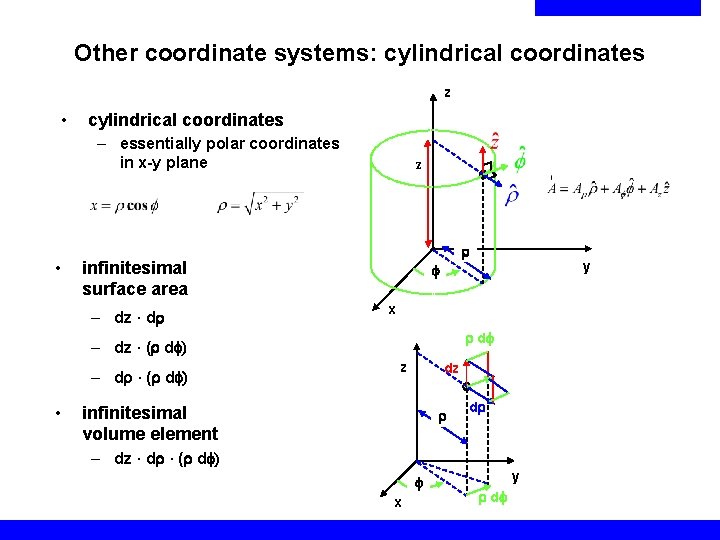
Other coordinate systems: cylindrical coordinates z • cylindrical coordinates – essentially polar coordinates in x-y plane • z r infinitesimal surface area – dz · dr x r d – dz · (r d ) – dr · (r d ) • y z dz infinitesimal volume element r dr – dz · dr · (r d ) x y r d

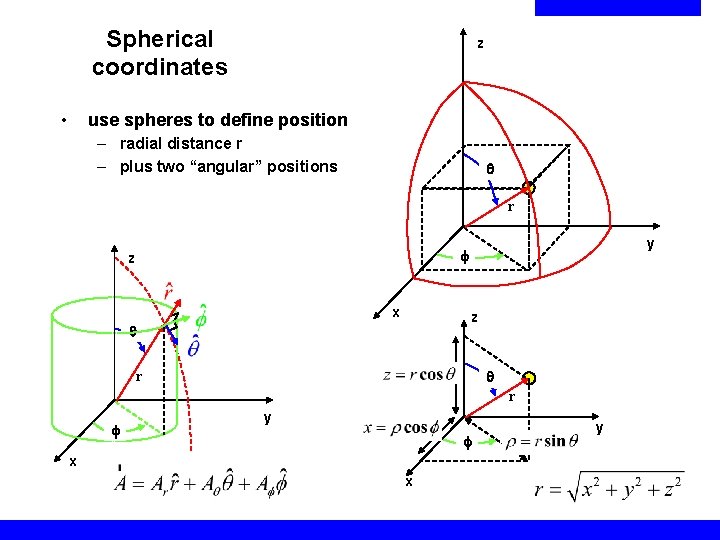
Spherical coordinates • z use spheres to define position – radial distance r – plus two “angular” positions q r y z x z q q r r y x x y

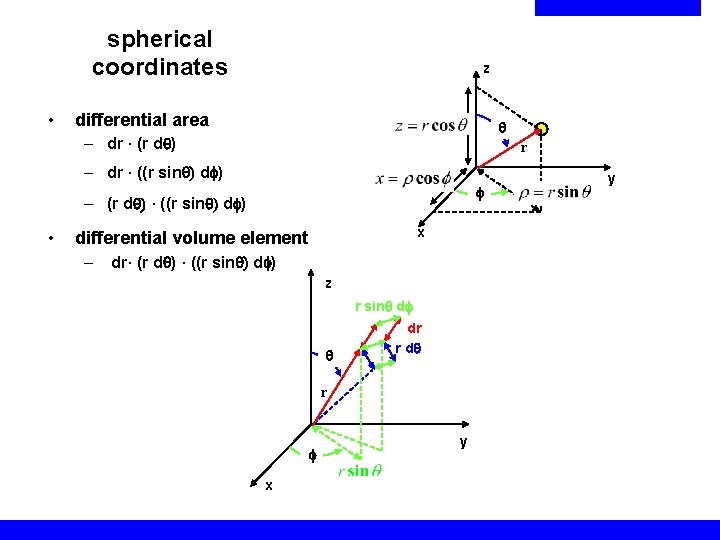
spherical coordinates • z differential area q – dr · (r dq) r – dr · ((r sinq) d ) – (r dq) · ((r sinq) d ) • x differential volume element – dr· (r dq) · ((r sinq) d ) z r sinq d q dr r dq r x y y

“operations” defined in this space • “scalar operations” – result is a simple number, without a “direction” – dot product • “vector operations” – result has both direction and magnitude, i. e. , it is still a vector – vector addition / subtraction – cross product

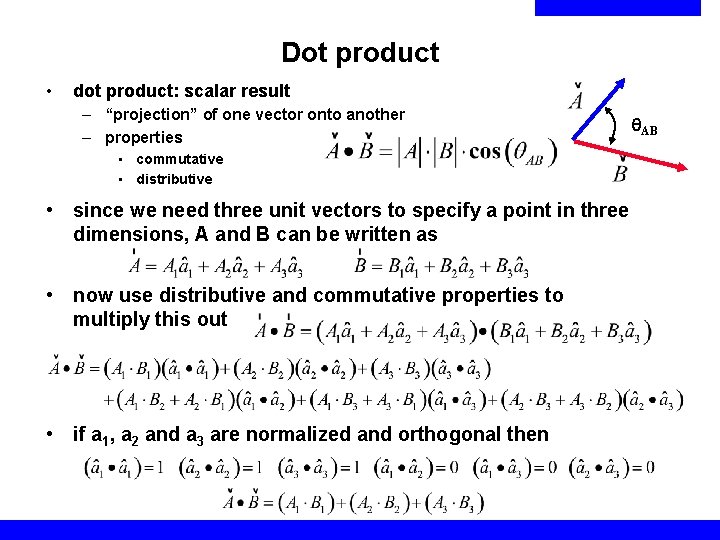
Dot product • dot product: scalar result – “projection” of one vector onto another – properties • commutative • distributive • since we need three unit vectors to specify a point in three dimensions, A and B can be written as • now use distributive and commutative properties to multiply this out • if a 1, a 2 and a 3 are normalized and orthogonal then q. AB

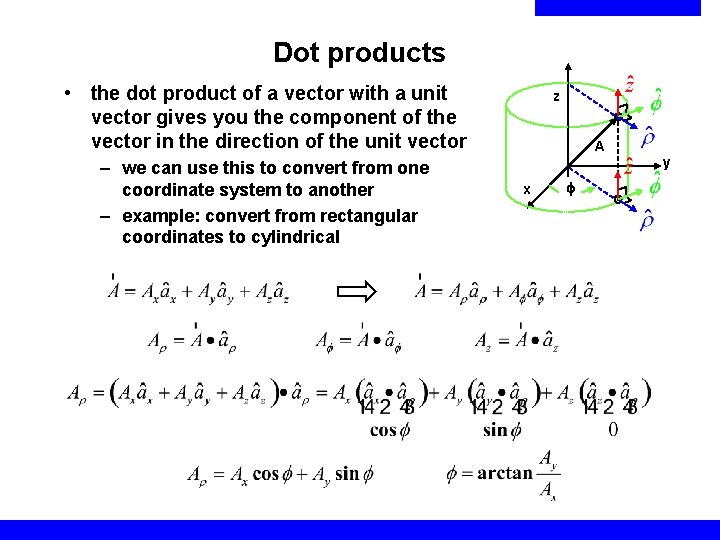
Dot products • the dot product of a vector with a unit vector gives you the component of the vector in the direction of the unit vector – we can use this to convert from one coordinate system to another – example: convert from rectangular coordinates to cylindrical z A y x

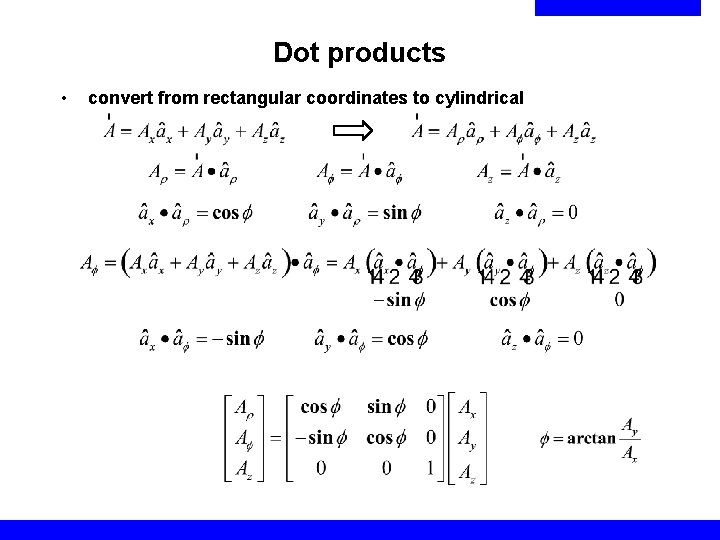
Dot products • convert from rectangular coordinates to cylindrical

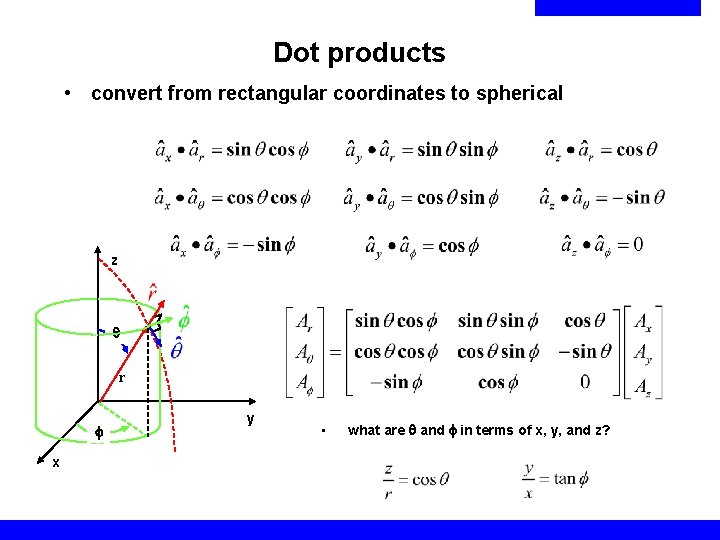
Dot products • convert from rectangular coordinates to spherical z q r x y • what are q and in terms of x, y, and z?

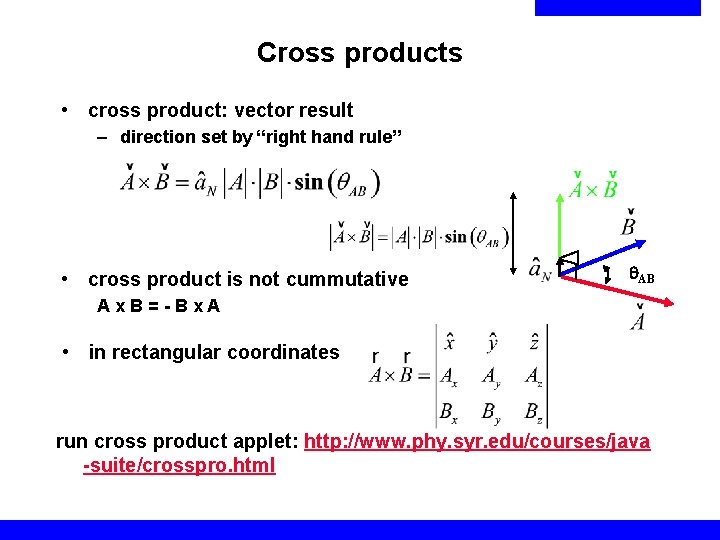
Cross products • cross product: vector result – direction set by “right hand rule” • cross product is not cummutative q. AB Ax. B=-Bx. A • in rectangular coordinates run cross product applet: http: //www. phy. syr. edu/courses/java -suite/crosspro. html