A Categorization of Major Clustering Methods Partitioning approach








































- Slides: 47

A Categorization of Major Clustering Methods • Partitioning approach: • Given a database of n objects or data tuples, a partitioning method constructs k partitions of the data, where each partition represents a cluster and k ≤ n. • The data in the cluster must satisfy following requirements: • 1) Each group must contain at least one object, and • 2) Each object must belong to exactly one group. Ajith G. S: poposir. orgfree. com

A Categorization of Major Clustering Methods • Partitioning approach: • Given k, the number of partitions to construct, a partitioning method creates an initial partitioning. • Then uses an iterative relocation technique Improves the partitions by moving objects between clusters. • Typical methods: k-means, k-medoids, CLARANS Ajith G. S: poposir. orgfree. com

A Categorization of Major Clustering Methods • Hierarchical approach: • Creates a hierarchical decomposition of the given set of data objects. • Classified as being either agglomerative or divisive • Agglomerative approach(bottom-up approach) starts with each object forming a separate group. • It successively merges the objects or groups that are close to one another, until all of the groups are merged into one or until a termination condition holds. Ajith G. S: poposir. orgfree. com

A Categorization of Major Clustering Methods • Hierarchical approach: • Divisive approach (top-down approach) starts with all of the objects in the same cluster. • In each successive iteration, a cluster is split up into smaller clusters, until eventually each object is in one cluster, or until a termination condition holds • Typical methods: Diana, Agnes, BIRCH, ROCK, CHAMELEON Ajith G. S: poposir. orgfree. com

A Categorization of Major Clustering Methods Density-based approach: Discovers clusters with arbitrary shape Based on connectivity and density functions General idea is to continue growing the given cluster as long as the density (number of objects or data points) in the “neighborhood” exceeds some threshold • For each data point within a given cluster, the neighborhood of a given radius has to contain at least a minimum number of points. • Such a method can be used to filter out noise (outliers)and discover clusters of arbitrary shape. • Typical methods: DBSACN, OPTICS, Den. Clue • • Ajith G. S: poposir. orgfree. com

A Categorization of Major Clustering Methods • Grid-based approach: • Grid-based methods quantize the object space into a finite number of cells that form a grid structure • All of the clustering operations are performed on the grid structure • Advantage is the fast processing time. • Typical methods: STING, Wave. Cluster, CLIQUE • Model-based: • A model is hypothesized for each of the clusters and tries to find the best fit of that model to each other • Typical methods: EM, SOM, COBWEB Ajith G. S: poposir. orgfree. com

A Categorization of Major Clustering Methods Partitioning Methods • Given D, a data set of n objects, and k, the number of clusters to form, a partitioning algorithm organizes the objects into k partitions (k ≤ n), where each partition represents a cluster • The clusters are formed so that the objects within a cluster are “similar, ” whereas the objects of different clusters are “dissimilar” in terms of the data set attributes. Ajith G. S: poposir. orgfree. com

Classical Partitioning Methods: k-Means and k-Medoids • Centroid-Based Technique: The k-Means Method • Representative Object-Based Technique: The k. Medoids Method • Partitioning Methods in Large Databases: From k. Medoids to CLARANS Ajith G. S: poposir. orgfree. com

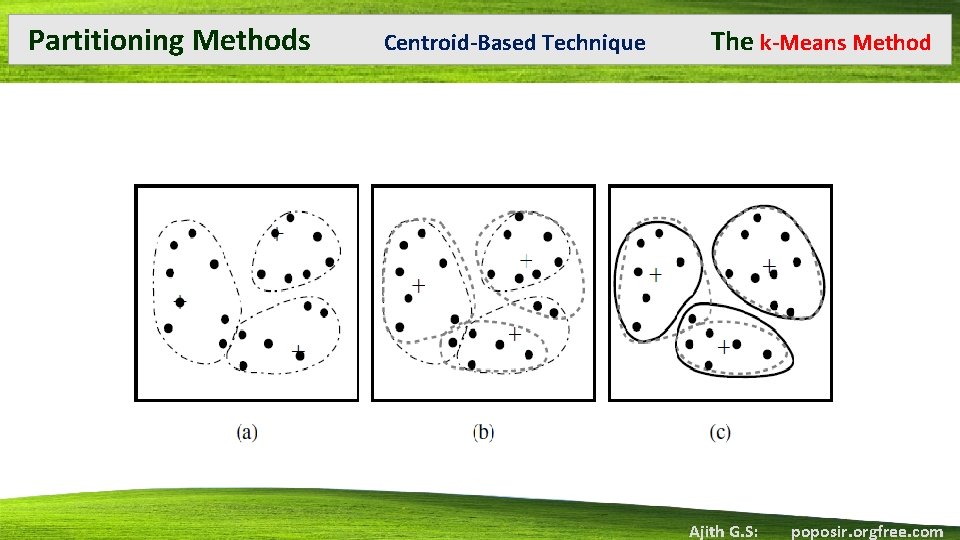
Partitioning Methods • • The k-Means Method Centroid-Based Technique Randomly selects k objects initially represents a cluster mean or center. For each of the remaining objects, an object is assigned to the cluster to which it is the most similar based on the distance between the object and the cluster mean Computes the new mean for each cluster. This process iterates until the criterion function converges Points don’t move or the cluster stabilize E : sum of the square error for all objects in the data set p : point in space representing a given object mi : mean of cluster Ci (both p and mi are multidimensional) Ajith G. S: poposir. orgfree. com

Partitioning Methods Centroid-Based Technique The k-Means Method Ajith G. S: poposir. orgfree. com

Partitioning Methods • • • Centroid-Based Technique The k-Means Method- Algorithm Each cluster’s center is represented by the mean value of the objects in the cluster. Input: k: the number of clusters, D: a data set containing n objects. Output: A set of k clusters. Method: (1) arbitrarily choose k objects from D as the initial cluster centers; (2) repeat (3) reassign each object to the cluster to which the object is the most similar, based on the mean value of the objects in the cluster; (4) update the cluster means, i. e. , calculate the mean value of the objects for each cluster; (5) until no change; Ajith G. S: poposir. orgfree. com

Partitioning Methods Centroid-Based Technique The k-Means Method • Disadvantages • Can be applied only when the mean of a cluster is defined. • The necessity for users to specify k, the number of clusters, in advance • It is not suitable for discovering clusters with nonconvex shapes or clusters of very different size • Sensitive to noise and outlier data points Ajith G. S: poposir. orgfree. com

Partitioning Methods Centroid-Based Technique The k-Means Method • Variants of K-Means • First apply a hierarchical agglomeration algorithm, which determines the number of clusters and finds an initial clustering, and then use iterative relocation to improve the clustering. • k-modes method, which extends the k-means paradigm to cluster categorical data by replacing the means of clusters with modes • The EM (Expectation-Maximization) algorithm extends the k-means paradigm. In EM each object is assigned to each cluster according to a weight representing its probability membership Ajith G. S: poposir. orgfree. com

Partitioning Methods Object-Based The k-Medoids Method • Representative Object-Based Technique: To minimize the sensitivity of k-means to outliers Picks actual objects to represent clusters instead of mean values Each remaining object is clustered with the representative object (Medoid) to which is the most similar The algorithm minimizes the sum of the dissimilarities between each object and its corresponding reference point An absolute-error criterion is used, defined as • • • E : sum of the absolute error for all objects in the data set; p : point in space representing a given object in cluster Cj; oj : representative object of Cj • • • Ajith G. S: poposir. orgfree. com

Partitioning Methods Object-Based The k-Medoids Method • The algorithm iterates until each representative object is actually the medoid, or most centrally located object, of its cluster basis of the k-medoids method • The initial representative objects (or seeds) are chosen arbitrarily. • The iterative process of replacing representative objects by non-representative objects continues as long as the quality of the resulting clustering is improved • Quality is estimated using a cost function that measures the average dissimilarity between an object and the representative object of its cluster Ajith G. S: poposir. orgfree. com

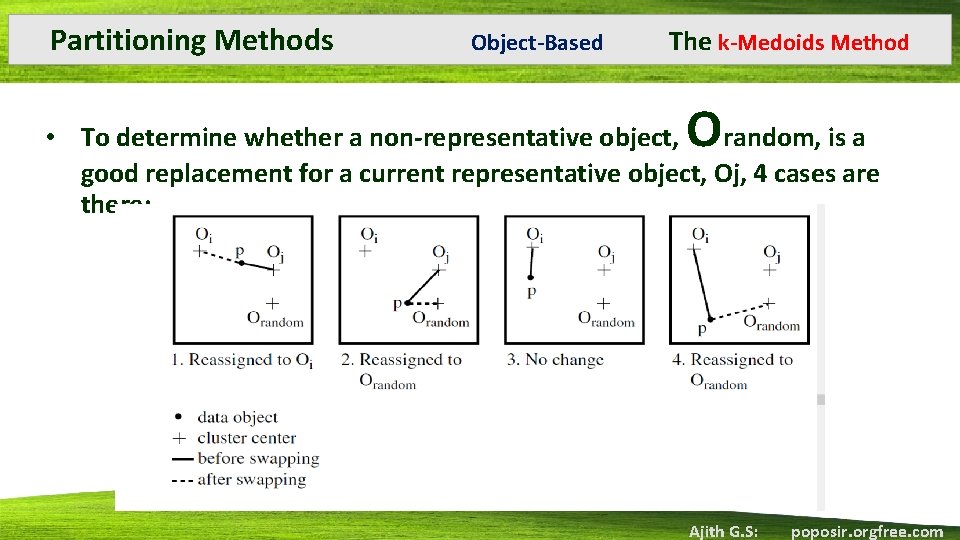
Partitioning Methods Object-Based The k-Medoids Method O • To determine whether a non-representative object, random, is a good replacement for a current representative object, Oj, 4 cases are there: Ajith G. S: poposir. orgfree. com

Partitioning Methods Object-Based The k-Medoids Method • Case 1: p currently belongs to representative object, oj. If oj is replaced by orandom as a representative object and p is closest to one of the other representative objects, oi, i 6= j, then p is reassigned to oi. • Case 2: p currently belongs to representative object, oj. If oj is replaced by orandom as • a representative object and p is closest to orandom, then p is reassigned to orandom. • Case 3: p currently belongs to representative object, oi, i 6= j. If oj is replaced by orandom as a representative object and p is still closest to oi, then the assignment does not change. • Case 4: p currently belongs to representative object, oi, i 6= j. If oj is replaced by orandom as a representative object and p is closest to orandom, then p is reassigned to orandom. Ajith G. S: poposir. orgfree. com

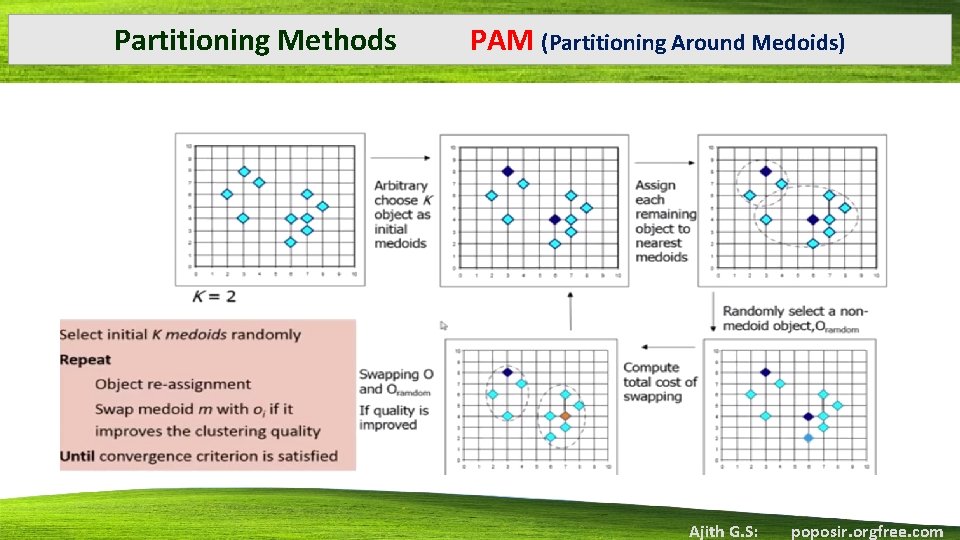
Partitioning Methods PAM (Partitioning Around Medoids) • k-medoids attempts to determine k partitions for n objects • Repeatedly tries to make a better choice of cluster representatives. • All of the possible pairs of objects are analyzed, where one object in each pair is considered representative object and the other is not • An object, Oj, is replaced with the object causing the greatest reduction in error. • The set of best objects for each cluster in one iteration forms the representative objects for the next iteration. • The final set of representative objects are the respective medoids of the clusters. The complexity of each iteration is O(k(n-k)2) Ajith G. S: poposir. orgfree. com

Partitioning Methods • • • PAM (Partitioning Around Medoids) Algorithm: k-medoids. PAM, a k-medoids algorithm for partitioning based on medoid or central objects. Input: k: the number of clusters, D: a data set containing n objects. Output: A set of k clusters. Method: (1) arbitrarily choose k objects in D as the initial representative objects or seeds; (2) repeat (3) assign each remaining object to the cluster with the nearest representative object; (4) randomly select a non representative object, orandom; (5) compute the total cost, S, of swapping representative object, oj, with orandom; (6) if S < 0 then swap oj with orandom to form the new set of k representative objects; (7) until no change; Ajith G. S: poposir. orgfree. com

Partitioning Methods PAM (Partitioning Around Medoids) Ajith G. S: poposir. orgfree. com

Partitioning Methods PAM (Partitioning Around Medoids) • Comparison • The k-medoids method is more robust than k-means in the presence of noise and outliers, because a medoid is less influenced by outliers or other extreme values than a mean. • The processing cost of K-medoid is high • Both methods require the user to specify k, the number of clusters. • k-median method • The median can be used, resulting in the k-median method, where the median or “middle value” is taken for each ordered attribute. Ajith G. S: poposir. orgfree. com

Partitioning Methods CLARANS • From k-Medoids to CLARANS • k-medoids partitioning algorithm like PAM works effectively for small data sets, but does not scale well for large data sets • A sampling based method called CLARA can be used to deal with large data set Ajith G. S: poposir. orgfree. com

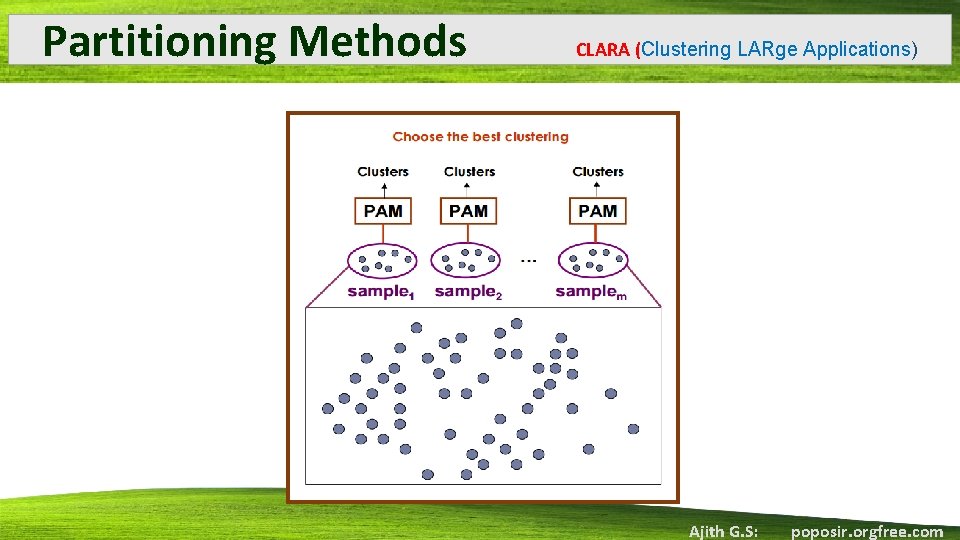
Partitioning Methods CLARA (Clustering LARge Applications) • CLARA draws a sample of the dataset and applies PAM on the sample in order to find the medoids. • A small portion of the actual data is chosen as a representative of the data • Medoiods are then chosen from this sample using PAM • If the sample is fairly the representative of the original data set, the medoids of the sample should approximate the medoids of the entire dataset • Steps • Draw multiple samples of the data set • Apply PAM to each sample • Return the best clustering Ajith G. S: poposir. orgfree. com

Partitioning Methods CLARA (Clustering LARge Applications) Ajith G. S: poposir. orgfree. com

Partitioning Methods CLARA (Clustering LARge Applications) Ajith G. S: poposir. orgfree. com

Partitioning Methods CLARA (Clustering LARge Applications) Properties of CLARA Complexity of each Iteration is: O(ks 2 + k(n-k)) s: the size of the sample k: number of clusters n: number of object PAM finds the best k medoids among a given data, and CLARA finds the best k medoids among the selected samples • Problems • If the best k medoids may not be selected during the sampling process�CLARA will never find the best clustering • If the sampling is biased we cannot have a good clustering • • • Ajith G. S: poposir. orgfree. com

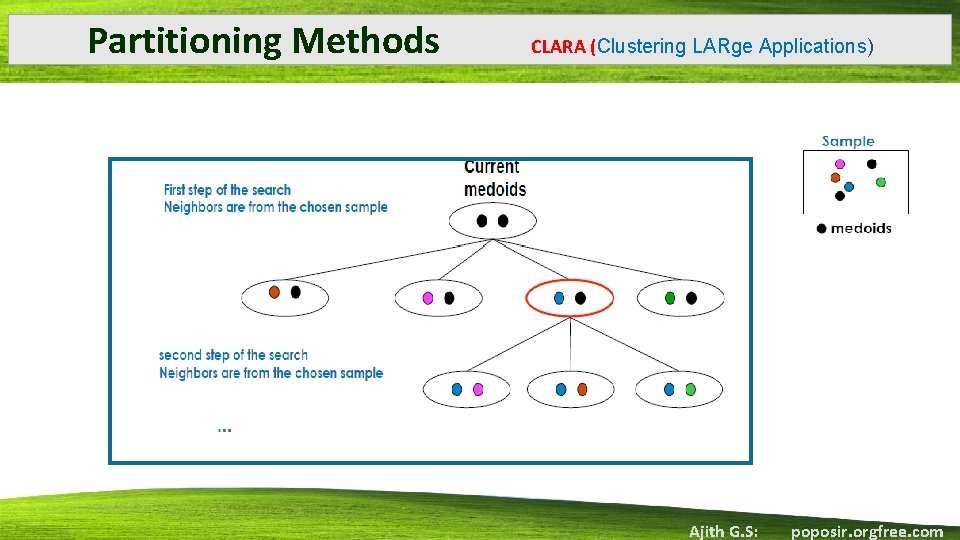
Partitioning Methods CLARANS (“Randomized” CLARA) • To improve the quality and scalability of CLARANS (A Clustering Algorithm based on Randomized Search) • Does not confine itself to any sample at any given time. • CLARANS draws a sample with some randomness in each step of the search. • The clustering process can be viewed s a search through a graph where every node is, a set of k medoids. Ajith G. S: poposir. orgfree. com

Partitioning Methods • • CLARANS (“Randomized” CLARA) PROCEDURE Each node can be assigned a cost that is defined to be the total dissimilarity between every object and the medoid of its cluster. At each step, all neighbours of current node are searched and the least cost node is selected as the solution. The number of neighbours to be randomly sampled is restricted by a user specified parameter. If a better neighbour is found CLARANS moves to the neighbour's node and the process starts again; otherwise, the current clustering produces a local minimum Then CLARANS starts with new randomly selected nodes in search for a new local minimum. Algorithm outputs the best local minimum, that is, the local minimum having the lowest cost. Ajith G. S: poposir. orgfree. com

Partitioning Methods CLARANS (“Randomized” CLARA) • Strengths • More effective than both PAM and CLARA • Finds the most “natural” number of clusters using a silhouette coefficient— a property of an object that specifies how much the object truly belongs to the cluster • It also enables the detection of outliers. • Computational complexity of CLARANS is O(n 2), Ajith G. S: poposir. orgfree. com

Agglomerative Hierarchical Clustering • Bottom-up strategy • Each cluster starts with only one object • Clusters are merged into larger and larger clusters until: • All the objects are in a single cluster • Certain termination conditions are satisfied Ajith G. S: poposir. orgfree. com

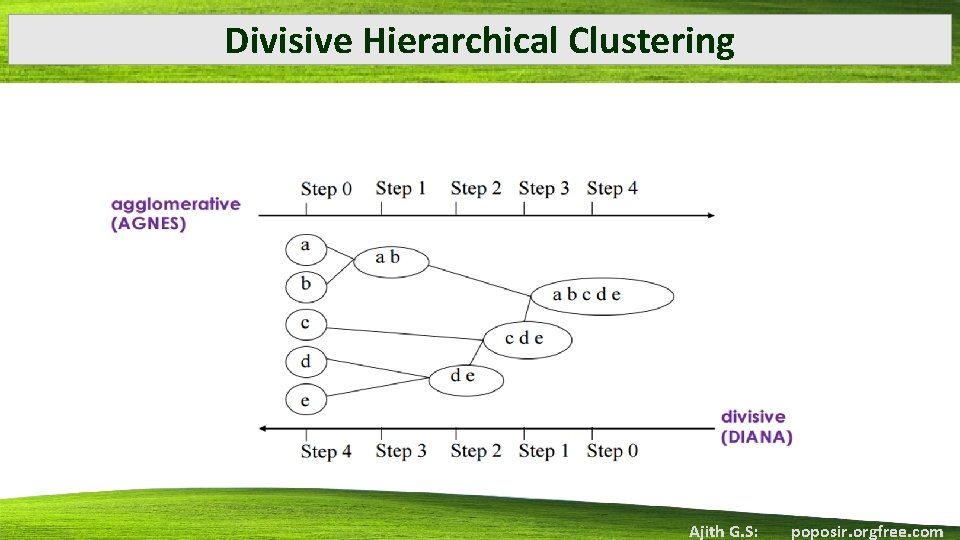
Divisive Hierarchical Clustering • Top-down strategy • Start with all objects in one cluster • Clusters are subdivided into smaller and smaller clusters until: • Each object forms a cluster on its own • Certain termination conditions are satisfied Ajith G. S: poposir. orgfree. com

Divisive Hierarchical Clustering Ajith G. S: poposir. orgfree. com

AGNES DIANA • AGNES(AGglomerative NESting) • Clusters C 1 and C 2 may be merged if an object in C 1 and an object in C 2 form the minimum Euclidean distance between any two objects from different clusters • DIANA (DIvisive ANAlysis) • A cluster is split according to some principle, e. g. , the maximum Euclidian distance between the closest neighboring objects in the cluster Ajith G. S: poposir. orgfree. com

Distance Calculation Methods Between Clusters • First measure: Minimum distance • • |p-p’| is the distance between two objects p and p’ An algorithm that uses the minimum distance to measure the distance between clusters is called sometimes nearest-neighbor clustering algorithm If the clustering process terminates when the minimum distance between nearest clusters exceeds an arbitrary threshold, it is called single-linkage algorithm An agglomerative algorithm that uses the minimum distance measure is also called minimal spanning tree algorithm • • Ajith G. S: poposir. orgfree. com

Distance Calculation Methods Between Clusters • Second measure: Maximum distance • |p-p’| is the distance between two objects p and p’ • An algorithm that uses the maximum distance to measure the distance between clusters is called as farthest-neighbor clustering algorithm • If the clustering process terminates when the maximum distance between nearest clusters exceeds an arbitrary threshold, called as complete-linkage algorithm Ajith G. S: poposir. orgfree. com

Distance Calculation Methods Between Clusters • Minimum and maximum distances are extreme implying that they are overly sensitive to outliers or noisy data • Third measure: Mean distance • mi and mj are the means for cluster Ci and Cj respectively Ajith G. S: poposir. orgfree. com

Distance Calculation Methods Between Clusters • Fourth measure: Average distance • |p-p’| is the distance between two objects p and p’ • ni and nj are the number of objects in cluster Ci and Cj respectively • Mean is difficult to compute for categorical data Ajith G. S: poposir. orgfree. com

Challenges & Solutions • It is difficult to select merge or split points • No backtracking • Hierarchical clustering does not scale well: examines a good number of objects before any decision of split or merge • One promising directions to solve these problems is to combine hierarchical clustering with other clustering techniques: multiple-phase clustering Ajith G. S: poposir. orgfree. com

BIRCH (Balanced Iterative Reducing and Clustering Using Hierarchies ) • BIRCH is designed for clustering a large amount of numerical data • It overcomes the two difficulties of agglomerative clustering methods: (1) scalability and (2) the inability to undo what was done in the previous step. • BIRCH introduces two concepts, • Clustering feature (CF) and • Clustering feature tree (CF-Tree) Ajith G. S: poposir. orgfree. com

BIRCH: Key Components • Clustering Feature (CF) • Summarizes the given cluster representations. • Helps to achieve good speed and scalability in large databases. • Used to compute centroids, and measure the compactness and distance of clusters. Ajith G. S: poposir. orgfree. com

BIRCH (Balanced Iterative Reducing and Clustering Using Hierarchies ) • • Clustering Feature (CF) Distance Measures • • • R : average distance from member objects to the centroid D : average pairwise distance within a cluster Both R and D reflect the tightness of the cluster around the centroid. Ajith G. S: poposir. orgfree. com

BIRCH (Balanced Iterative Reducing and Clustering Using Hierarchies ) • Clustering Feature (CF) • A clustering feature (CF) is a three-dimensional vector summarizing information about clusters of objects. • Given n d-dimensional objects or points in a cluster, { xi }, then the CF of the cluster is defined as • n number of points in the cluster • LS linear sum of the n points • SS square sum of the data points • Clustering features are additive. Ajith G. S: poposir. orgfree. com

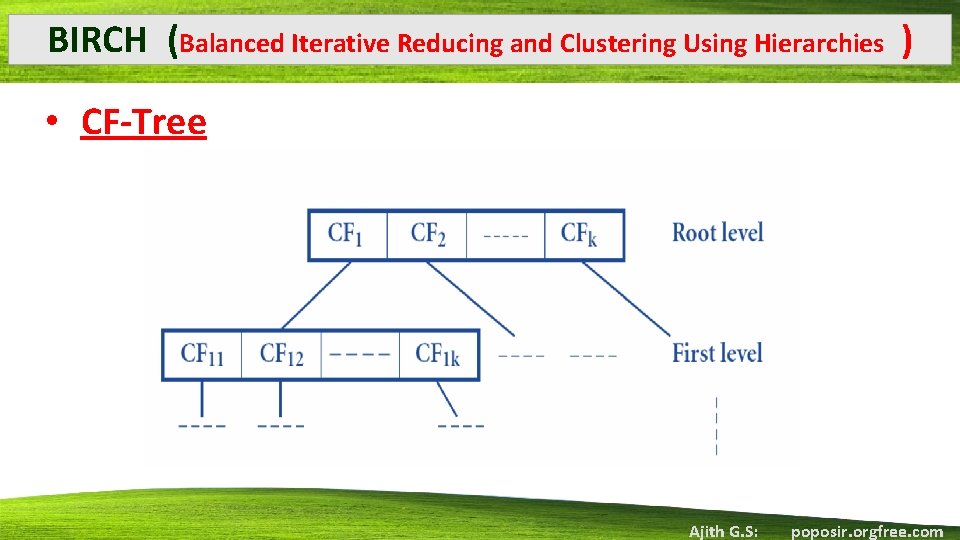
BIRCH (Balanced Iterative Reducing and Clustering Using Hierarchies ) CF-Tree height-balanced tree. stores clustering features for a hierarchical clustering. has 2 parameters: Branching factor, B Threshold, T Branching Factor- specifies the maximum number of children per non-leaf node. • Threshold T - specifies the maximum diameter of sub clusters stored at the leaf nodes of the tree. • These two parameters influence the size of the resulting tree. • • Ajith G. S: poposir. orgfree. com

Partitioning Methods CLARANS Ajith G. S: poposir. orgfree. com

BIRCH (Balanced Iterative Reducing and Clustering Using Hierarchies ) • CF-Tree Ajith G. S: poposir. orgfree. com

BIRCH-Phases • BIRCH applies a multiphase clustering technique • a single scan of the data set yields a basic good clustering, • one or more additional scans can (optionally) be used to further improve the quality. • The primary phases are: • Phase 1: BIRCH scans the database to build an initial inmemory CF tree a multilevel compression of the data • Phase 2: BIRCH applies a (selected) clustering algorithm to cluster the leaf nodes of the CF tree, which removes sparse clusters as outliers and groups dense clusters into larger ones. Ajith G. S: poposir. orgfree. com

BIRCH-Phases • For Phase 1, the CF tree is built dynamically as objects are inserted. • The object is inserted into the closest leaf entry (subcluster). • If the diameter of the sub-cluster stored in the leaf node after insertion is larger than the threshold value, then the leaf node and possibly other nodes are split. • After the insertion of the new object, information about it is passed toward the root of the tree. Ajith G. S: poposir. orgfree. com