A Calculus of Atomic Actions Serdar Tasiran Koc

A Calculus of Atomic Actions Serdar Tasiran Koc University, Istanbul, Turkey Tayfun Elmas Shaz Qadeer Koc University Microsoft Research

Problem • Verifying assertions in concurrent programs – Local conditions, program invariants, data integrity, absence of null pointer dereferences, . . . static void transfer(Account from, Account to, int amount) { assert (from != null && to != null); assert (from. balance >= amount); old_total : = from. balance + to. balance; tmp : = from. balance; from. balance : = tmp – amount; tmp : = to. balance; to. balance : = tmp + amount; assert (from. balance + to. balance == old_total); } 2

Our Approach: QED • Proof method for verifying assertions • Implementation: The QED tool • Central idea: Atomicity • Allows separation of concerns – Concurrency: Non-interference, synchronization mechanism – Data: Sequential reasoning within atomic blocks to prove assertions • QED proof rules: Program transformation steps – Abstraction: To increase “non-interference” between actions – Reduction: Prove bigger blocks atomic – Grow atomic blocks • Sequential reasoning within atomic blocks 3

Outline • Motivating example • Proof method • Experience • Full example: Multiset 4

5 Example – inc (): int t; acquire (lock); t = x; t = t + 1; x = t; release(lock); Main: assume (x == 0); inc() || assert (x == 2) inc()

Proof by Owicki-Gries A: <B@L 0=>x=0, B@L 5=>x=1> B: <A@L 0=>x=0, A@L 5=>x=1> L 0: acquire(l); <B@L 0=>x=0, B@L 5=>x=1, held(l, A)> <A@L 0=>x=0, A@L 5=>x=1, held(l, B)> L 1: t : = x; <B@L 0=>x=0, B@L 5=>x=1, held(l, A), t=x> <A@L 0=>x=0, A@L 5=>x=1, held(l, B), t=x> L 2: t : = t + 1; || 6 L 2: t : = t + 1; <B@L 0=>x=0, B@L 5=>x=1, held(l, A), t=x+1> <A@L 0=>x=0, A@L 5=>x=1, held(l, B), t=x+1> L 3: x : = t; <B@L 0=>x=1, B@L 5=>x=2, held(l, A)> <A@L 0=>x=1, A@L 5=>x=2, held(l, B)> L 4: release(l) <B@L 0=>x=1, B@L 5=>x=2> <A@L 0=>x=1, A@L 5=>x=2>

Reduction • α right mover (R) if for every execution ξ = ……. α β ……. ξ’ = ……. β α ……. is equivalent to ξ • Static check for α being a right mover: – For all actions β in program, is α β always “simulated” by β α? – Easy case: β cannot follow α • Example: α = β = lock. acquire() • Reduction: Atomic patterns – RRRR N LLLLL – RRRRR – LLLLL –. . .

Proof by reduction - 1 inc (): int t; acquire (lock); t = x; inc (): int t; R acquire (lock); t = x; B REDUCE-SEQUENTIAL t=t+1 B t=t+1 x = t; B x = t; release(lock); L release(lock); inc (): x = x + 1; 8

9 Proof by reduction - 2 assume (x == 0); B B inc() || assume (x == 0); inc() x=x+1 assert (x == 2) || x=x+1 assert (x == 2) INLINE-CALL REDUCE-PARALLEL x = x + 1; assert (x == 2)

Non-blocking increment inc (): int t; while(true) { t = x; if(CAS(x, t, t+1)) break; } CAS(x, t, t + 1): assume (x == t); x = t + 1; return true; □ assume (x != t); return false; 10

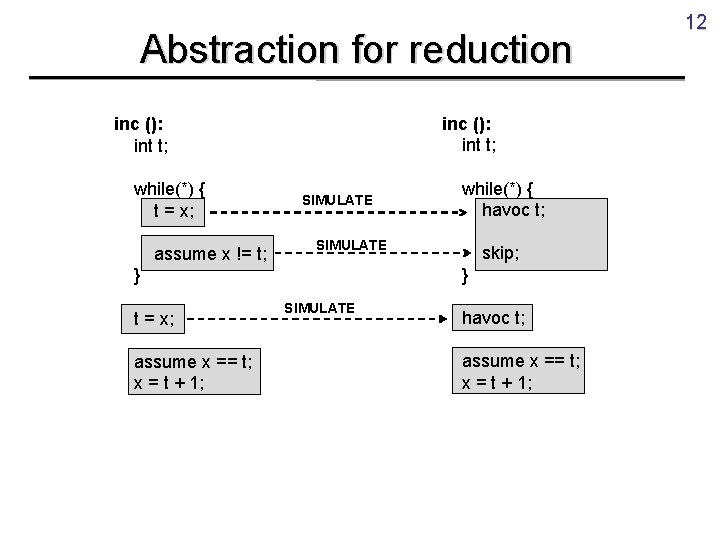
Abstraction for reduction inc (): int t; while(true) { t = x; if(CAS(x, t, t+1)) break; } inc (): int t; while(*) { t = x; assume x != t; } t = x; assume x == t; x = t + 1; 11

Abstraction for reduction inc (): int t; while(*) { t = x; assume x != t; SIMULATE assume x == t; x = t + 1; skip; } } t = x; while(*) { havoc t; SIMULATE havoc t; assume x == t; x = t + 1; 12

Proof by reduction inc (): int t; while(*) { havoc t; skip; REDUCE-LOOP havoc t; B } havoc t; assume x == t; x : = t + 1; havoc t; x : = x + 1; 13

14 Action. PL Syntax: Global variables Program: Program’s main body Procedure bodies

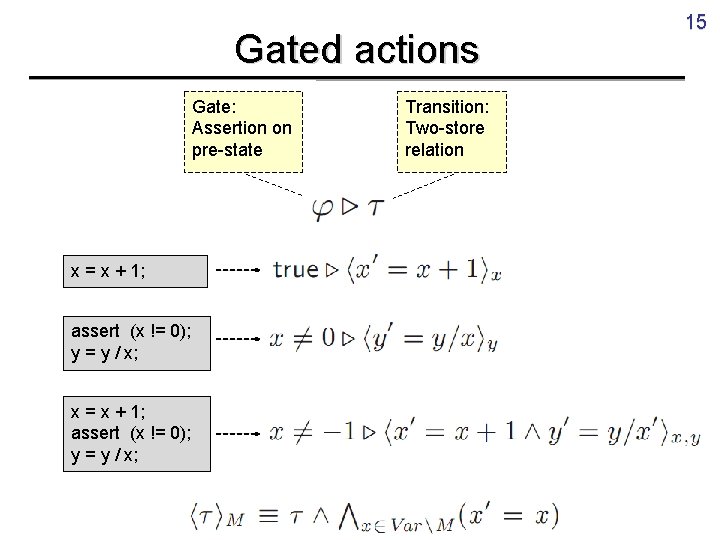
Gated actions Gate: Assertion on pre-state x = x + 1; assert (x != 0); y = y / x; Transition: Two-store relation 15

Semantics of Action. PL Current store Execution: Current dynamic statement Atomic transitions: Pre-store satisfies assertion Pre- and post-store satisfies transition Pre-store violates assertion 16

Operational semantics 17

Proof method Proof context Current program Program invariant (proof ensures this) Each execution starts from invariant Each transition preserves invariant Proof step: Governed by a proof rule May strengthen invariant May rewrite program 18

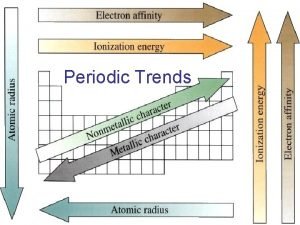
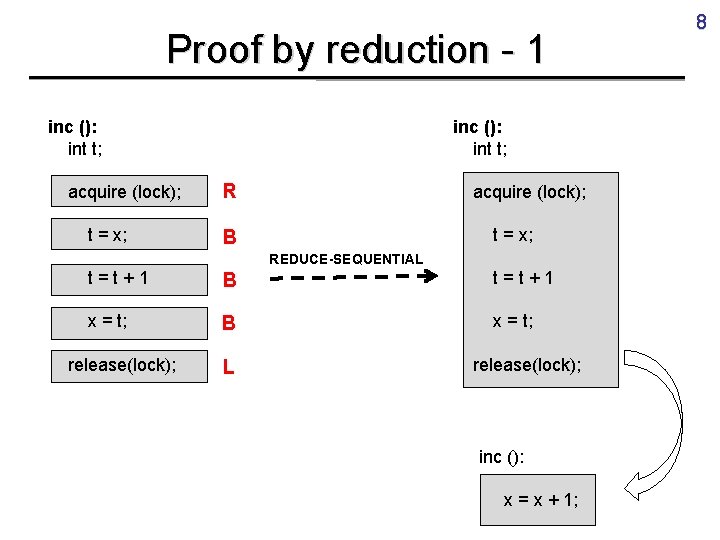
19 Soundness • Theorem [Preservation] – Each proof step: • Let. If goes from to – goes wrong from skip, error, other dyn. stmt. then , or • Theorem [Soundness] – Each proof: • If goes from to – goes wrong from such that , or then:

Validating assertions Proof succeeds if For all in , holds. Verifying each assertion is local & sequential 20

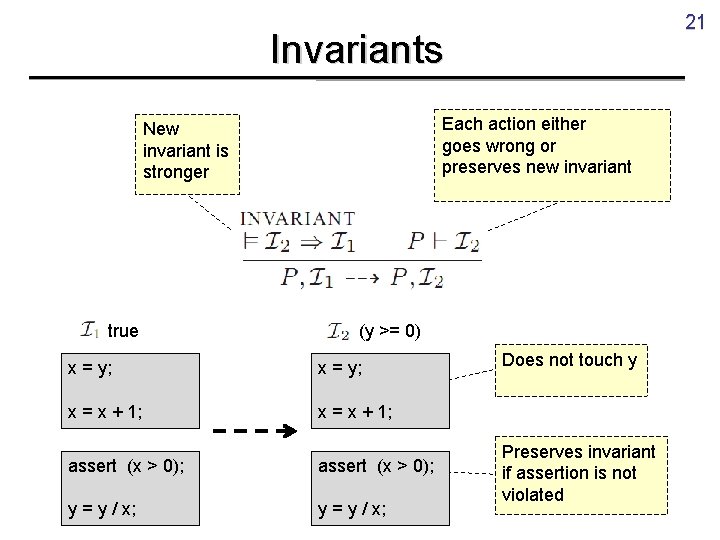
21 Invariants Each action either goes wrong or preserves new invariant New invariant is stronger true (y >= 0) x = y; x = x + 1; assert (x > 0); y = y / x; Does not touch y Preserves invariant if assertion is not violated

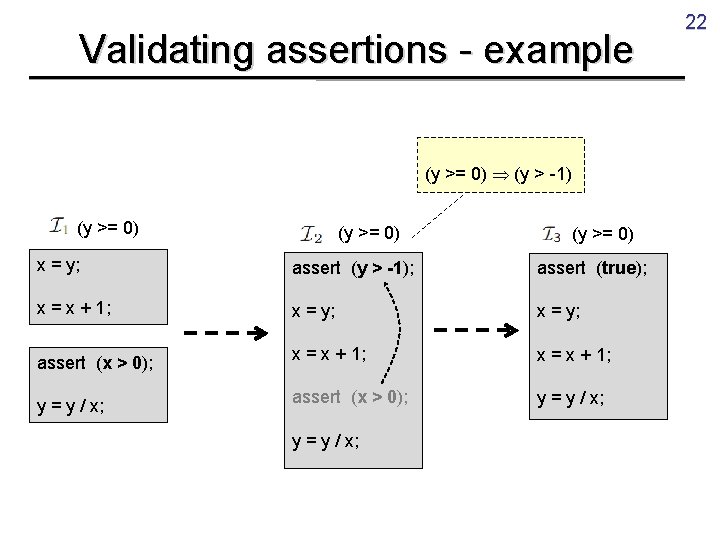
Validating assertions - example (y >= 0) (y > -1) (y >= 0) x = y; assert (y > -1); assert (true); x = x + 1; x = y; assert (x > 0); x = x + 1; y = y / x; assert (x > 0); y = y / x; 22

Auxiliary variables inc (): int t; acquire (lock); a : = tid; t : = x; t : = t + 1 x : = t; release(lock); a : = 0; 23

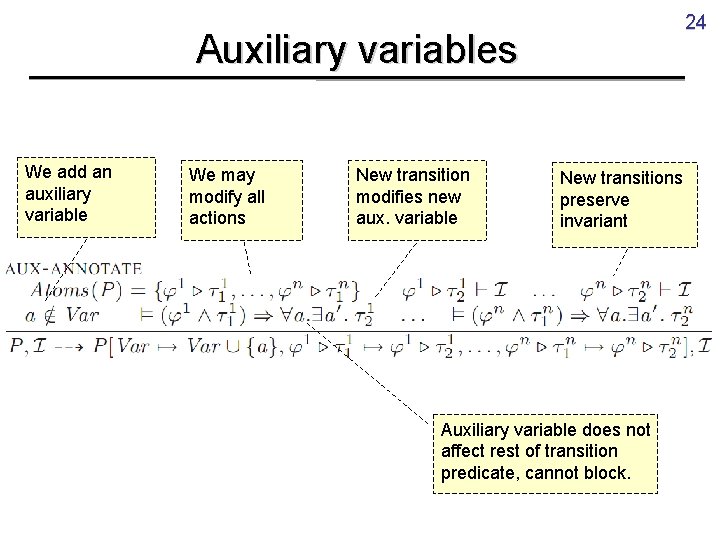
24 Auxiliary variables We add an auxiliary variable We may modify all actions New transition modifies new aux. variable New transitions preserve invariant Auxiliary variable does not affect rest of transition predicate, cannot block.

25 Simulation From each store satisfying invariant, goes wrong or simulates. New action preserves invariant New action simulates the former Adding behaviors that go wrong y = y / x; assert (x > 0); y = y / x; Adding non-determinism if (x == 1) y = y + 1; if (*) y = y + 1;

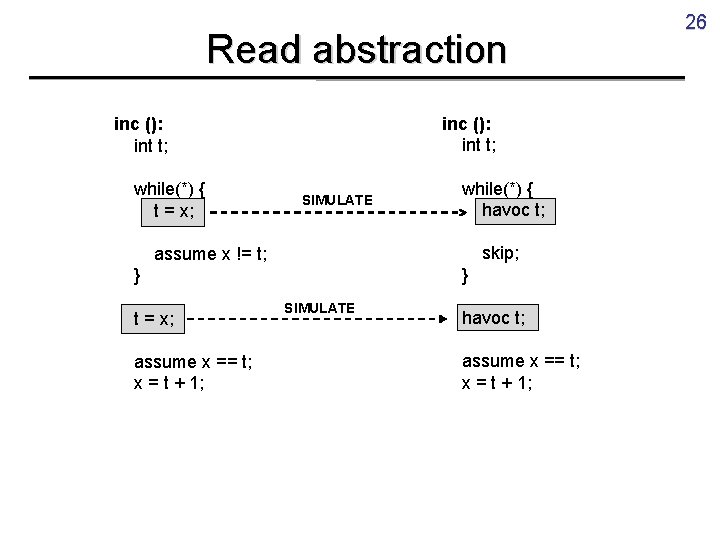
Read abstraction inc (): int t; while(*) { t = x; SIMULATE while(*) { havoc t; skip; assume x != t; } } t = x; assume x == t; x = t + 1; SIMULATE havoc t; assume x == t; x = t + 1; 26

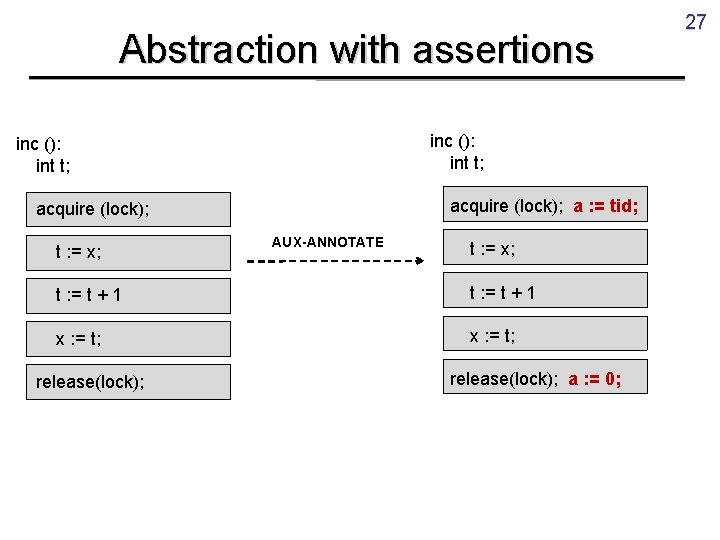
Abstraction with assertions inc (): int t; acquire (lock); a : = tid; acquire (lock); t : = x; AUX-ANNOTATE t : = x; t : = t + 1 x : = t; release(lock); a : = 0; 27

Abstraction with assertions inc (): int t; acquire (lock); a : = tid; t : = x; SIMULATE assert a == tid; t : = x; t : = t + 1 assert a == tid; t : = t + 1 x : = t; assert a == tid; x : = t; release(lock); a : = 0; 28 assert a == tid; release(lock); a : = 0;

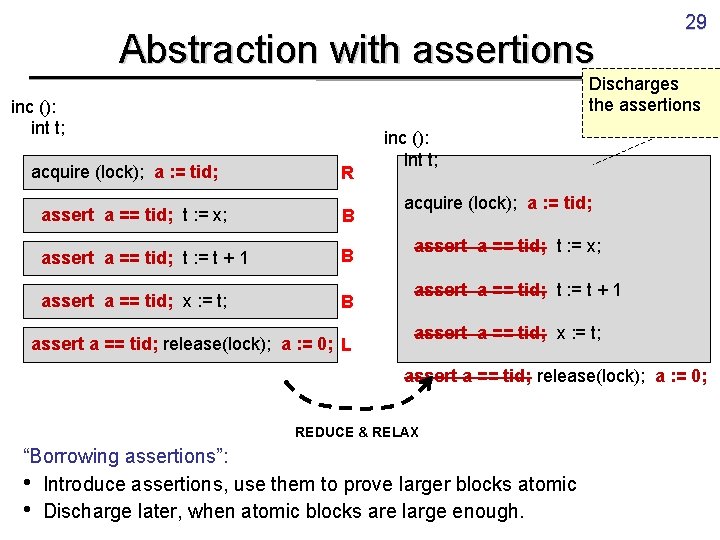
Abstraction with assertions Discharges the assertions inc (): int t; acquire (lock); a : = tid; R assert a == tid; t : = x; B assert a == tid; t : = t + 1 B assert a == tid; x : = t; 29 B assert a == tid; release(lock); a : = 0; L inc (): int t; acquire (lock); a : = tid; assert a == tid; t : = x; assert a == tid; t : = t + 1 assert a == tid; x : = t; assert a == tid; release(lock); a : = 0; REDUCE & RELAX “Borrowing assertions”: • Introduce assertions, use them to prove larger blocks atomic • Discharge later, when atomic blocks are large enough.

Reduction Moving to the left makes the execution either - go to same end state or - makes execution go wrong Actions executed by different threads 30

Reduce - sequential 31

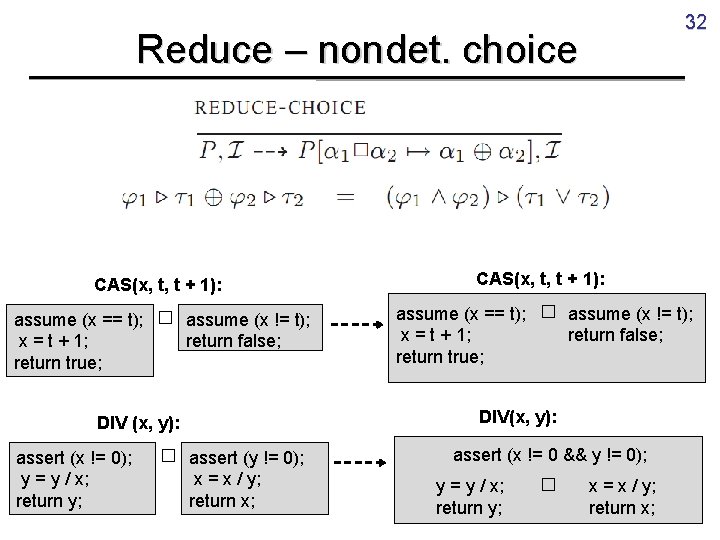
32 Reduce – nondet. choice CAS(x, t, t + 1): assume (x == t); x = t + 1; return true; □ assume (x != t); return false; □ assume (x == t); x = t + 1; return true; □ assume (x != t); return false; DIV(x, y): DIV (x, y): assert (x != 0); y = y / x; return y; CAS(x, t, t + 1): assert (y != 0); x = x / y; return x; assert (x != 0 && y != 0); y = y / x; return y; □ x = x / y; return x;

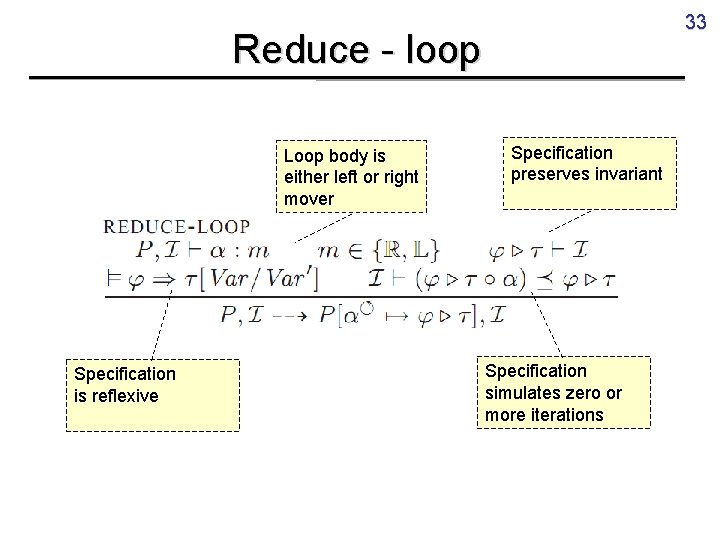
33 Reduce - loop Loop body is either left or right mover Specification is reflexive Specification preserves invariant Specification simulates zero or more iterations

34 Reduce - parallel Explicitly expand the parallel statement to its possible executions Reduces parallel composition to sequential composition

Experience • Implementation: Spec# Boogie. PL QED – Generate verification condition (VC) for validity of each proof step – VC fed to the Z 3 theorem prover • Purity benchmarks [Flanagan et. al, 2005] • Non-blocking algorithms – Obstruction-free deque [Herlihy et. al. 2003] – Non-blocking stack [Michael, 2004] – Bakery [Lamport, 1974] • Multiset • Conclusion: – Iteration of abstraction and reduction is powerful – Growing atomic code blocks useful approach 35

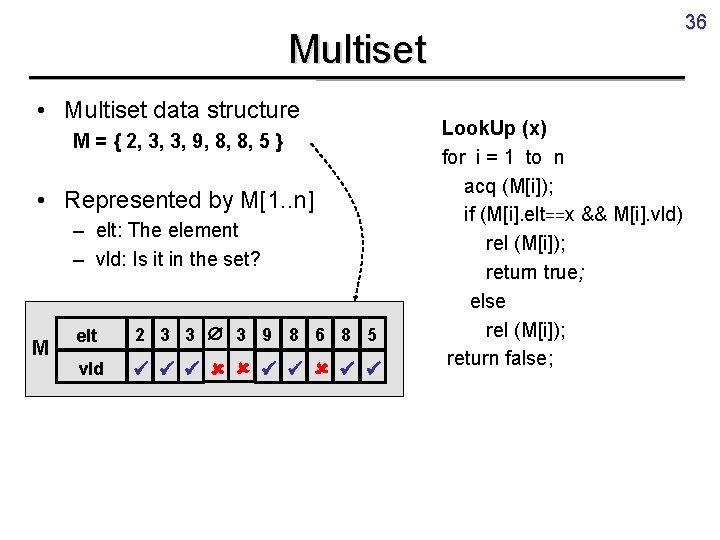
36 Multiset • Multiset data structure M = { 2, 3, 3, 9, 8, 8, 5 } • Represented by M[1. . n] – elt: The element – vld: Is it in the set? M elt 2 3 3 3 9 8 6 8 5 vld Look. Up (x) for i = 1 to n acq (M[i]); if (M[i]. elt==x && M[i]. vld) rel (M[i]); return true; else rel (M[i]); return false;

Find. Slot and Insert. Pair Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); if (M[i]. elt == null) { M[i]. elt= x; rel (M[i]); r = i; } else { rel (M[i]); } i = i + 1; } return r; Insert. Pair (x, y) i = Find. Slot (x); if (i == -1) { return failure; } j = Find. Slot (y); if (j == -1) { M[i]. elt= null; return failure; } acq (M[i]) acq (M[j]) M[i]. vld = true; M[j]. vld = true; rel (M[i]); rel (M[j]); return success;

Rewriting the “if” statement Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); if (M[i]. elt == null) { M[i]. elt= x; rel (M[i]); r = i; } else { rel (M[i]); } i = i + 1; } return r; Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); assume (M[i]. elt == null); M[i]. elt= x; rel (M[i]); r = i; □ acq (A[i]); assume (M[i] != null); rel (M[i]); i = i + 1; } return r; 38

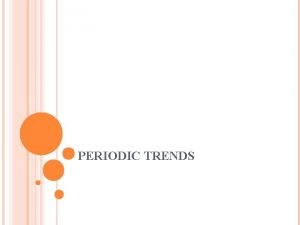
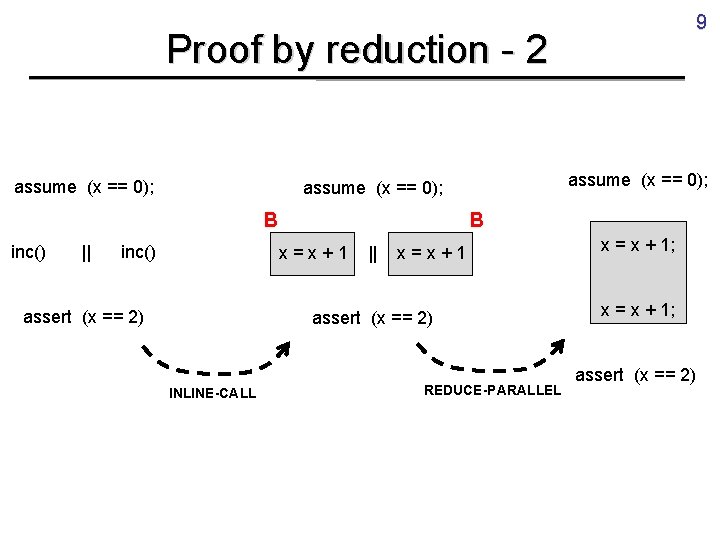
39 mutex (M[i]. lock == true) Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); assume (M[i]. elt == null); M[i]. elt= x; rel (M[i]); r = i; □ acq (A[i]); assume (M[i] != null); rel (M[i]); i = i + 1; } return r; REDUCE Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); assume (M[i]. elt == null); M[i]. elt= x; rel (M[i]); r = i; □ acq (A[i]); assume (M[i] != null); rel (M[i]); i = i + 1; } return r;

40 Read abstraction Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); assume (M[i]. elt == null); M[i]. elt= x; rel (M[i]); r = i; □ □ acq (A[i]); assume (M[i] != null); rel (M[i]); i = i + 1; } return r; SIMULATE acq (A[i]); skip rel (M[i]); i = i + 1; } return r;

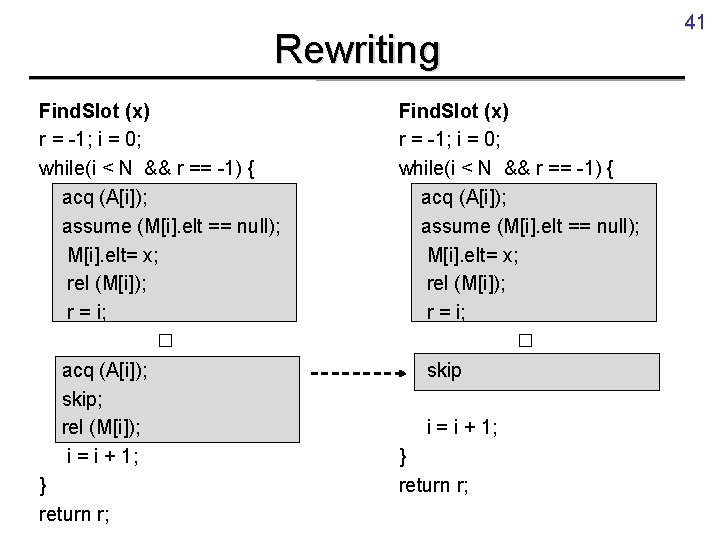
41 Rewriting Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); assume (M[i]. elt == null); M[i]. elt= x; rel (M[i]); r = i; □ acq (A[i]); skip; rel (M[i]); i = i + 1; } return r; Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); assume (M[i]. elt == null); M[i]. elt= x; rel (M[i]); r = i; □ skip i = i + 1; } return r;

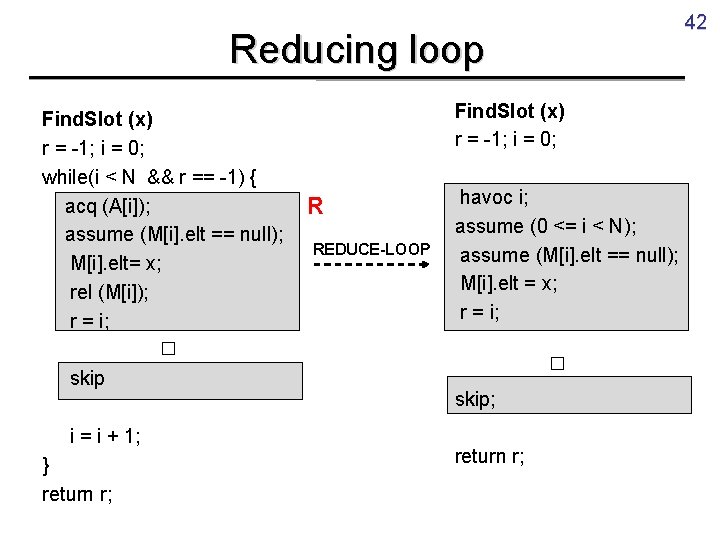
42 Reducing loop Find. Slot (x) r = -1; i = 0; while(i < N && r == -1) { acq (A[i]); assume (M[i]. elt == null); M[i]. elt= x; rel (M[i]); r = i; Find. Slot (x) r = -1; i = 0; R REDUCE-LOOP havoc i; assume (0 <= i < N); assume (M[i]. elt == null); M[i]. elt = x; r = i; □ skip i = i + 1; } return r; □ skip; return r;

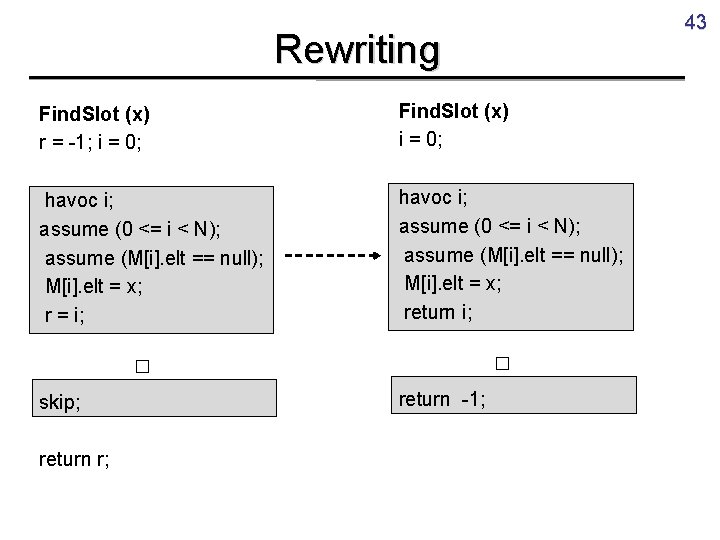
43 Rewriting Find. Slot (x) r = -1; i = 0; Find. Slot (x) i = 0; havoc i; assume (0 <= i < N); assume (M[i]. elt == null); M[i]. elt = x; r = i; havoc i; assume (0 <= i < N); assume (M[i]. elt == null); M[i]. elt = x; return i; □ □ skip; return r; return -1;

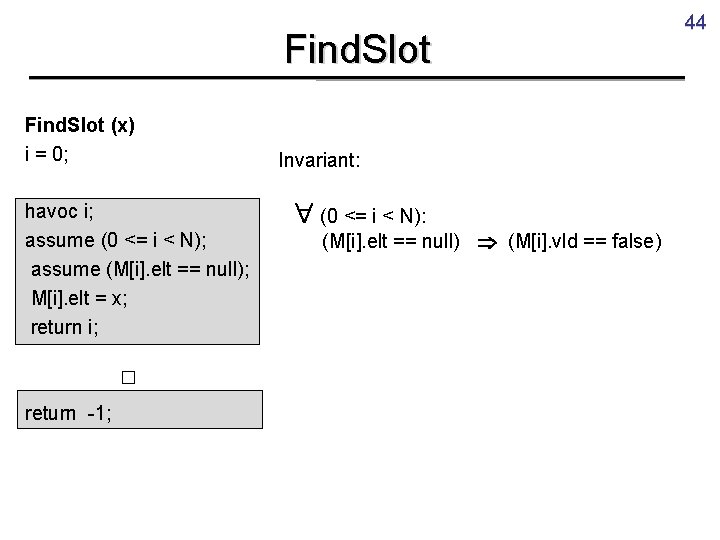
Find. Slot (x) i = 0; havoc i; assume (0 <= i < N); assume (M[i]. elt == null); M[i]. elt = x; return i; □ return -1; Invariant: (0 <= i < N): (M[i]. elt == null) (M[i]. vld == false) 44

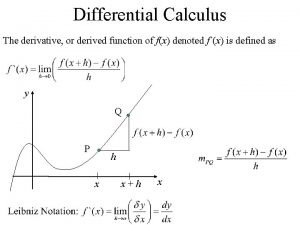
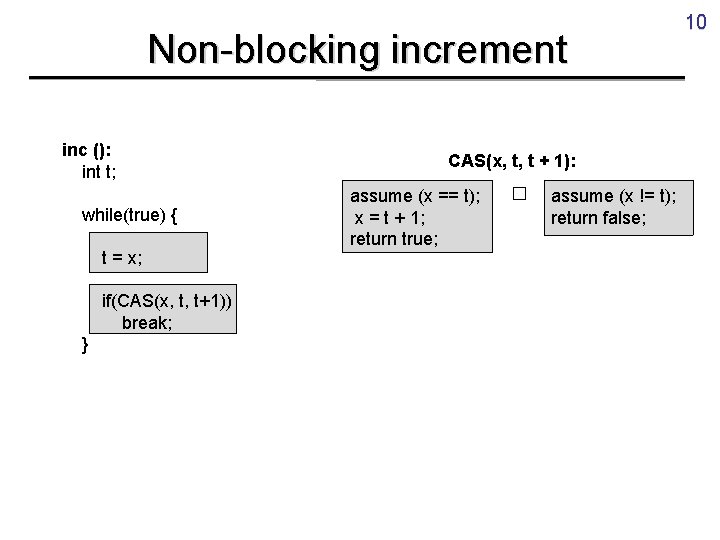
mutex (M[i]. elt != null && M[i] == false) Insert. Pair (x, y) i = Find. Slot (x); if (i == -1) return failure; j = Find. Slot (y); if (j == -1) M[i]. elt= null; return failure; acq (M[i]) acq (M[j]) M[i]. vld = true; M[j]. vld = true; rel (M[i]); rel (M[j]); return success; SIMULATE R i = Find. Slot (x); if (i == -1) return failure; a[i] = tid; R j = Find. Slot (y); if (j == -1) M[i]. elt= null; return failure; a[j] = tid; acq (M[i]) acq (M[j]) M[i]. vld = true; M[j]. vld = true; rel (M[i]); rel (M[j]); return success; 45

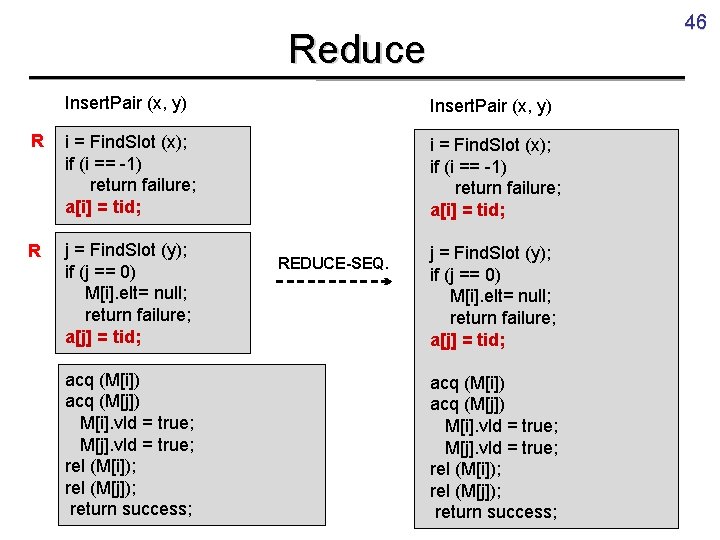
46 Reduce Insert. Pair (x, y) R i = Find. Slot (x); if (i == -1) return failure; a[i] = tid; R j = Find. Slot (y); if (j == 0) M[i]. elt= null; return failure; a[j] = tid; acq (M[i]) acq (M[j]) M[i]. vld = true; M[j]. vld = true; rel (M[i]); rel (M[j]); return success; REDUCE-SEQ. j = Find. Slot (y); if (j == 0) M[i]. elt= null; return failure; a[j] = tid; acq (M[i]) acq (M[j]) M[i]. vld = true; M[j]. vld = true; rel (M[i]); rel (M[j]); return success;

Future work • Proof script templates for encoding synchronization idioms – – Guidelines for adding annotation and code transformations Mutual-exclusion, readers/writers lock, barriers Barriers, event synchronization Optimistic concurrency • Statically checking serializability of marked-atomic blocks • Verifying STM implementations using QED 47

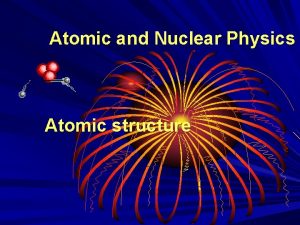
Delete (x) for i = 1 to n acq (M[i]); if (M[i]. elt==x && M[i]. vld) M[i]. elt = null; M[i]. vld = false; rel(M[i]); return true; else rel(M[i]); return false

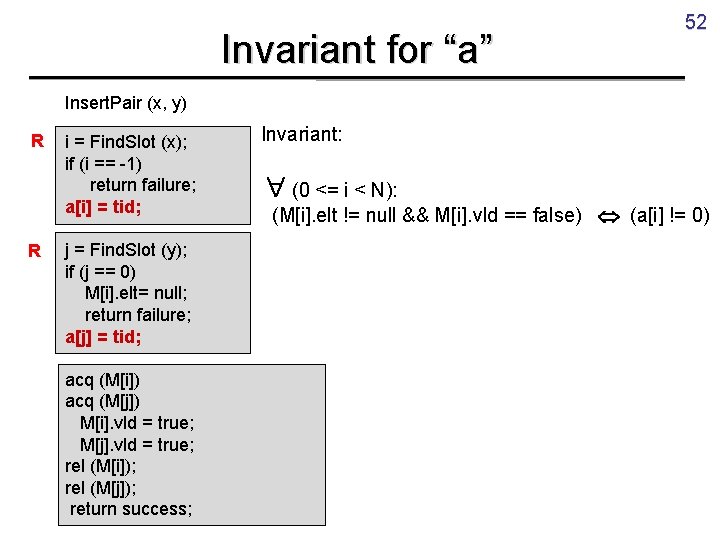
Invariant for “a” 52 Insert. Pair (x, y) R R i = Find. Slot (x); if (i == -1) return failure; a[i] = tid; j = Find. Slot (y); if (j == 0) M[i]. elt= null; return failure; a[j] = tid; acq (M[i]) acq (M[j]) M[i]. vld = true; M[j]. vld = true; rel (M[i]); rel (M[j]); return success; Invariant: (0 <= i < N): (M[i]. elt != null && M[i]. vld == false) (a[i] != 0)