A brief introduction to information theory 1 Example

A brief introduction to information theory 1

Example uses of information theory in bioinformatics • To derive sequence weights in HMM and profile construction. – UCSC SAM-T 98 HMM construction for remote homolog detection; target information content relative to the background distribution (Park et al, JMB 1998) • Scoring functions for HMM-HMM (or profile-profile) comparison and alignment. Examples: – Agglomerative clustering of proteins into a hierarchical tree: symmetrized KL divergence between profiles (Brown et al. PCBI, 2007) – Benchmarking profile-profile scoring functions vs structural alignments (Edgar and Sjölander) • • Clustering techniques involving measures of similarity between statistical models for individual classes Encoding cost – SCI-PHY encoding cost cut of tree into subtrees for subfamily identification (Brown et al. ) • Prediction of functional sites based on entropy measures – INTREPID (Jensen-Shannon divergence) 1. 2. 3. 4. Brown DP, Krishnamurthy N, Sjölander K, "Automated Protein Subfamily Identification and Classification, " PLo. S Computational Biology 2007, 3(8): e 160 doi: 10. 1371/journal. pcbi. 0030160. Edgar, R. and Sjölander, K. , "A comparison of scoring functions for protein sequence profile alignment, " Bioinformatics 2004 May 22; 20(8): 1301 -8 Sankararaman S and Sjölander K, "INTREPID - INformation-theoretic TREe traversal for Protein functional site IDentification, " Bioinformatics 2008; doi: 2 10. 1093/bioinformatics/btn 474 Park et al, “Sequence comparisons using multiple sequences detect three times as many remote homologues as pairwise methods” JMB 1998

Shannon Entropy https: //en. wikipedia. org/wiki/Entropy_(information_theory) 3

The expected value of the information contained in each message https: //en. wikipedia. org/wiki/Entropy_(information_theory) 4

Entropy in thermodynamics and information theory https: //en. wikipedia. org/wiki/Entropy_in_thermodynamics_and_information_theory 5

https: //en. wikipedia. org/wiki/Entropy_(information_theory) 6

Encoding cost and Shannon Entropy https: //en. wikipedia. org/wiki/Entropy_encoding 7

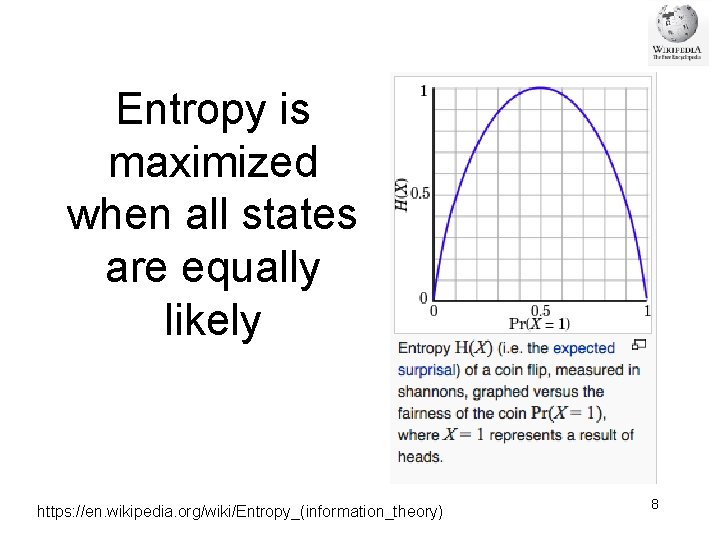
Entropy is maximized when all states are equally likely https: //en. wikipedia. org/wiki/Entropy_(information_theory) 8

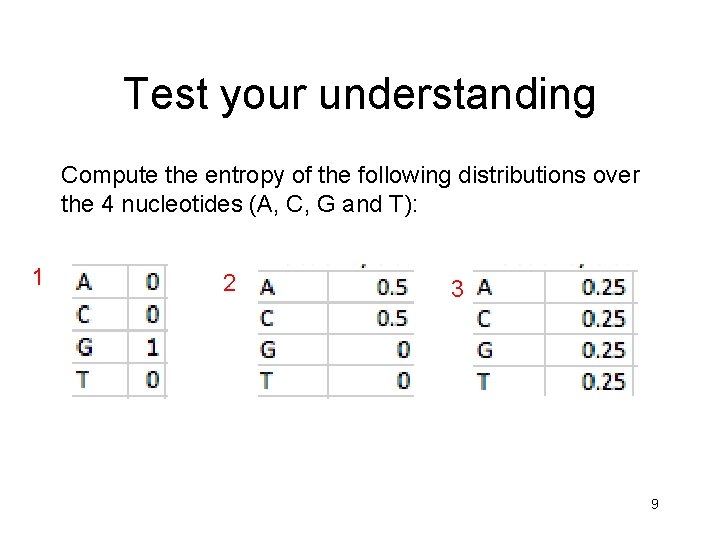
Test your understanding Compute the entropy of the following distributions over the 4 nucleotides (A, C, G and T): 1 2 3 9

Estimating the distance (or divergence) between distributions • Example uses: – Profile-profile scoring (or HMM-HMM scoring) – Aligning two profiles (or HMMs) to each other – Assignment of a cluster of data to existing classes • Notes: – Many “distance” functions are not true distance metrics – Some functions can blow up (or be undefined) when distributions include some very small values 10

Distance metrics https: //en. wikipedia. org/wiki/Distance 11

Relative Entropy (aka Kullback-Leibler divergence) http: //mathworld. wolfram. com/Relative. Entropy. html 12

Kullback-Leibler Divergence 13 https: //en. wikipedia. org/wiki/Kullback–Leibler_divergence

Limitations of KL divergence • Any zero probabilities in q can cause D(p||q) to be undefined. – Also sensitive to very small values in q – Major problem in cases where dataset sizes are small or data are biased • Not symmetric • Not a true metric • These problems are (mostly) resolved in the Jensen-Shannon (JS) divergence 14

An general form for symmetrized divergence 15

Jensen-Shannon Divergence https: //en. wikipedia. org/wiki/Jensen–Shannon_divergence 16

Some comments on the relative entropy (Kullback-Leibler divergence) D (p||q) and Jensen-Shannon divergence • KL divergence is undefined if any elements of q have probability zero – Cannot normally be applied to raw frequencies – Smoothing functions (generalization) can be applied first (but may affect inferences) • KL is not symmetric (but can be symmetrized easily) • Jensen-Shannon is a smoothed and symmetrized form of RE 17

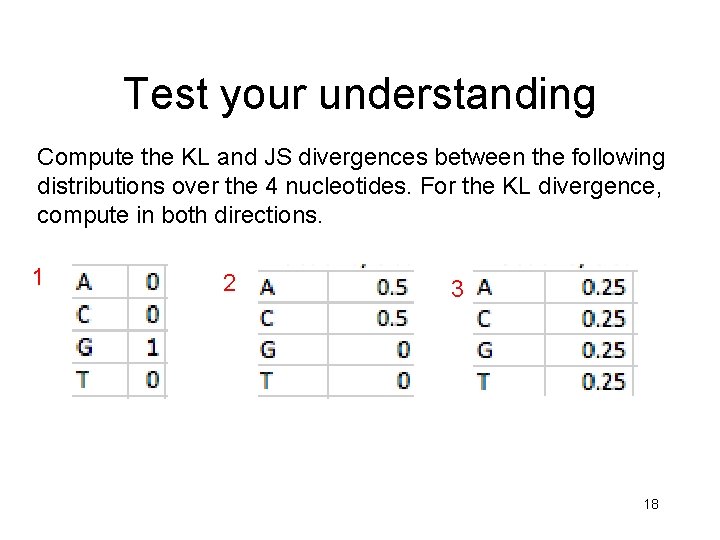
Test your understanding Compute the KL and JS divergences between the following distributions over the 4 nucleotides. For the KL divergence, compute in both directions. 1 2 3 18

Recommended reading • https: //en. wikipedia. org/wiki/Entropy_(information_theory ) • http: //stefansavev. com/blog/beyond-cosine-similarity/ • https: //liorpachter. wordpress. com/tag/jensen-shannondivergence/ • https: //en. wikipedia. org/wiki/Distance • https: //en. wikipedia. org/wiki/Entropy_encoding 19