A brief history of model checking Ken Mc

A brief history of model checking Ken Mc. Millan Cadence Berkeley Labs mcmillan@cadence. com

Outline • Part I -- Introduction to model checking – Automatic formal verification of finite-state systems – Applications • Commercial hardware design • Avionics, chemical plant control, automotive, etc. • Part II -- A brief history of model checking – Influence of many abstract ideas from logic on the development of model checking

The Verification Problem • Debugging chips by simulation. . . – consumes greater than half of design time, – is unreliable • “Escapes” can cost up to $500 M, – is increasing in cost as chip densities scale up

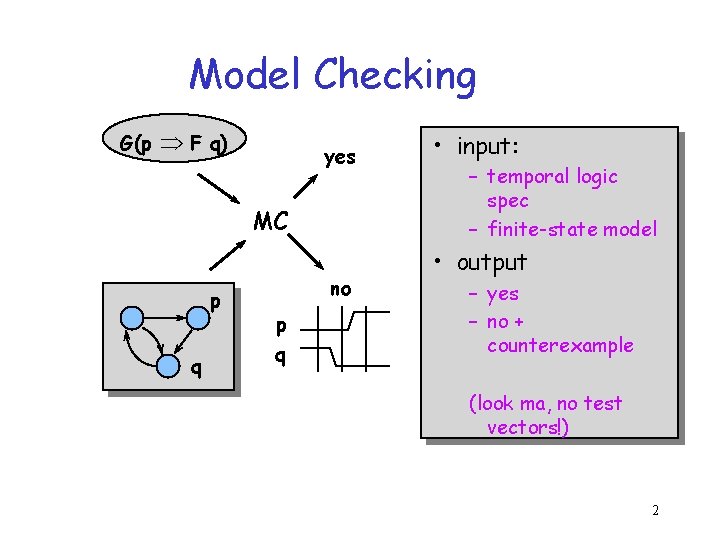
Model Checking G(p Þ F q) yes MC p q no p q • input: – temporal logic spec – finite-state model • output – yes – no + counterexample (look ma, no test vectors!) 2

Temporal logic (LTL) • A logical notation that allows to: – specify relations in time – conveniently express finite control properties • Temporal operators –Gp –Fp –Xp –p. Wq “henceforth p” “eventually p” “p at the next time” “p unless q” 5

Types of temporal properties • Safety (nothing bad happens) G ~(ack 1 & ack 2) “mutual exclusion” G (req Þ (req W ack)) “req must hold until ack” • Liveness (something good happens) G (req ÞF ack) “if req, eventually ack” • Fairness GF req Þ GF ack “if infinitely often req, infinitely often ack” 6

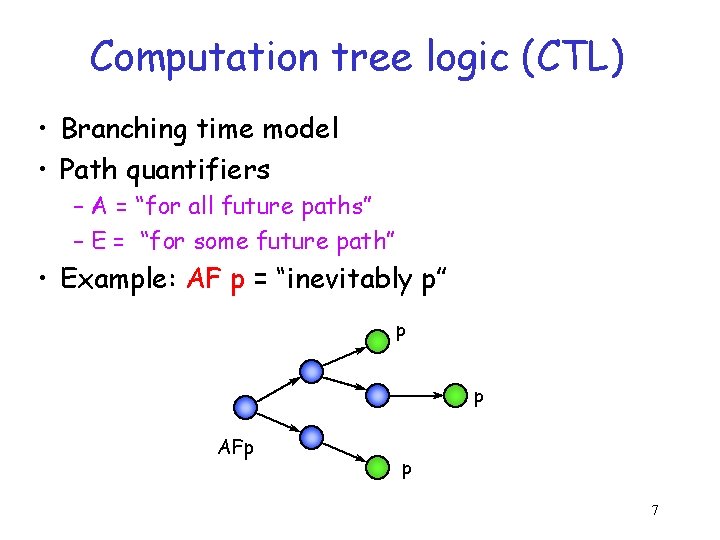
Computation tree logic (CTL) • Branching time model • Path quantifiers – A = “for all future paths” – E = “for some future path” • Example: AF p = “inevitably p” p p AFp p 7

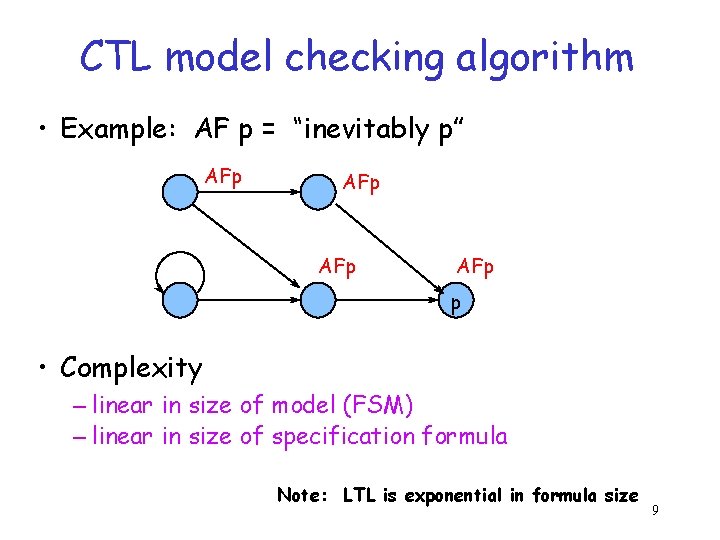
CTL model checking algorithm • Example: AF p = “inevitably p” AFp AFp p • Complexity – linear in size of model (FSM) – linear in size of specification formula Note: LTL is exponential in formula size 9

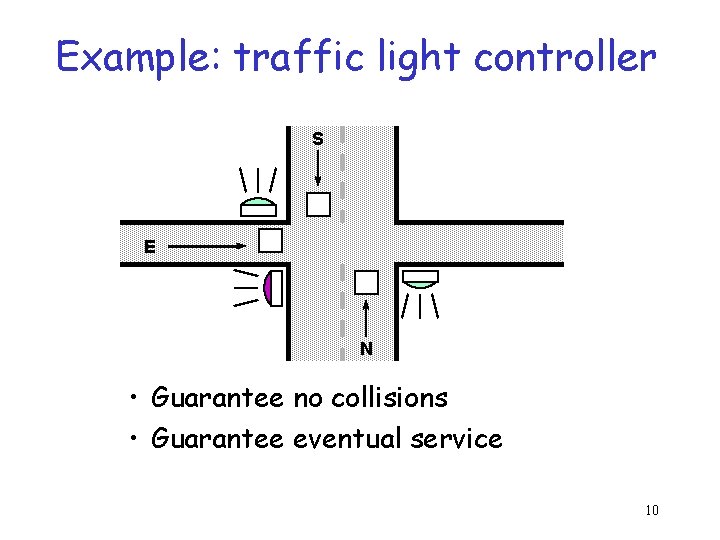
Example: traffic light controller S E N • Guarantee no collisions • Guarantee eventual service 10

Specifications • Safety (no collisions) AG Ø (E_Go Ù (N_Go | S_Go)); • Liveness AG (Ø N_Go Ù N_Sense Þ AF N_Go); AG (Ø S_Go Ù S_Sense Þ AF S_Go); AG (Ø E_Go Ù E_Sense Þ AF E_Go); • Fairness constraints infinitely often Ø(N_Go Ù N_Sense); infinitely often Ø(S_Go Ù S_Sense); infinitely often Ø(E_Go Ù E_Sense); (assume each sensor off infinitely often) 14

Counterexample • East and North lights on at same time. . . E_Go E_Req E_Sense NS_Lock N_Go N_Req N light goes on at same time S light goes off. S takes priority and resets NS_Lock N_Sense S_Go S_Req S_Sense 15

State explosion problem • What if the state space is too large? – too much parallelism – data in model • Approaches – Abstraction/reduction – “Symbolic” methods – Exploiting symmetry – “Partial order” methods 20

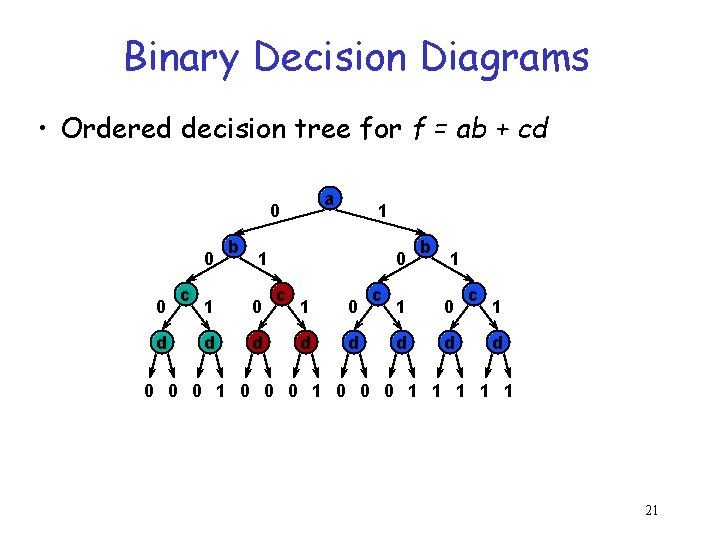
Binary Decision Diagrams • Ordered decision tree for f = ab + cd a 0 0 0 d c b 1 1 1 0 d d 0 c 1 0 d d c b 1 1 0 d d c 1 d 0 0 0 1 1 1 21

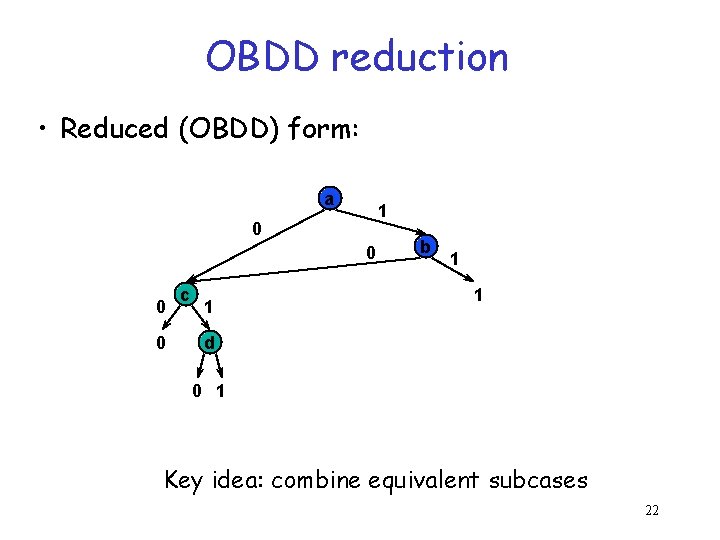
OBDD reduction • Reduced (OBDD) form: a 1 0 0 c 1 b 1 1 d 0 1 Key idea: combine equivalent subcases 22

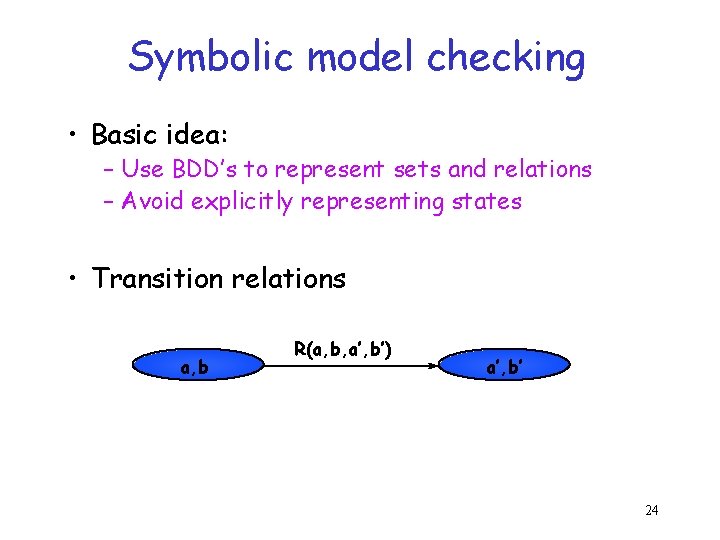
Symbolic model checking • Basic idea: – Use BDD’s to represent sets and relations – Avoid explicitly representing states • Transition relations a, b R(a, b, a’, b’) a’, b’ 24

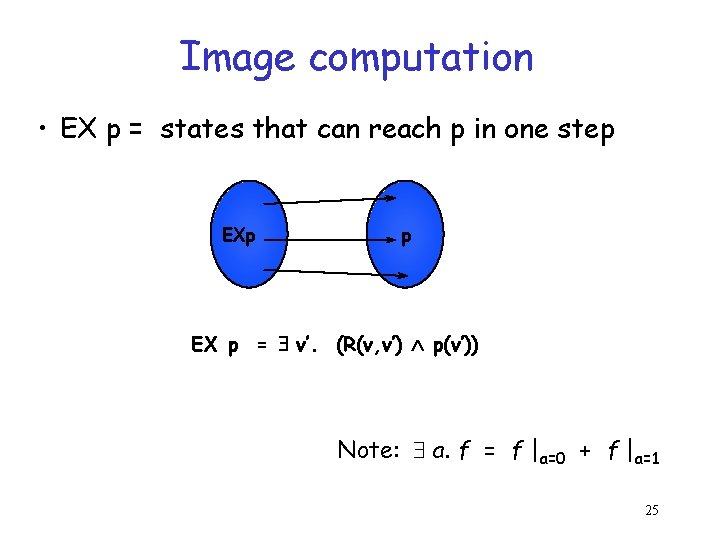
Image computation • EX p = states that can reach p in one step EXp p EX p = $ v’. (R(v, v’) Ù p(v’)) Note: $ a. f = f |a=0 + f |a=1 25

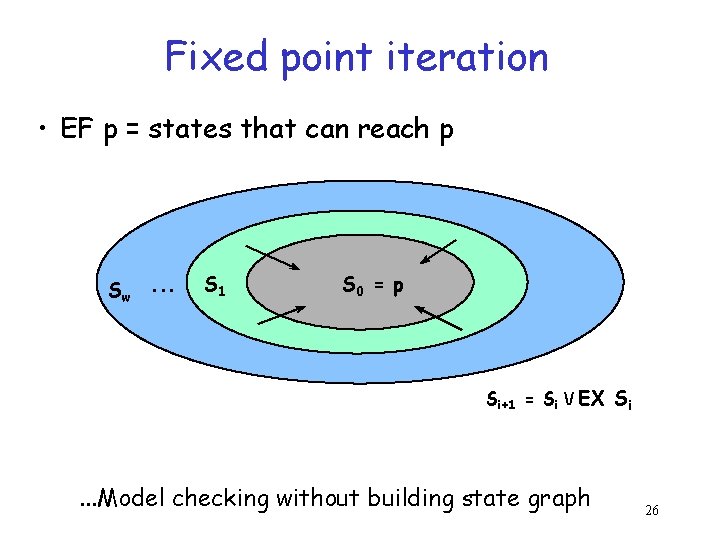
Fixed point iteration • EF p = states that can reach p Sw. . . S 1 S 0 = p Si+1 = Si / EX Si . . . Model checking without building state graph 26

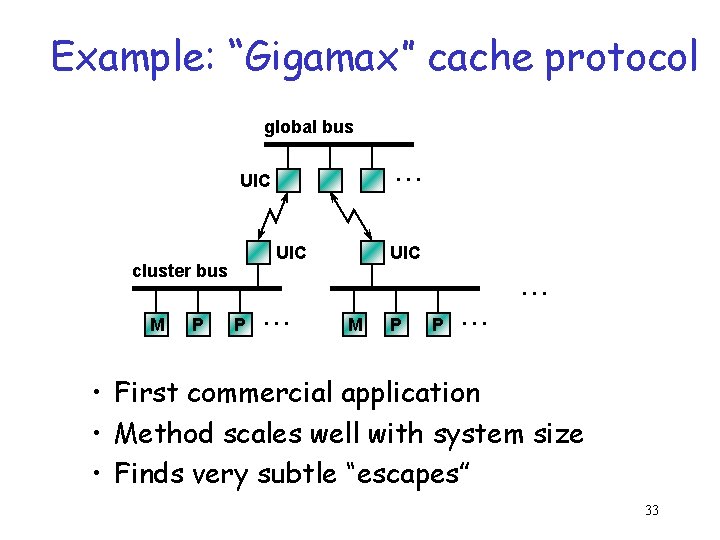
Example: “Gigamax” cache protocol global bus. . . UIC cluster bus M P UIC. . . P . . . M P P . . . • First commercial application • Method scales well with system size • Finds very subtle “escapes” 33

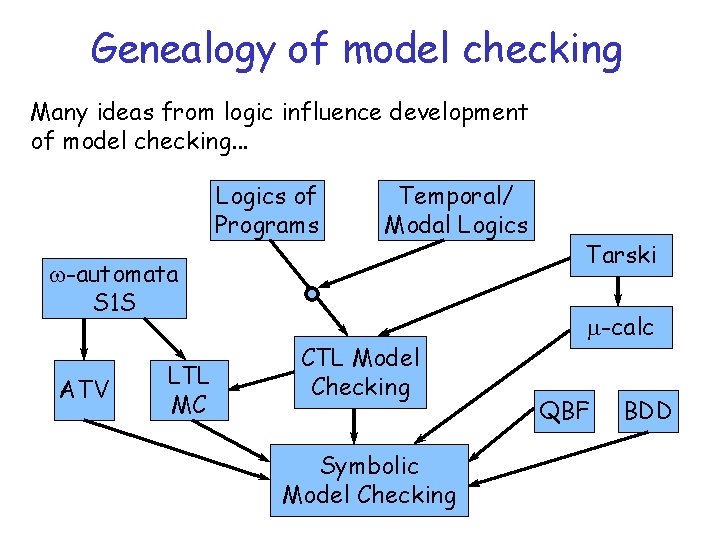
Genealogy of model checking Many ideas from logic influence development of model checking. . . Logics of Programs Temporal/ Modal Logics w-automata S 1 S ATV LTL MC CTL Model Checking Symbolic Model Checking Tarski m-calc QBF BDD

Logics of programs • Floyd/Hoare/Dijkstra – Give precise definitions of programming languages – Allows reasoning about programs (proofs/derivations) – Pre-post conditions/ weakest precondition • example: assignment axioms {true} x : =y {x = y} {P} x : = y {P} (no x in P)

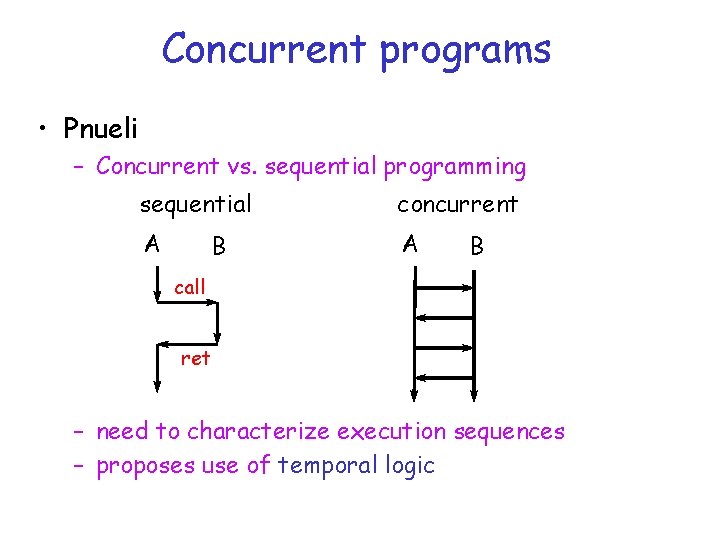
Concurrent programs • Pnueli – Concurrent vs. sequential programming sequential concurrent A A B B call ret – need to characterize execution sequences – proposes use of temporal logic

Temporal and modal logics • Roots in philosophical logic – Tense logic -- formalizing linguistic time “If a, then b before c” – Modal logic -- reasoning about possibility “If I had run I would have caught my plane” • New use in computer science: – characterize the interactions of parallel processes G req Þ F ack

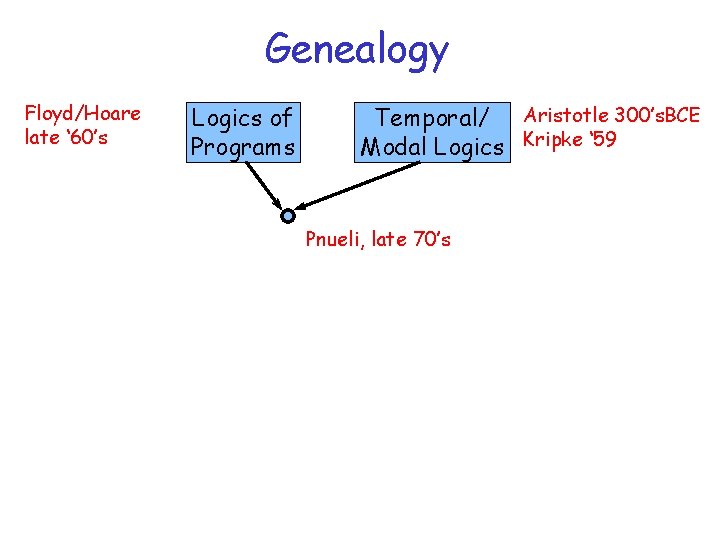
Genealogy Floyd/Hoare late ‘ 60’s Logics of Programs Temporal/ Aristotle 300’s. BCE Modal Logics Kripke ‘ 59 Pnueli, late 70’s

CTL Model checking • Reasoning about properties of nondeterministic programs – branching time properties of programs – fixed point characterizations (Tarski) • every monotonic function has least/greatest fixed point – key idea: apply to finite graphs, not infinite trees • can directly calculate Tarski fixed points • Applications – finite state machines in hardware – protocols – proved incorrectness of some published designs

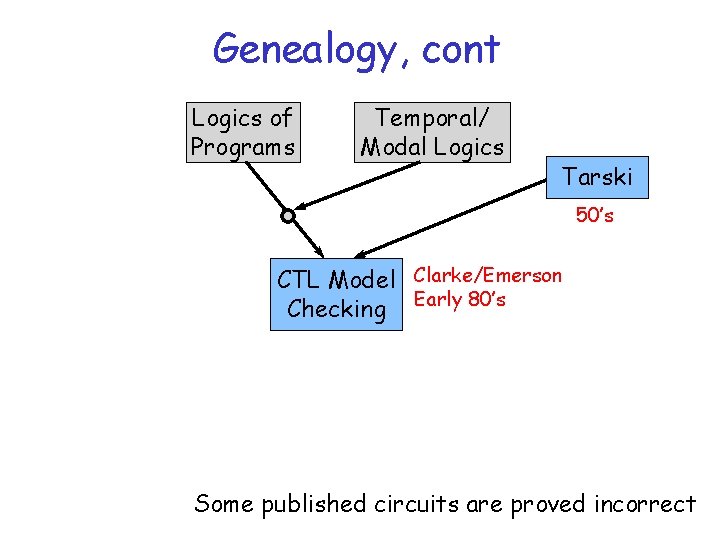
Genealogy, cont Logics of Programs Temporal/ Modal Logics Tarski 50’s CTL Model Clarke/Emerson Checking Early 80’s Some published circuits are proved incorrect

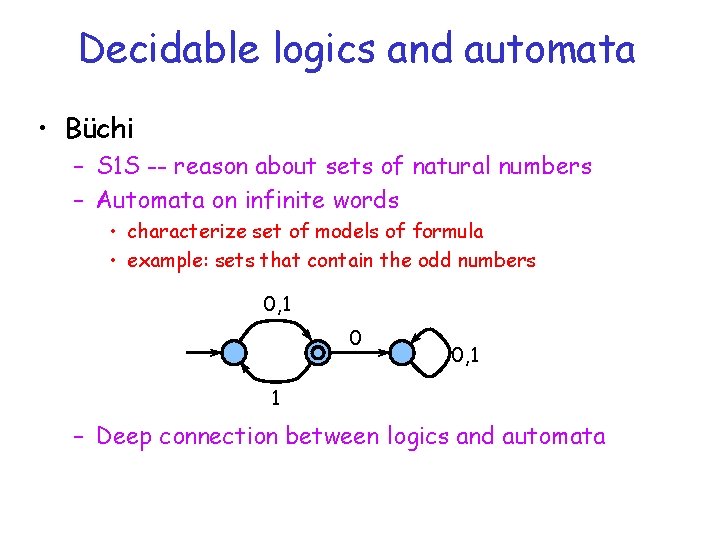
Decidable logics and automata • Büchi – S 1 S -- reason about sets of natural numbers – Automata on infinite words • characterize set of models of formula • example: sets that contain the odd numbers 0, 1 0 0, 1 1 – Deep connection between logics and automata

LTL model checking • Vardi and Wolper – Apply Büchi’s technique to LTL – Automaton construction yields optimal decision algorithm • Kurshan – Specify properties directly as automata • example: infinitely often p (GFp) p Øp true

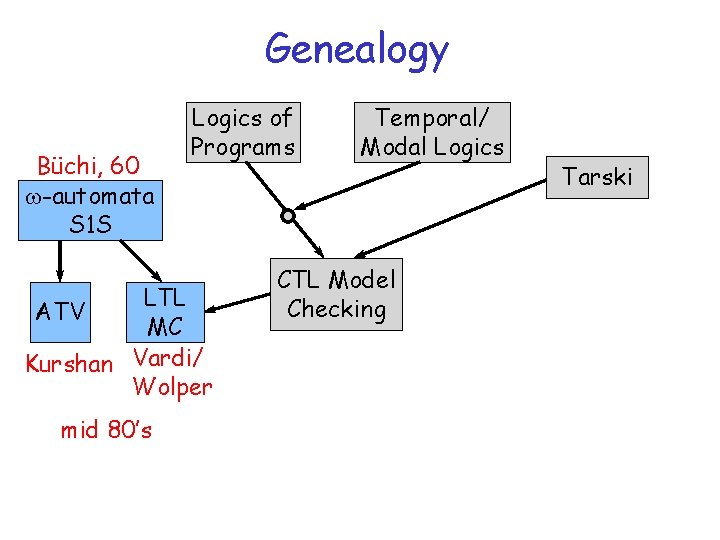
Genealogy Büchi, 60 w-automata S 1 S Logics of Programs LTL ATV MC Kurshan Vardi/ Wolper mid 80’s Temporal/ Modal Logics CTL Model Checking Tarski

Symbolic Model Checking • State explosion problem – graph model guarantees worst-case complexity • Characterize sets and relations by Boolean formulas – compute Tarski fixed points directly on formulas EXp = $v¢. (R Ù p¢) (QBF) – Use BDD’s to represent formulas • efficient canonical form

Mu-calculus • Park’s Mu-Calculus – Logic of relations with fixed point operator – Can express transitive closure – Nicely characterizes what SMC can compute • SMC algorithm for Mu-calculus – Use to express symbolic algorithms for • CTL, LTL model checking AFp = m. Q. p Ú AX Q • Automaton containment, etc. . . – Note: bad specification logic, but good for describing algorithms

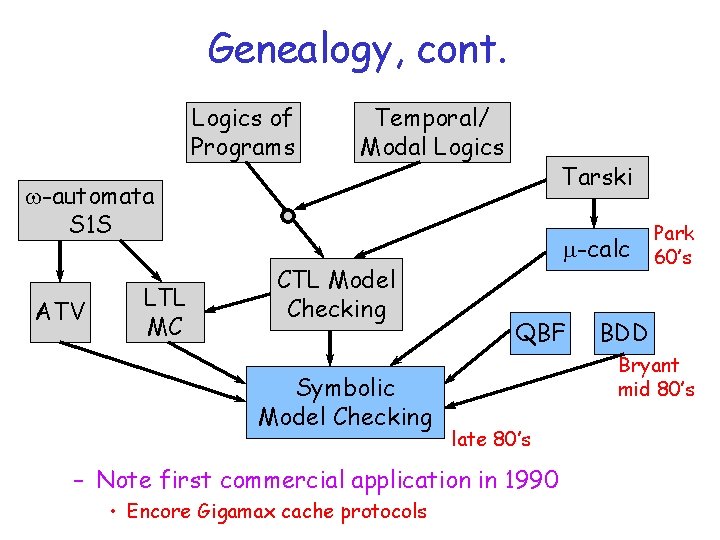
Genealogy, cont. Logics of Programs Temporal/ Modal Logics Tarski w-automata S 1 S ATV LTL MC CTL Model Checking Symbolic Model Checking m-calc QBF BDD Bryant mid 80’s late 80’s – Note first commercial application in 1990 • Encore Gigamax cache protocols Park 60’s

Applications • Hardware Design – Encore Gigamax – Intel instruction decoder – SGI cache protocol chip • Other areas – Avionics (TCAS) – Chemical plant control – Nuclear storage facilities (!) • Commercial tools – Cadence, IBM, Synopsys

A convergence of research areas in logic • Many areas of logic have shaped the discourse in model checking – – – Logics of programs Temporal/Modal logics Tarski fixed point theory Decidable logics -- S 1 S/automata Park’s mu-calculus • Much of this work is quite abstract, but has strongly influenced practical work in model checking