A Brief History of 3 D MESH COMPRESSION

A Brief History of 3 D MESH COMPRESSION ORAL, M. ELMAS, A. A. 1

Outline ■ 3 D Models and Polygonal Mesh Usage Areas ■ Polygonal Mesh Basics ■ Representation and Storage ■ Compression – Single Rate Mesh Compression ■ Geometry Compression ■ Connectivity Compression ■ Pioneering Algorithms ■ Performance Results ■ Conclusion ■ Algorithms – Geometry Compression – Topological Surgery – Edge. Breaker – Triangle Mesh Compression 2

Movies “Rustboy” animated short by Brian Taylor 3

Engineering “Audi A 8” created by Roland Wolf 4

Architectural Visualization “Atrium” created by Karol Myszkowski and Frederic Drago 5

Product Catalogues “Bedroom set-model Assisi” created by Stolid 6

Historical Study scanning of “Michelangelo’s David” courtesy of Marc Levoy 7

Computer Games screenshot of “The village of Gnisis”, The Elder Scrolls III 8

Polygonal Mesh & Mesh Basics 9

Polygonal Mesh & Mesh Basics Mesh with Holes Mesh with Handles Simple Mesh with Holes & Handles 10

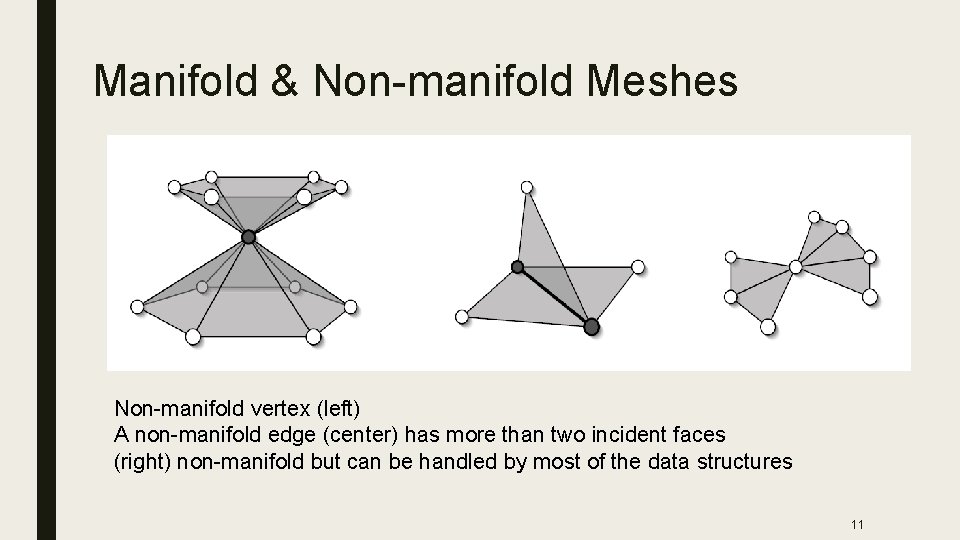
Manifold & Non-manifold Meshes Non-manifold vertex (left) A non-manifold edge (center) has more than two incident faces (right) non-manifold but can be handled by most of the data structures 11

3 D Polygonal Mesh Isenberg 12

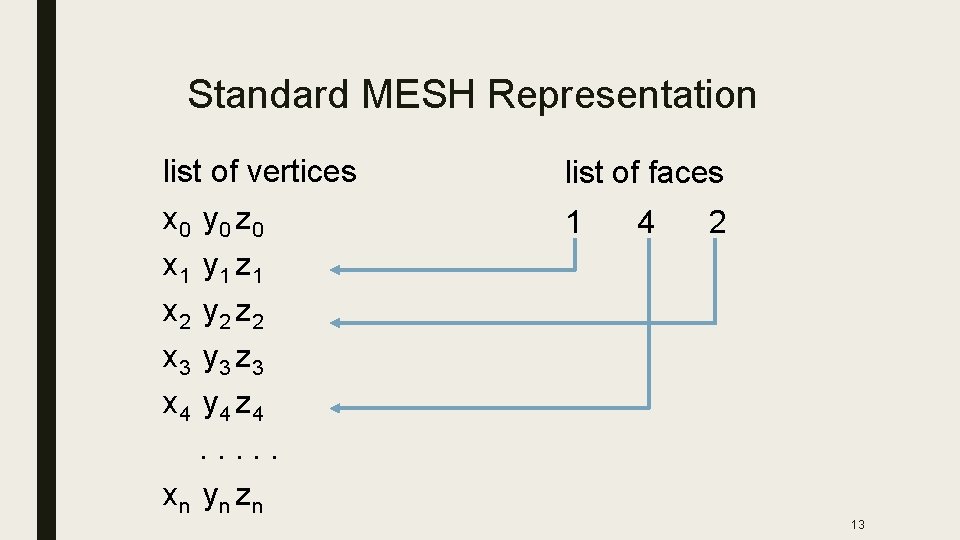
Standard MESH Representation list of vertices x 0 y 0 z 0 x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 x 4 y 4 z 4. . . xn yn zn list of faces 1 4 2 13

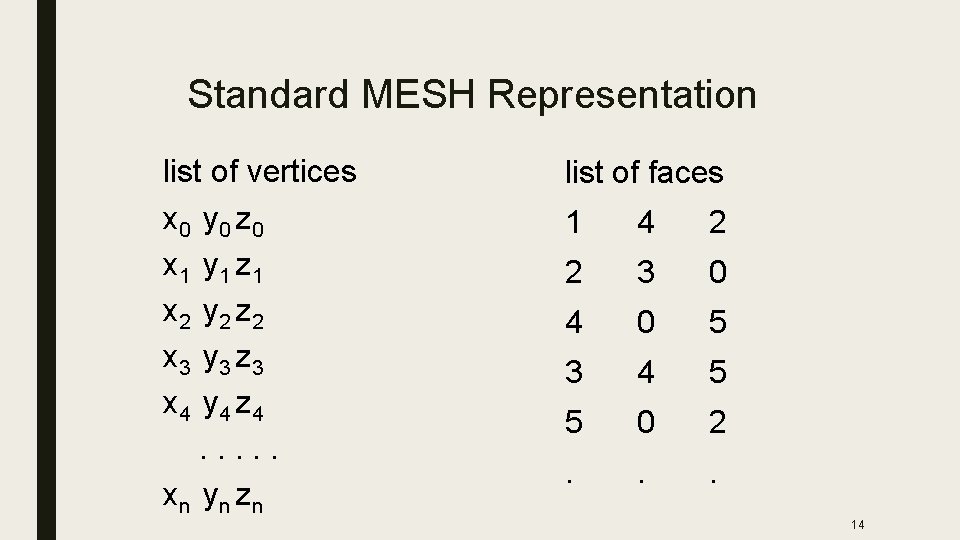
Standard MESH Representation list of vertices x 0 y 0 z 0 x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 x 4 y 4 z 4. . . xn yn zn list of faces 1 4 2 2 3 0 4 0 5 3 4 5 5 0 2 . . . 14

Geometry and Connectivity Information ■ Minimal information need to be stored is: – Where are the vertices located? => Mesh Geometry – How are the vertices connected? => Mesh Connectivity 15

Basic Ingredients for Mesh ■ Connectivity face 1 1 2 3 4 face 2 3 4 3 face 3 5 2 1 3. . facef 725 6291 6293 ■ Geometry vertex 1 ( x 1 vertex 2 ( x 2 vertex 3 ( x 3. . vertexv ( xv y 1 z 1 ) y 2 z 2 ) y 3 z 3 ) yv zv ) 16

Optional Ingredients for Mesh ■ Mapping face 1 1 2 face 2 3 4 face 3 5 6. . facef 9152 ■ Values texcoord 1 texcoord 2 texcoord 3. . texcoordt 3 4 5 1 7 123 271 (u 1 v 1) (u 2 v 2) (u 3 v 3) (ut vt) 17

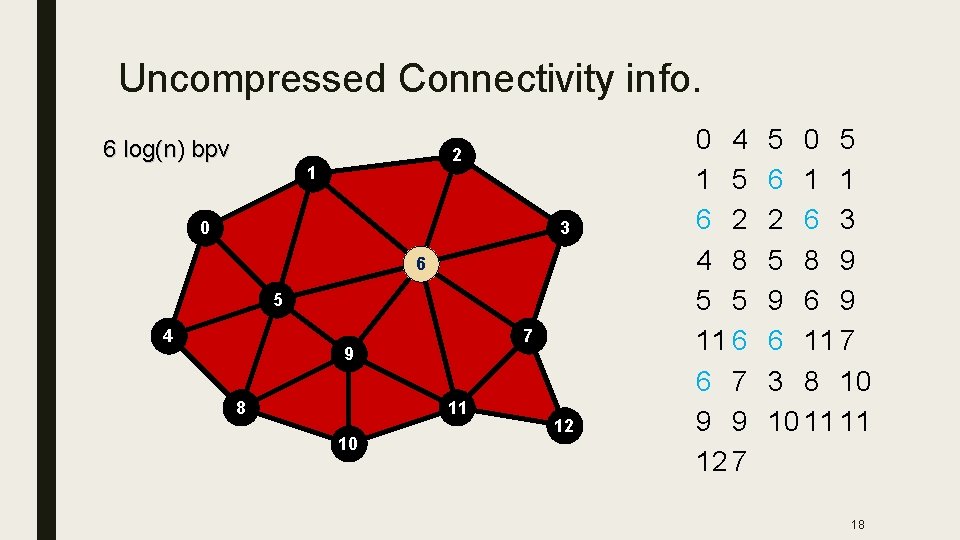
Uncompressed Connectivity info. 6 log(n) bpv 2 1 3 0 6 5 4 7 9 11 8 10 12 0 4 1 5 6 2 4 8 5 5 11 6 6 7 9 9 12 7 5 0 5 6 1 1 2 6 3 5 8 9 9 6 11 7 3 8 10 10 11 11 18

Pioneering Compression Algorithms ■ Geometry Compression (GC) Java 3 D ■ Geometry Compression Through Topological Surgery (TS) MPEG - 4 ■ Edgebreaker (EB) ■ Triangle Mesh Compression (TG 98) Virtue 3 D 19

Other triangle based connectivity driven single-rate mesh compression algorithms ■ Geometry Compression, [Deering, 95] ■ Topological Surgery, [Taubin & Rossignac, 98] ■ Cut-Border Machine, [Gumhold & Strasser, 98] ■ Triangle Mesh Compression, [Touma & Gotsman, 98] ■ Edgebreaker, [Rossignac, 99] ■ Spectral Compression of Geometry, [Karni & Gotsman, 00] ■ Face Fixer, [Isenburg & Snoeyink, 00] ■ Valence-driven Connectivity Coding, [Alliez & Desbrun, 01] ■ Near-Optimal Coding, [Khodakovsky, Alliez, Desbrun & ■ Degree Duality Coder, [Isenburg, 02] ■ Polygonal Parallelogram Prediction, [Isenburg & Alliez, 02] 20

Geometry Compression Deering ‘ 95 1. Convert triangle data to generalized triangle mesh 2. Quantization of positions, colors, normals 3. Delta encoding of quantized values 4. Huffman tag-based variable-length encoding of deltas 5. Output binary output stream with Huffman table initializations and geometry compression instructions 21

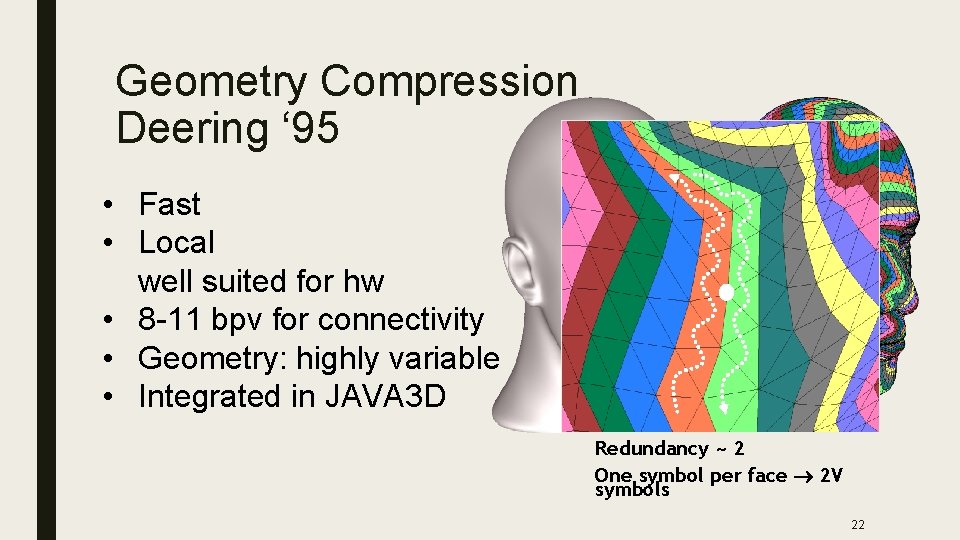
Geometry Compression Deering ‘ 95 • Fast • Local well suited for hw • 8 -11 bpv for connectivity • Geometry: highly variable • Integrated in JAVA 3 D Redundancy ~ 2 One symbol per face 2 V symbols 22

Topological Surgery • The idea is to cut a given mesh along a selected set of edges to make a planar mesh. The mesh connectivity is then represented by these cuts and planar mesh. • TS encodes a triangular mesh with about 2. 5 to 6 b/v • Spanning trees: a vertex and a triangle spanning tree • Connectivity encoding is lossless. • Geometry is predictively encoded. • The correction vectors are entropy encoded. • Normals, and colors are quantized. • Obtaining the optimal spanning tree is an NP-hard combinatorial problem. 23

Edge. Breaker ■ Lossless compression for a triangle mesh, using ≈2 bits per triangle for simple meshes. Only a slight increase for meshes with holes and handles. ■ Destroy triangles of the mesh one-by-one, starting from the boundary and spiraling inwards ■ For each destruction operation, store an opcode indicating the type of the operation – Sequence of opcodes is called “history” – Length of history = number of triangles, hence linear size encoding ■ Compression scheme: remove X, store the operation (C, L, E, R or S), update the bounding loop and advance the gate 24

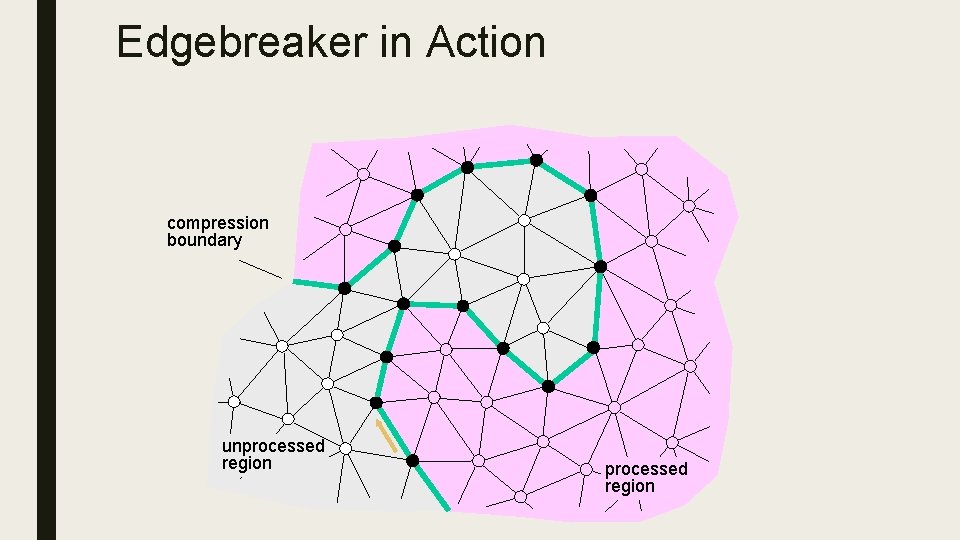
Edgebreaker in Action 5 compression boundary unprocessed region

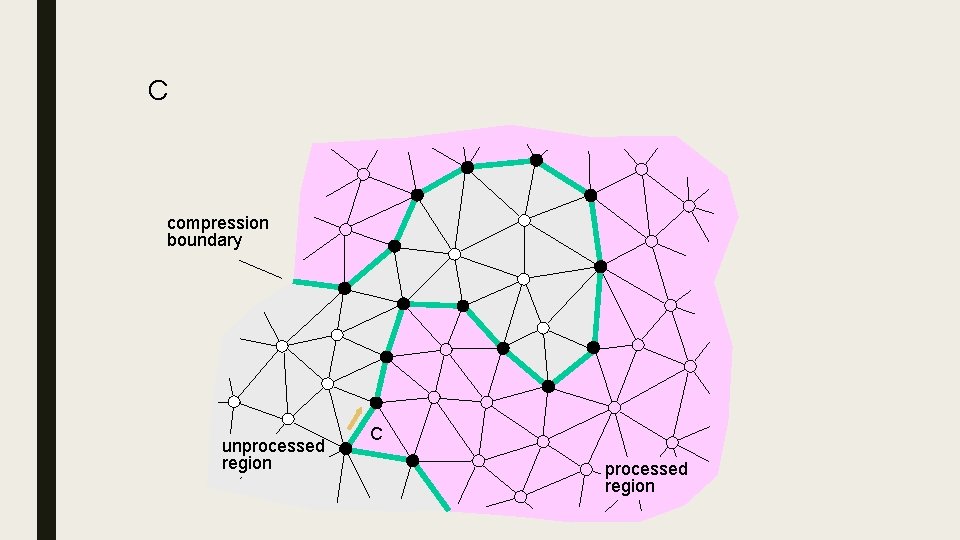
C 5 compression boundary unprocessed region C processed region

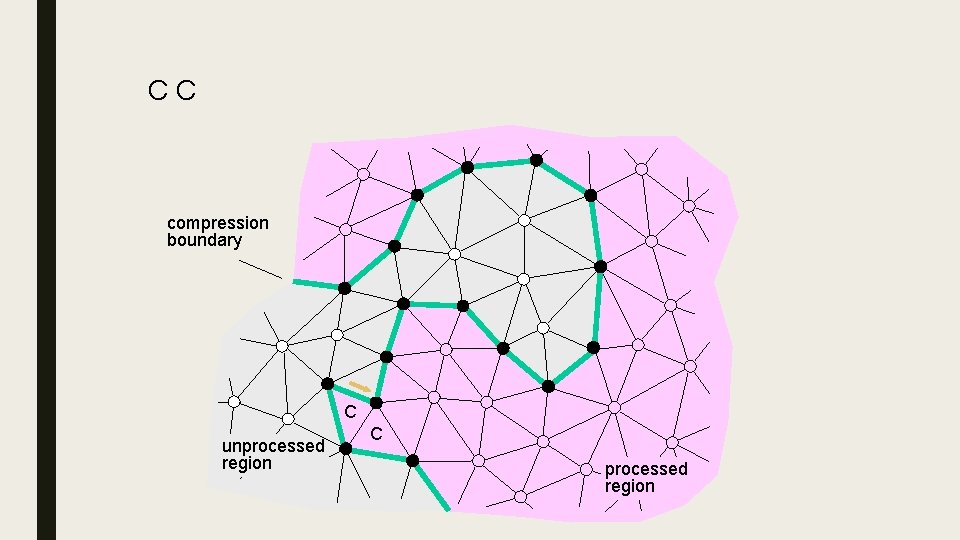
CC 5 compression boundary C unprocessed region C processed region

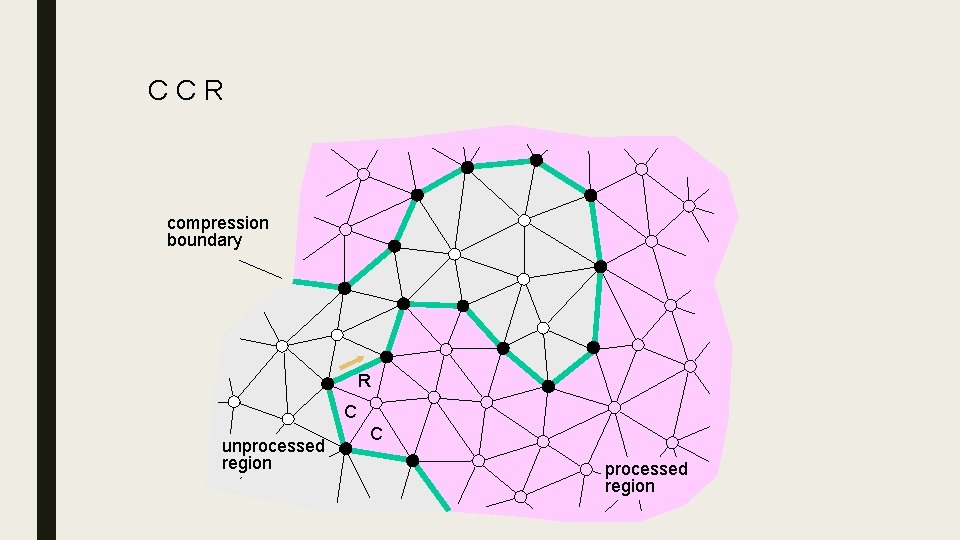
CCR 5 compression boundary R C unprocessed region C processed region

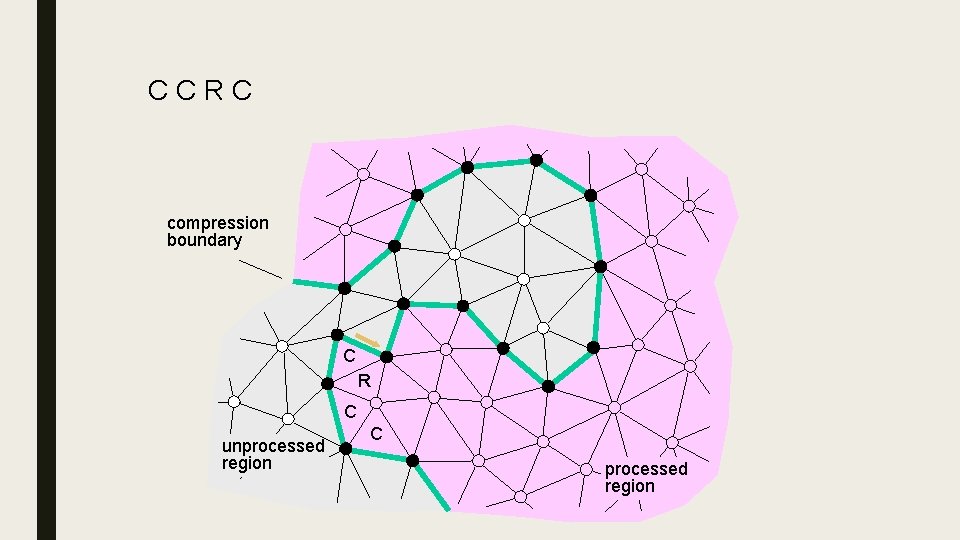
CCRC 5 compression boundary C R C unprocessed region C processed region

CCRCR 5 compression boundary R C unprocessed region C processed region

CCRCRS offset = 11 8 7 10 compression boundary 11 1 S R C R 5 9 6 2 3 5 4 C unprocessed region C processed region

CCRCRSL offset = 11 5 compression boundary L S R C unprocessed region C processed region

CCRCRSLC offset = 11 5 compression boundary L C S R C unprocessed region C processed region

CCRCRSLCR offset = 11 5 compression boundary L C R S R C unprocessed region C processed region

CCRCRSLCRC offset = 11 5 compression boundary L C R C S R C unprocessed region C processed region

CCRCRSLCRCR offset = 11 5 compression boundary L S C R R C unprocessed region C processed region

CCRCRSLCRCRC offset = 11 5 compression boundary L S C R R C C R C unprocessed region C processed region

CCRCRSLCRCRCR offset = 11 5 compression boundary L S C R R C R C unprocessed region C processed region

CCRCRSLCRCRCRR offset = 11 5 compression boundary L S C R C R R C unprocessed region C processed region

CCRCRSLCRCRCRRR offset = 11 5 compression boundary L S C R R R C unprocessed region C processed region

CCRCRSLCRCRCRRRL offset = 11 5 compression boundary L S C R R L R C R R C unprocessed region C processed region

CCRCRSLCRCRCRRRLC offset = 11 5 compression boundary L S C C R R L R C R R C unprocessed region C processed region

CCRCRSLCRCRCRRRLCR offset = 11 5 compression boundary R L S C C R R L R C R R C unprocessed region C processed region

CCRCRSLCRCRCRRRLCRR offset = 11 R 5 compression boundary R L S C C R R L R C R R C unprocessed region C processed region

CCRCRSLCRCRCRRRLCRRR offset = 11 R R 5 compression boundary R L S C C R R L R C R R C unprocessed region C processed region

offset = 3 CCRCRSLCRCRCRRRLCRRRS offset = 11 R compression boundary S R 2 L S C C R R L R C 5 1 R R R C unprocessed region C processed region

offset = 3 CCRCRSLCRCRCRRRLCRRRSR offset = 11 R compression boundary L S C S R C R R R L R C 5 R R R C unprocessed region C processed region

offset = 3 CCRCRSLCRCRCRRRLCRRRSRE offset = 11 R compression boundary E L S C S R C R R R L R C 5 R R R C unprocessed region C processed region

offset = 3 CCRCRSLCRCRCRRRLCRRRSREE offset = 11 R compression boundary E L S C S R E R C C R R R L R C 5 R R R C unprocessed region C processed region

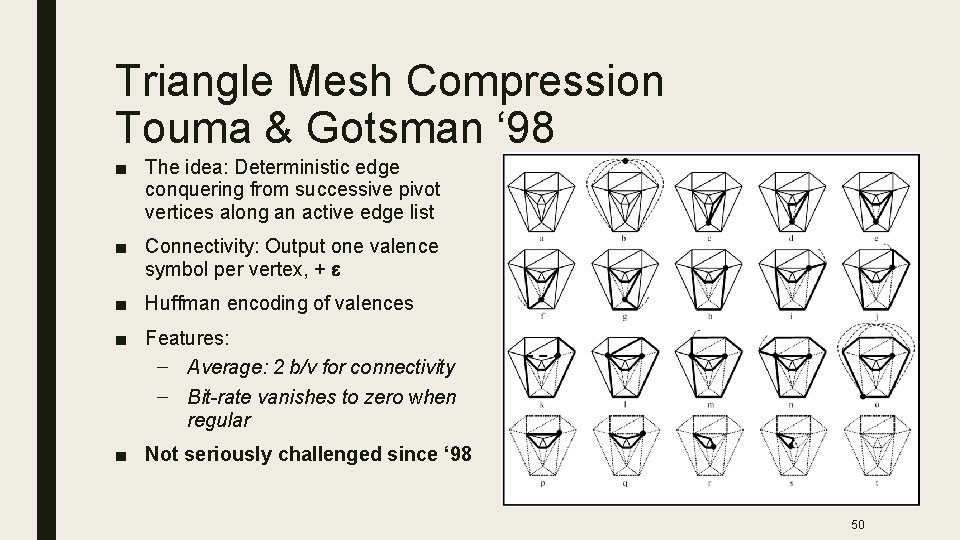
Triangle Mesh Compression Touma & Gotsman ‘ 98 ■ The idea: Deterministic edge conquering from successive pivot vertices along an active edge list ■ Connectivity: Output one valence symbol per vertex, + ■ Huffman encoding of valences ■ Features: – Average: 2 b/v for connectivity – Bit-rate vanishes to zero when regular ■ Not seriously challenged since ‘ 98 50

TG coder slot counts 5 compression boundary unprocessed region

TG coder 7 5 compression boundary unprocessed 7 region processed region

TG coder 6 5 7 compression boundary zero slot 6 unprocessed 7 region processed region

TG coder 6 5 7 compression boundary 6 unprocessed 7 region processed region

TG coder 6 5 5 7 compression boundary zero slot 5 6 unprocessed 7 region processed region

TG coder 6 5 5 7 compression boundary 5 6 unprocessed 7 region processed region

TG coder 7 6 5 S offset = 18 15 12 5 16 13 compression boundary 18 S 5 11 2 4 6 8 7 6 unprocessed 7 region processed region

TG coder 7 6 5 S offset = 18 5 compression boundary S 5 6 unprocessed 7 region processed region

TG coder 7 6 5 S 7 offset = 18 5 compression boundary 7 S 5 6 unprocessed 7 region processed region

TG coder 7 6 5 S 7 offset = 18 compression boundary 5 zero slot 7 S 5 6 unprocessed 7 region processed region

TG coder 7 6 5 S 7 offset = 18 5 zero slot compression boundary 7 S 5 6 unprocessed 7 region processed region

TG coder 7 6 5 S 7 offset = 18 5 compression boundary 7 S 5 6 unprocessed 7 region processed region

TG coder 7 6 5 S 7 6 offset = 18 5 compression boundary 7 S 6 5 6 unprocessed 7 region processed region

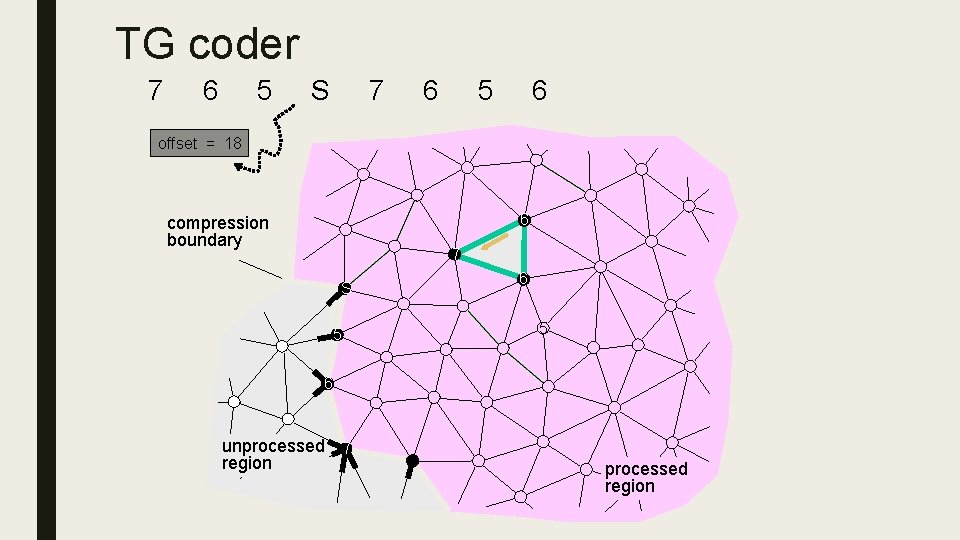
TG coder 7 6 5 S 7 6 5 offset = 18 5 compression boundary 7 S 5 6 unprocessed 7 region processed region

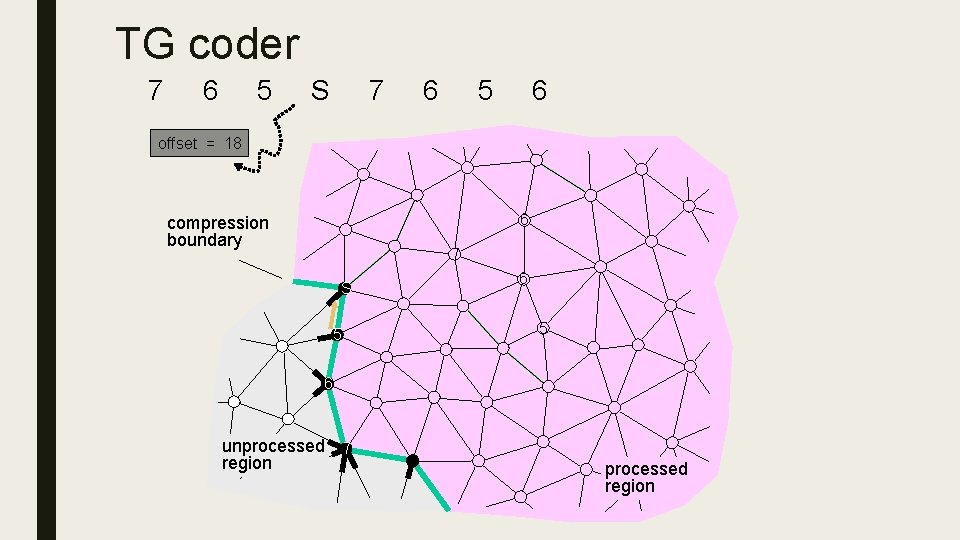
TG coder 7 6 5 S 7 6 5 6 offset = 18 5 6 compression boundary 7 S 5 6 unprocessed 7 region processed region

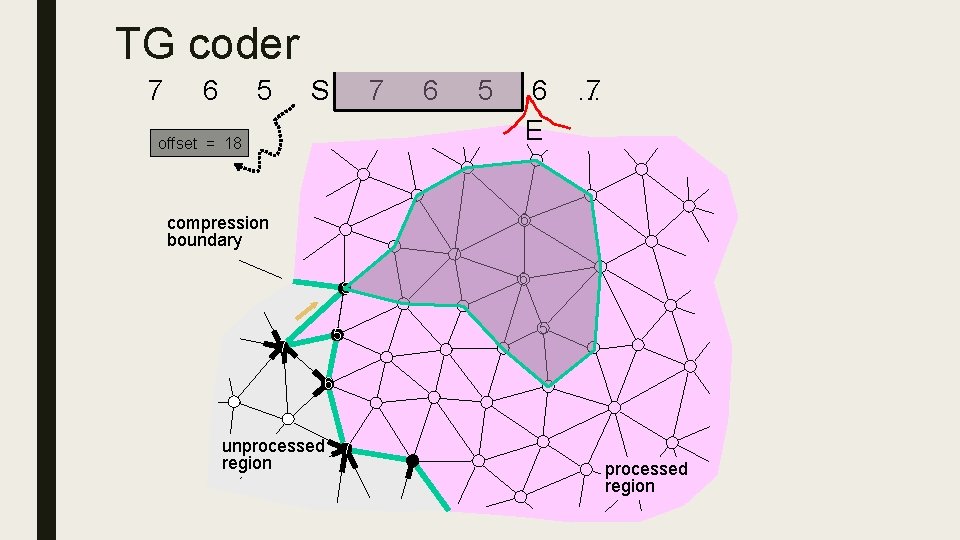
TG coder 7 6 5 S 7 6 5 offset = 18 6 E 7 … 5 6 compression boundary 7 S 5 7 6 5 6 unprocessed 7 region processed region

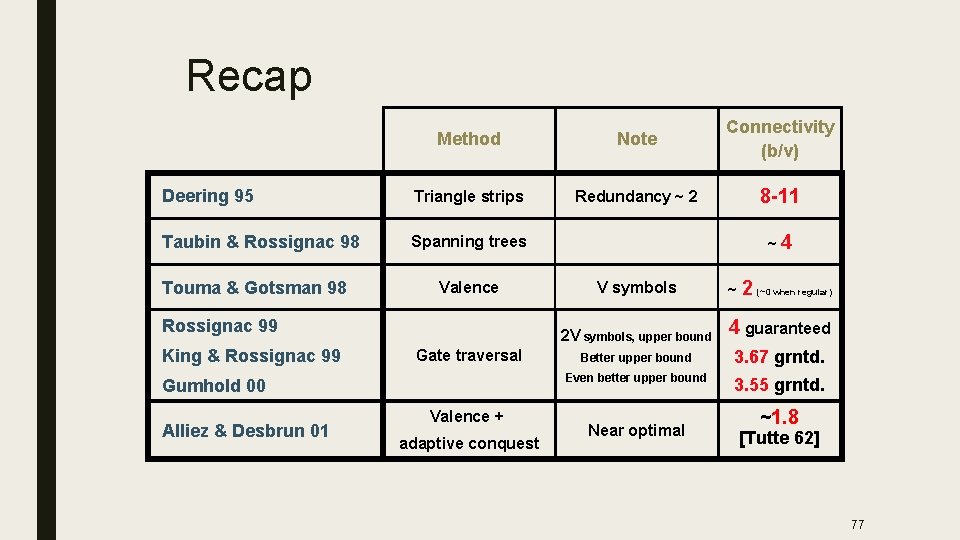
Recap Method Note Connectivity (b/v) Deering 95 Triangle strips Redundancy ~ 2 8 -11 Taubin & Rossignac 98 Spanning trees Touma & Gotsman 98 Valence Rossignac 99 King & Rossignac 99 Gate traversal Gumhold 00 Alliez & Desbrun 01 Valence + adaptive conquest ~4 V symbols ~ 2 (~0 when regular) 2 V symbols, upper bound 4 guaranteed Better upper bound 3. 67 grntd. Even better upper bound 3. 55 grntd. Near optimal ~1. 8 [Tutte 62] 77

Conclusions The valence approach guarantees: Optimality in the regular case (6. . 6) *Near* optimality in the irregular case