A Boosting Algorithm for Classification of SemiStructured Text

A Boosting Algorithm for Classification of Semi-Structured Text Taku Kudo * # Yuji Matsumoto * * Nara Institute Science and Technology # Currently, NTT Communication Science Labs. 1

Backgrounds n Text Classification using Machine Learning categories: topics (sports, finance, politics…) ¨ features: bag-of-words (BOW) ¨ methods: SVM, Boosting, Naïve Bayes ¨ n Changes in categories ¨ n modalities, subjectivities, or sentiments Changes in text size ¨ document (large) → passage, sentence (small) Our Claim: BOW is not sufficient 2

Backgrounds, cont. n Straightforward extensions ¨ n Add some structural features, e. g. , fixed-length N-gram or fixed-length syntactic relations But… Ad-hoc and task dependent ¨ require careful feature selections ¨ How to determine the optimal size (length) ? ¨ Use of larger substructures yields an inefficiency n Use of smaller substructures is the same as BOW n 3

Our approach n Semi-structured text ¨ assume that text is represented in a tree ¨ word sequence, dependency tree, base-phrases, XML n n Propose a new ML algorithm that can automatically capture relevant substructures in a semi-structured text Characteristics: ¨ Instance is not a numerical vector but a tree ¨ Use all subtrees as features without any constraints ¨ A compact and relevant feature set is automatically selected 4

Classifier for Trees 5

Tree classification problem n Goal: ¨ n Induce a mapping given training data from Training data ¨ A set of pairs of tree x and class label y (+1 or -1) +1 T= c a d -1 a , c d a +1 , a c d -1 b , c b d a 6

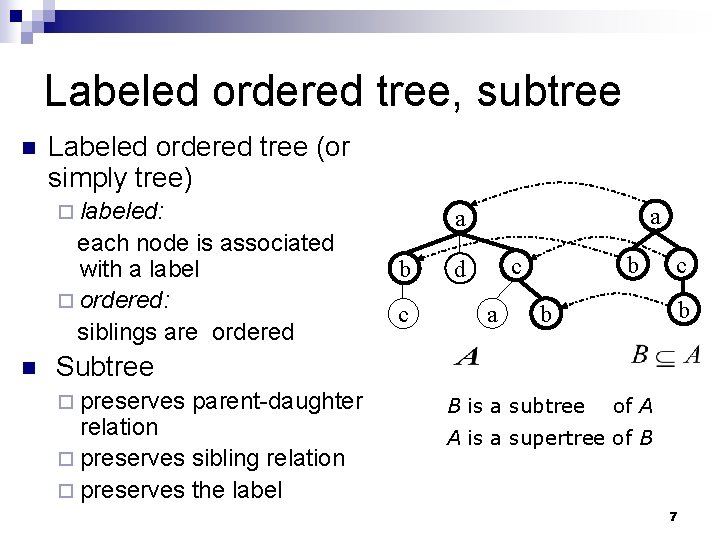
Labeled ordered tree, subtree n Labeled ordered tree (or simply tree) ¨ labeled: each node is associated with a label ¨ ordered: siblings are ordered n a a b c d a c b b Subtree ¨ preserves parent-daughter relation ¨ preserves sibling relation ¨ preserves the label B is a subtree of A A is a supertree of B 7

Decision stumps for trees n n A simple rule-based classifier <t, y> is a parameter (rule) of decision stumps x = c a d b c <t 1, y>=< a , +1> h (x) = 1 <t 1, y> d <t 2, y>=< b , -1> h (x) = 1 <t 2, y> 8

Decision stumps for trees, cont. n Training: select the optimal rule that maximizes the gain (or accuracy) n F: feature set (a set of all subtrees) 9

Decision stumps for trees, cont. +1 c <t, y> a, +1 a, -1 b, +1 a d a -1 d a +1 c a b +1 -1 -1 +1 +1 -1 -1 b d a c +1 -1 +1 gain 0 0 -1 … c d d c +1 a +1 -1 4 … d b c a -1 Select the optimal rule +1 +1 -1 +1 that yields the maximum gain 2 10

Boosting n n Decision stumps are too weak Boosting [Schapire 97] 1. 2. 3. 4. n build an weak leaner (decision stumps) Hj re-weight instances with respect to error rates repeat 1 to 2 in K times output a liner combination of H 1 ~ HK Redefine the gain to use Boosting 11

Efficient Computation 12

How to find the optimal rule? p F is too huge to be enumerated explicitly p Need to find the optimal rule efficiently A variant of Branch-and-Bound Define a search space in which whole set of subtrees is given n Find the optimal rule by traversing this search space n Prune the search space by proposing a criterion n 13

Right most extension [Asai 02, Zaki 02] n extend a given tree of size (n-1) by adding a new node to obtain trees of size n ¨a node is added to the right-most-path ¨ a node is added as the rightmost sibling 1 a 1 t a rightmost- path 2 b 4 3 c a 5 2 b 3 c 4 5 c 6 1 b 2 b 3 c a c 6 7 b 1 a 4 5 a c 6 b 7 2 b 3 c a 4 5 a c 6 7 b 14

Right most extension, cont. n Recursive applications of right most extensions create a search space 15

Pruning For all , propose an upper bound such that n Can prune the node t if , where is a suboptimal gain n Pruning strategy μ(t )=0. 4 implies the gain of any supertree of t is no grater than 0. 4 16

Upper bound of the gain (an extension of [Morishita 02]) 17

Relation to SVMs with Tree Kernel 18

Classification algorithm Modeled as a linear classifier wt : weight of tree t -b : bias (default class label) 19

SVMs and Tree Kernel [Collins 02] Tree Kernel: all subtrees are expanded implicitly a {0, …, 1, …, 1, …, 0, …} b c p Feature spaces are essentially the same p Learning strategies different a b are c a a a b c SVM: Boosting: 20

SVM v. s Boosting [Rätsch 01] n n Both are known as Large Margin Classifiers Metric of margin is different SVM: L 2 -norm margin - w is expressed in a small number of examples - support vectors - sparse solution in the example space Boosting: L 1 -norm margin - w is expressed in a small number of features - sparse solution in the feature space 21

SVM v. s Boosting, cont. n Accuracy is task-dependent n Practical advantages of Boosting: ¨ Good interpretability Can analyze how the model performs or what kinds of features are useful n Compact features (rules) are easy to deal with n ¨ Fast classification Complexity depends on the small number of rules n Kernel methods are too heavy n 22

Experiments 23

Sentence classifications n PHS: cell phone review classification (5, 741 sent. ) ¨ domain: Web-based BBS on PHS, a sort of cell phone ¨ categories: positive review or negative review positive: It is useful that we can know the date and time of E-Mails. negative: I feel that the response is not so good. n MOD: modality identification (1, 710 sent. ) ¨ domain : editorial news articles ¨ categories: assertion, opinion, or description assertion: We should not hold an optimistic view of the success of POKEMON. opinion: I think that now is the best time for developing the blue print. description: Social function of education has been changing. 24

Sentence representations n N-gram tree ¨ each word simply modifies the next word ¨ subtree is an N-gram (N is unrestricted) response is very good n dependency tree ¨ word-based dependency tree ¨ A Japanese dependency parser, Cabo. Cha, is used response is very good n bag-of-words (baseline) 25

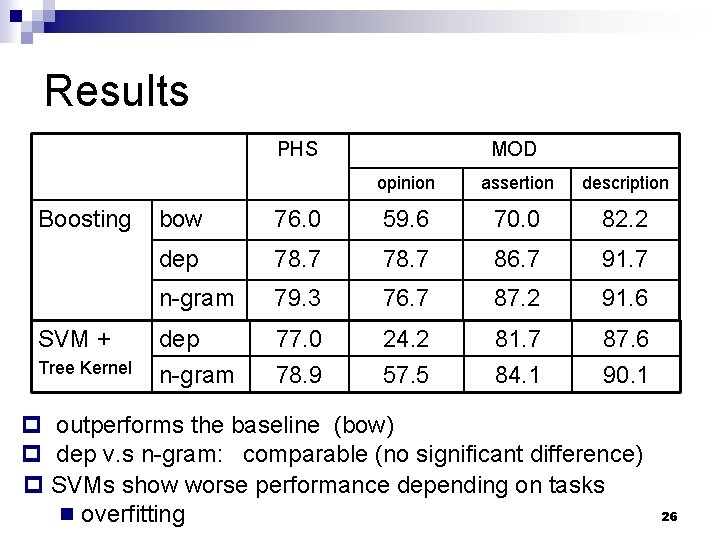
Results PHS Boosting SVM + Tree Kernel MOD opinion assertion description bow 76. 0 59. 6 70. 0 82. 2 dep 78. 7 86. 7 91. 7 n-gram 79. 3 76. 7 87. 2 91. 6 dep n-gram 77. 0 78. 9 24. 2 57. 5 81. 7 84. 1 87. 6 90. 1 p outperforms the baseline (bow) p dep v. s n-gram: comparable (no significant difference) p SVMs show worse performance depending on tasks n overfitting 26

Interpretability PHS dataset with dependency A: subtrees that include “hard, difficult ” 0. 0004 -0. 0006 -0. 0007 -0. 0017 be hard to hung up be hard to read be hard to use be hard to … C: subtrees that include “recharge” 0. 0028 recharging time is short -0. 0041 recharging time is long B: subtrees that include “use” 0. 0027 want to use 0. 0002 be in use 0. 0001 be easy to use -0. 0001 was easy to use -0. 0007 be hard to use -0. 0019 is easier to use than. . 27

Interpretability, cont. PHS dataset with dependency Input: The LCD is large, beautiful and easy to see weight w 0. 00368 0. 00353 0. 00237 0. 00174 0. 00107 0. 00074 0. 00057 0. 00036 -0. 00001 subtree t be easy to beautiful be easy to see is large The LCD is … The LCD see large 28

Advantages n Compact feature set ¨ Boosting extracts only 1, 783 unique features n ¨ n The set sizes of distinct 1 -gram, 2 -gram, and 3 -gram are 4, 211, 24, 206, and 43, 658 respectively SVMs implicitly use a huge number of features Fast classification ¨ Boosting: 0. 531 sec. / 5, 741 instances ¨ SVM: 255. 42 sec. / 5, 741 instances ¨ Boosting is about 480 times faster than SVMs 29

Conclusions n n Assume that text is represented in a tree Extension of decision stumps ¨ n n Boosting Branch and bound ¨ n all subtrees are potentially used as features enables to find the optimal rule efficiently Advantages: good interpretability ¨ fast classification ¨ comparable accuracy to SVMs with kernels 30 ¨

Future work n Other applications Information extraction ¨ semantic-role labeling ¨ parse tree re-ranking ¨ n Confidence rated predictions for decision stumps 31

Thank you! n An implementation of our method is available as an open source software at: http: //chasen. naist. jp/~taku/software/bact/ 32