A Boolean Paradigm in Multi Valued Logic Synthesis

A Boolean Paradigm in Multi. Valued Logic Synthesis Alan Mishchenko Electrical and Computer Engineering Portland State University Robert K. Brayton Electrical Engineering and Computer Science University of California, Berkeley June 5, 2002 IWLS 2002, New Orleans, Louisiana

Overview • Motivation • Background • Optimization Algorithms – – – Node simplification Partial encoding Decomposition Resubstitution Common logic extraction • Case study: Decomposition and SAT • Conclusions 9/16/2020 IWLS 2002, New Orleans, Louisiana 2

Algebraic vs. Boolean Algorithms • Most of the currently used logic synthesis algorithms are algebraic (do not use Boolean identities such as a a = a and a a’ = 0) – sub-optimal quality, fast • Boolean algorithms are also known but seldom used – better quality, slower • There is no unified picture of the Boolean algorithms for logic synthesis 9/16/2020 IWLS 2002, New Orleans, Louisiana 3

Goals of the Present Work • Develop Boolean algorithms working on MV relations • Explore interdependence and common computational core of the Boolean algorithms • This study is possible because of the vantage point of multi-valued logic optimization 9/16/2020 IWLS 2002, New Orleans, Louisiana 4

Optimization Algorithms • Node simplification • Partial (value reducing) encoding • Decomposition • Resubstitution • Common logic extraction 9/16/2020 IWLS 2002, New Orleans, Louisiana 5

Node Simplification Compute and use complete flexibility (CF) to simplify the node: 1. CF in global space: R(X, yi) = Z [ R(X, yi, Z) R(X, Z) ] 2. CF in local space: R(Y, yi) = X [ M(X, Y) R(X, yi) ] 3. Use R(Y, yi) to optimize MV-SOP (heuristic, exact) 9/16/2020 IWLS 2002, New Orleans, Louisiana 6

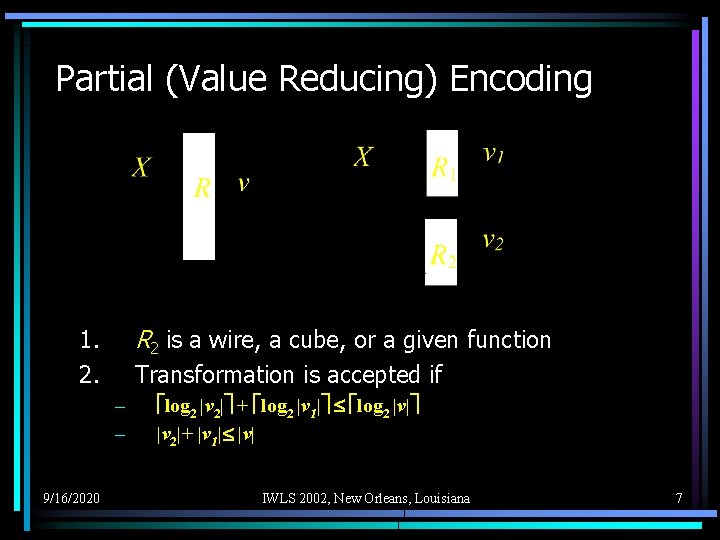
Partial (Value Reducing) Encoding R 2 is a wire, a cube, or a given function Transformation is accepted if 1. 2. – – 9/16/2020 log 2 |v 2| + log 2 |v 1| log 2 |v| |v 2|+ |v 1| |v| IWLS 2002, New Orleans, Louisiana 7

Decomposition and Encoding 1. 2. 3. 4. 9/16/2020 Select bound set XB Compute the CF of block B 1 assuming v 1 is the product of values in XB (column compatibility is not used) Encode B 1 using value-reducing encoding to get B 2 Inputs in XC are shared, which leads to non-disjoint decomposition IWLS 2002, New Orleans, Louisiana 8

Resubstitution 1. Compute R(Y, y), the complete flexibility of 2. Find node R 3(Y 3, y 3), Y 3 Y, y 3 Y 3. Substitute R 3(Y 3, y 3) into R(Y, y): Rs(Ys, y) = R(Y, y) R 3(Y 3, y 3), Ys = Y y 3 4. Minimize Rs(Ys, y) to get Rr(Yr, y), |Yr| ≤ |Ys| 5. Accept transformation if Rr(Yr, y) reduces the cost of 9/16/2020 IWLS 2002, New Orleans, Louisiana 9

Common Logic Extraction 1. 2. 3. 4. 5. 9/16/2020 Get several functionally related nodes Merge the nodes and derive complete flexibility, R , of the merged node Look at cofactors appearing at a window of levels in the BDD of R Find a set of compatible cofactors and express them as an MV relation Try the MV relation as a Boolean divisor of the original nodes IWLS 2002, New Orleans, Louisiana 10

Case Study: Decomposition and SAT • Ashenhurst-Curtis decomposition of multivalued relations R(A, B, v) = H( G(A, v), B, v ) – disjoint-support: A B = – support-reducing: log 2|range(G)| log 2|A| • Multi-valued SAT – Multi-valued input, binary output CNF formula – Each clause is composed of MV literals – An assignment of MV variables satisfies the CNF formula, if in each clause, there is at least one literal with a value belonging to the assignment 9/16/2020 IWLS 2002, New Orleans, Louisiana 11

SAT Variables • n variables ci, 1 i n, to encode the coloring of columns. Value j belongs to the value set of variable ci, if the corresponding column, i, can be colored with the color j. The range of ci is n/2. • m variables dij, one for each entry in the table that can take more than one value. These variables represent subsets of original values Sij, which are in agreement with the selected decomposition. The range is the range of the relation. 9/16/2020 IWLS 2002, New Orleans, Louisiana 12

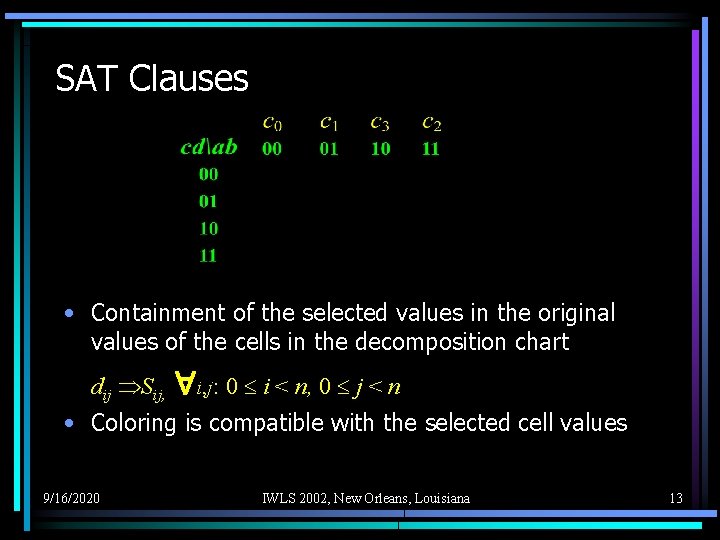
SAT Clauses • Containment of the selected values in the original values of the cells in the decomposition chart dij Sij, i, j: 0 i < n, 0 j < n • Coloring is compatible with the selected cell values 9/16/2020 IWLS 2002, New Orleans, Louisiana 13

Simplifications of SAT Problem • No need to introduce variables dij and ci: – If a column is incompatible with other columns – If two columns can only be compatible with each other • No need to introduce variable dij: – If the corresponding cell in the decomposition chart has only one value. • Using an efficient SAT solver, it may be possible to solve the decomposition problem for nodes with 8 -12 input variables 9/16/2020 IWLS 2002, New Orleans, Louisiana 14

Conclusions • Boolean paradigm – Boolean operations are applied to the MV relation representing the complete flexibility of a node derived from the network structure – An efficient implementation may be possible due to common computational cores (BDDs and SAT) and recently improved algorithms – A more general point of view reveals underlying relationships among the procedures 9/16/2020 IWLS 2002, New Orleans, Louisiana 15

Conclusions (continued) • A synthesis flow based of these methods may lead to the improvements in the optimization quality because – The use of multi-valued logic leads to searching a larger space of solutions. – Boolean (not only algebraic) properties of nodes are exploited. – The complete sets of don’t-cares (partial cares) give greater flexibility for optimizing the nodes of the network. – The SAT-based formulation is not limited to one particular encoding or coloring. – Functional decomposition can be performed concurrently with technology mapping (similar to Kravets and Sakallah, DAC’ 98). 9/16/2020 IWLS 2002, New Orleans, Louisiana 16

A Boolean Paradigm in Multi-Valued Logic Synthesis Alan Mishchenko, ECE Dept, Portland State University Robert K. Brayton, EECS Dept, UC Berkeley The goal of this work: • 1. Develop Boolean algorithms working on MV relations 2. Explore interdependence and common computational core of Boolean algorithms 3. This study is possible because of the vantage point of multivalued logic optimization 9/16/2020 • Optimization algorithms considered: – Node simplification – Partial encoding – Decomposition – Resubstitution – Common logic extraction Case study: Decomposition and SAT IWLS 2002, New Orleans, Louisiana 17