A BlockCipher Mode of Operation for Parallelizable Message
A Block-Cipher Mode of Operation for Parallelizable Message Authentication John Black University of Nevada, Reno, USA EUROCRYPT – May 1, 2002 Amsterdam, The Netherlands Phillip Rogaway University of California, Davis, USA and Chiang Mai University, Thailand
What is a MAC? AK M. s MACG: generate authentication tag G s = MACK ([IV, ] M) BK MACV: verify authentication tag V MACK (M, s) Most MACs are deterministic—they need no nonce/state/IV/$ Stateless MACs are more practical 2
![The ACMA Model [GMR, BKR] M 1 Adversary M 2 MACK(M 1) MAC Oracle](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-3.jpg "The ACMA Model [GMR, BKR] M 1 Adversary M 2 MACK(M 1) MAC Oracle")
The ACMA Model [GMR, BKR] M 1 Adversary M 2 MACK(M 1) MAC Oracle (K) MACK(M 2) Mq MACK(Mq) Adversary 3 (M*, s*) // forgery attempt
A Precise Definition We define the advantage of a “MAC adversary” A over a particular MAC algorithm M as We define the maximum advantage of any MAC adversary making at most q queries totaling at most m blocks as Our goal is to bound this quantity by a function in q and m which is “small” for “reasonable” values of q and m 4
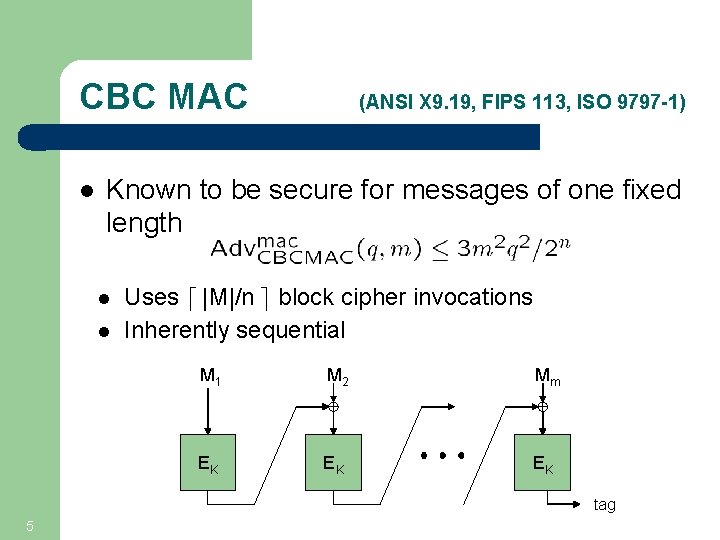
CBC MAC l (ANSI X 9. 19, FIPS 113, ISO 9797 -1) Known to be secure for messages of one fixed length l l Uses d |M|/n e block cipher invocations Inherently sequential M 1 M 2 Mm EK EK EK tag 5
Parallelizable MACs: Important? l In some settings, MAC performance is paramount – l Extracting parallelism is a simple way to achieve dramatic increases in performance – 6 Eg, a web server handling thousands of requests/sec Algorithm design governs to what extent we can parallelize l Parallelism is the only way to achieve extreme speeds in hardware or software l No disadvantage provided we do not surrender too much serial efficiency
A First Attempt: XOR MAC l l Not a PRF c ¼ 2 times as many block cipher calls as CBC MAC n-1 k Nonce k M[1] n n n k . . . M[2] M[m] n <0, Nonce> <1, M[1]> <2, M[2]> . . . <m, M[m]> EK EK EK . . . EK + Tag 7 [BGR 95]
![Protected Counter Sums l [Be 99] A PRF variant of the XOR MAC k](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-8.jpg "Protected Counter Sums l [Be 99] A PRF variant of the XOR MAC k")
Protected Counter Sums l [Be 99] A PRF variant of the XOR MAC k k M[1] M[2] n k . . . n M[m] n <1, M[1]> <2, M[2]> . . . <m, M[m]> FEKK EK . . . EK k Y[1] k k Y[m] Y[2] + n k S <0, S > FEKK k 8 Tag
![Gligor-Donescu MAC l l [GD 01] XOR MAC with better method for block offsets](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-9.jpg "Gligor-Donescu MAC l l [GD 01] XOR MAC with better method for block offsets")
Gligor-Donescu MAC l l [GD 01] XOR MAC with better method for block offsets But no longer a PRF Nonce M[1] R + + X[1] EK R EK Y[1] . . . M[2] m. R + 2 R X[2] X[m] . . . EK Y[2] EK Y[m] Å Tag 9 M[m]
PMAC: A Parallelizable MAC A Fully-Parallelizable VIL PRF: {0, 1}* {0, 1}n Cannot distinguish PMACK(¢) from a random function R(¢) Can be used as a (stateless, deterministic) MAC l Efficient – – l Simple – – l no n-bit addition or mod p operations—just xors and shifts much simpler than any known Carter-Wegman MAC Provably Secure – 10 uses d|M|/ne block cipher calls, like basic CBC MAC uses a single block cipher key low session-startup cost: about one block cipher call essentially endian neutral if E is a secure block cipher then PMAC[E] is a good PRF
![n M[1] Å n M[2] L EK Å EK . . . n M[m-1]](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-11.jpg "n M[1] Å n M[2] L EK Å EK . . . n M[m-1]")
n M[1] Å n M[2] L EK Å EK . . . n M[m-1] Å 2 L . . . possibly short M[m] (m-1)L EK Pad Å S if |M[m]| < n then 0 if |M[m]| = n then -L K ® -L L 2 L 3 L … as implicit on next slide Å S' EK Full. Tag first t bits PMAC 11 t Tag
![Definition of PMAC [E, t] algorithm PMACK )M( L(0) = EK(0) L(-1) = lsb(L(0))](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-12.jpg "Definition of PMAC [E, t] algorithm PMACK )M( L(0) = EK(0) L(-1) = lsb(L(0))")
Definition of PMAC [E, t] algorithm PMACK )M( L(0) = EK(0) L(-1) = lsb(L(0)) ? (L(0) >> 1) Å Const 43 : (L(0) >>1) for i = 1, 2, … do L(i) = msb(L(i-1)) ? (L(i-1) << 1) Å Const 87 : (L(i-1) <<1) Partition M into M[1]. . . M[m] // each n bits, except M[m] may be shorter Offset = 0 for i=1 to m-1 do Offset = Offset Å L(ntz(i)) S = S Å EK )M[i] Å Offset( S = S Å pad (M[m]) if |M[m]| = n then S = S Å L(-1) Full. Tag = EK )S ( Tag = first t bits of Full. Tag return Tag 12
![PMAC’s Security [GGM, BKR] Security as a VIL PRF Rand func oracle, R xi](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-13.jpg "PMAC’s Security [GGM, BKR] Security as a VIL PRF Rand func oracle, R xi")
PMAC’s Security [GGM, BKR] Security as a VIL PRF Rand func oracle, R xi R (xi) xi A PMACK oracle PMACK (xi) Advprf (A) = Pr[APMACK = 1] – Pr[AR = 1] 13
![Block-Cipher Security [GGM, LR, BKR] Security as a FIL PRP Rand perm oracle, p](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-14.jpg "Block-Cipher Security [GGM, LR, BKR] Security as a FIL PRP Rand perm oracle, p")
Block-Cipher Security [GGM, LR, BKR] Security as a FIL PRP Rand perm oracle, p xi p (xi) Enciphering oracle EK xi B EK (xi) Advprp (B) = Pr[BEK = 1] – Pr[Bp = 1] 14
![PMAC Theorem Suppose $ an adversary A that breaks PMAC[E] with: time = t](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-15.jpg "PMAC Theorem Suppose $ an adversary A that breaks PMAC[E] with: time = t")
PMAC Theorem Suppose $ an adversary A that breaks PMAC[E] with: time = t total-num-of-blocks = s adv = Advprf (A) Then $ an adversary B that breaks block cipher E with: time » t num-of-queries » s Advprp (B) » Advprf (A) – s 2 / 2 n-1 To wrap up, it is a standard result that any t-bit-output PRF can be used as a MAC, where the forging probability will be at most Advprf(A) + 2 -t 15
![Proof Idea M: M[1] M[2] M[3] M[m] M’[2] M’[3] M’[m’] distinct M’: M’[1] X[2]](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-16.jpg "Proof Idea M: M[1] M[2] M[3] M[m] M’[2] M’[3] M’[m’] distinct M’: M’[1] X[2]")
Proof Idea M: M[1] M[2] M[3] M[m] M’[2] M’[3] M’[m’] distinct M’: M’[1] X[2] M[2] Er. K 16 T r tag Other Stuff 2 L M’[2] Y[2] X’[2] Er. K Y’[2] T’
PMAC as a PRF Structure Lemma and PMAC Theorem: Fix n, t ¸ 1. Let A be any adversary who asks q queries, these having an aggregate length of s blocks. Then where m 1 + L + mq = s. 17
![PMAC Performance (Serial) l A moderately-optimized implementation of PMAC[AES] (Krovetz) runs in 18. 4](http://slidetodoc.com/presentation_image_h2/8832b2c2f2472d59787c4c4092c3148c/image-18.jpg "PMAC Performance (Serial) l A moderately-optimized implementation of PMAC[AES] (Krovetz) runs in 18. 4")
PMAC Performance (Serial) l A moderately-optimized implementation of PMAC[AES] (Krovetz) runs in 18. 4 cpb. Compare with 17. 1 cpb for AES. – l Aggressively-optimized basic CBC MAC runs on a Pentium at 15. 5 cpb [Lipmaa] – 18 P 3, C+assembly, gcc, 2 KB, data in L 1 cache We guess that an aggressively-optimized PMAC[AES] should run at about 16. 5 cpb.
d Ke yl ve lk o en g th rhe a le za b lel i Pa ral C F ({0, 1}n)m ü t |M| / n k 1 xor {0, 1}* ü t é|M| / nù k + 2 n 1 xor /b MA XCBC PR CBC MAC Do ma in len g th Comparisons [BR 00] XECB-MAC {0, 1}* t+n ü é|M| / nù + varies 1 xor 2 add t ü é|M| / nù k 3 xor (3 versions) [GD 00, 01] PMAC [BR 02] 19 {0, 1}* ü
Implementation Effort 20 Object Effort (John-Time) Basic CBC MAC 30 mins XCBC 1 hour PMAC 3 hours OCB 4 hours AES 8 hours DES 8 hours UMAC 3 days
More Information on PMAC Visit the PMAC web page www. cs. ucdavis. edu/~rogaway/pmac Web page contains: Reference Code (by Ted Krovetz and me) Test Vectors FAQ Full version of the PMAC paper 21
- Slides: 21