A Binary Search Tree with 6 Levels 50

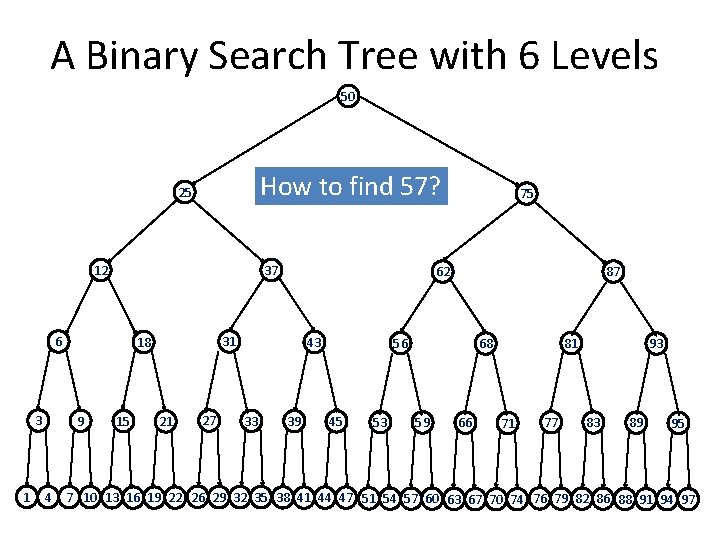
A Binary Search Tree with 6 Levels 50 How to find 57? 25 12 37 6 3 1 9 15 62 31 18 21 27 43 33 75 39 87 56 45 53 81 68 59 66 71 77 93 83 89 95 4 7 10 13 16 19 22 26 29 32 35 38 41 44 47 51 54 57 60 63 67 70 74 76 79 82 86 88 91 94 97

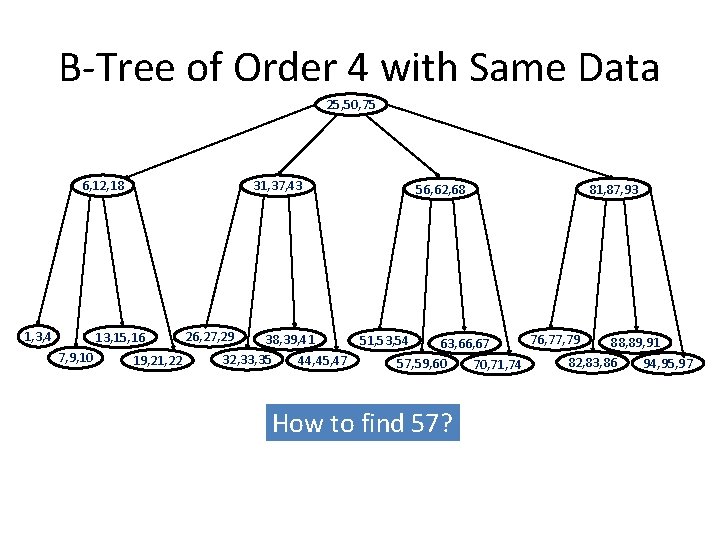
B-Tree of Order 4 with Same Data 25, 50, 75 6, 12, 18 1, 3, 4 31, 37, 43 13, 15, 16 7, 9, 10 19, 21, 22 56, 62, 68 26, 27, 29 81, 87, 93 38, 39, 41 76, 77, 79 51, 53, 54 88, 89, 91 63, 66, 67 32, 33, 35 44, 45, 47 82, 83, 86 57, 59, 60 94, 95, 97 70, 71, 74 How to find 57?

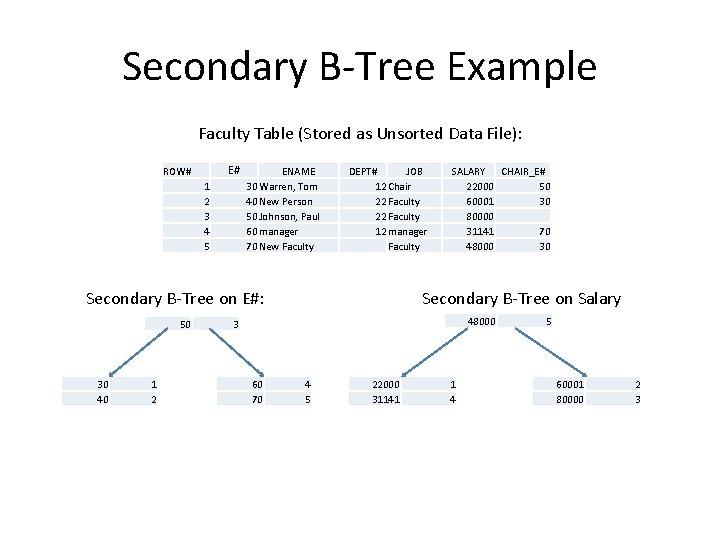
Secondary B-Tree Example Faculty Table (Stored as Unsorted Data File): E# ROW# 1 2 3 4 5 ENAME 30 Warren, Tom 40 New Person 50 Johnson, Paul 60 manager 70 New Faculty DEPT# JOB 12 Chair 22 Faculty 12 manager Faculty Secondary B-Tree on E#: 50 30 40 1 2 SALARY CHAIR_E# 22000 50 60001 30 80000 31141 70 48000 30 Secondary B-Tree on Salary 48000 3 60 70 4 5 22000 31141 1 4 5 60001 80000 2 3

Primary or Clustered B-Tree Example on E# 50 Johnson, Paul 30 Warren, Tom 40 New Person 12 Chair 22 Faculty 22000 60001 22 Faculty 50 30 80000 60 manager 70 New Faculty 12 manager Faculty • No unsorted data file. • No B-Tree is now possible on salary; why? 31141 48000 70 30

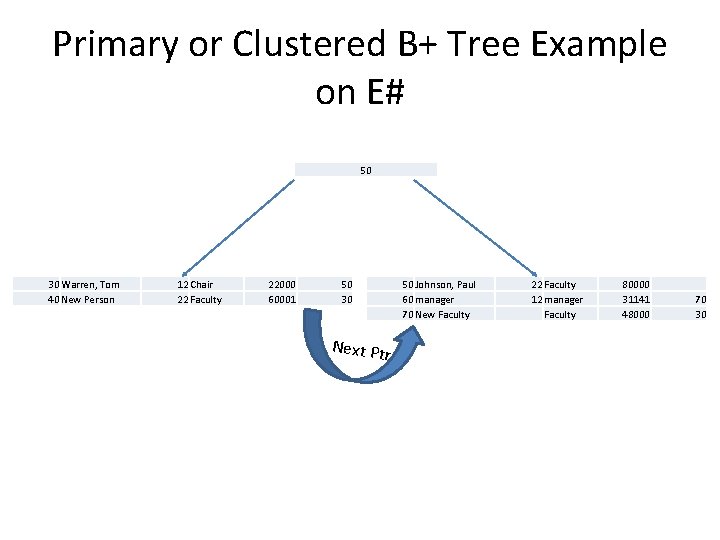
Primary or Clustered B+ Tree Example on E# 50 30 Warren, Tom 40 New Person 12 Chair 22 Faculty 22000 60001 50 30 Next Ptr 50 Johnson, Paul 60 manager 70 New Faculty 22 Faculty 12 manager Faculty 80000 31141 48000 70 30