A Binary Linear Programming Formulation of the Graph

A Binary Linear Programming Formulation of the Graph Edit Distance Authors: Derek Justice & Alfred Hero (PAMI 2006) Presented by Shihao Ji Duke University Machine Learning Group July 17, 2006

Outline • Introduction to Graph Matching • Proposed Method (binary linear program) • Experimental Results (chemical graph matching)

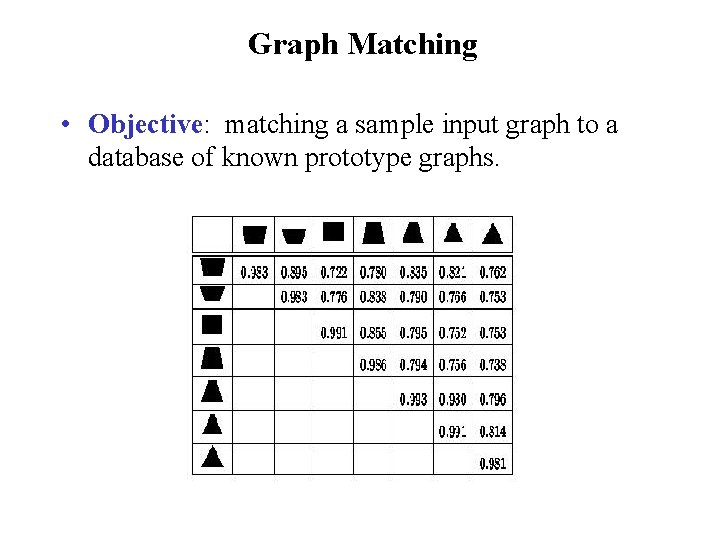
Graph Matching • Objective: matching a sample input graph to a database of known prototype graphs.

Graph Matching (cont’d) • A real example: face identification

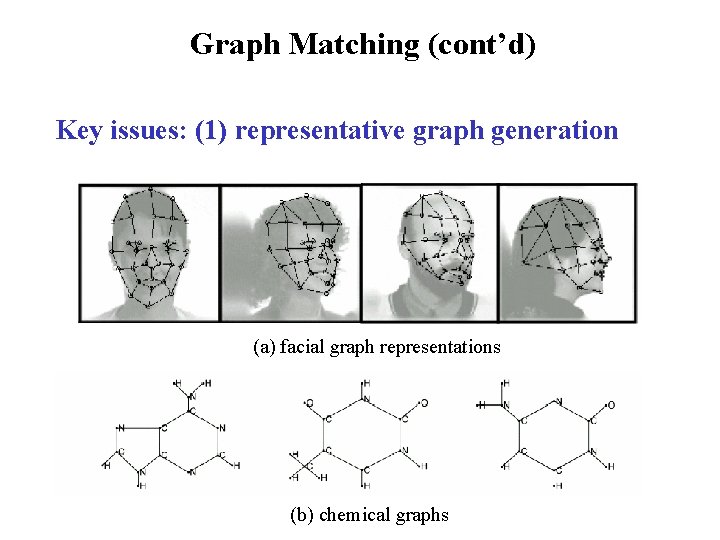
Graph Matching (cont’d) Key issues: (1) representative graph generation (a) facial graph representations (b) chemical graphs

Graph Matching (cont’d) Key issues: (2) graph distance metrics q Maximum Common Subgraph (MCS) q Graph Edit Distance (GED) Enumeration procedures (for small graphs) Probabilistic models (MAP estimates) Binary Linear Programming (BLP)

Graph Edit Distance • Basic idea: define graph edit operations (such as insertion or deletion or relabeling of a vertex) along with costs associated with each operation. • The GED between two graphs is the cost associated with the least costly series of edit operations needed to make the two graph isomorphic. • Key issues: how to find the least costly series of edit operations? how to define edit costs?

Graph Edit Distance (cont’d) • How to compute the distance between G 0 and G 1? • Edit Grid

Graph Edit Distance (cont’d) • Isomorphisms of G 0 on the edit grid standard placement • State Vectors

Graph Edit Distance (Cont’d) • Definition: (if the cost function c is a metric) • Objective function: binary linear program (NP-hard!!!)

Graph Edit Distance (cont’d) • Lower bound: linear program (polynomial time) • Upper bound: assignment problem (polynomial time)

Edit Cost Selection • Goal: suppose there is a set of prototype graphs {Gi} i=1, …, N and we classify a sample graph G 0 by a nearest neighbor classifier in the metric space defined by the graph edit distance. • Prior informaiton: the prototypes should be roughly uniformly distributed in the metric space of graphs. • Why: it minimizes the worst case classification error since it equalizes the probability of error under a nearest neighbor classifier.

Edit Cost Selection (cont’d) • Objective: minimize the variance of pairwise NN distances • Define unit cost function, i. e. , c(0, 1)=1, c(a, b)=1, c(a, a)=0 • Solve the BLP (with unit cost) and find the NN pair • Construct Hk, i = the number of ith edit operation for the kth NN pair • • Objective function: (convex optimization)

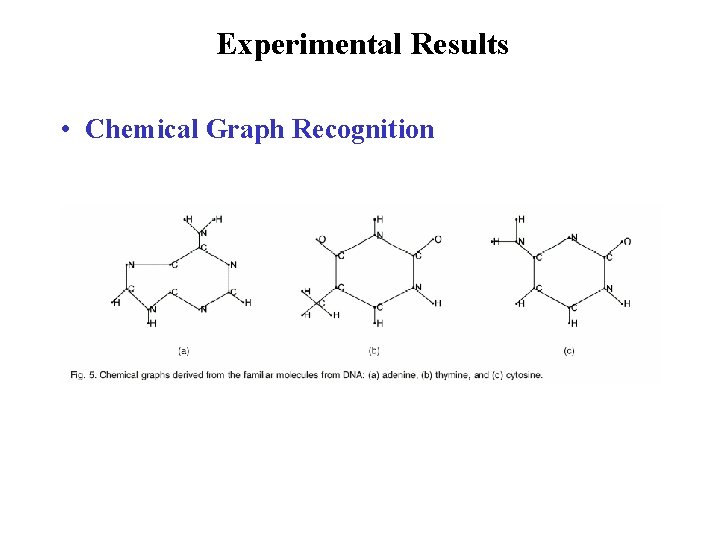
Experimental Results • Chemical Graph Recognition

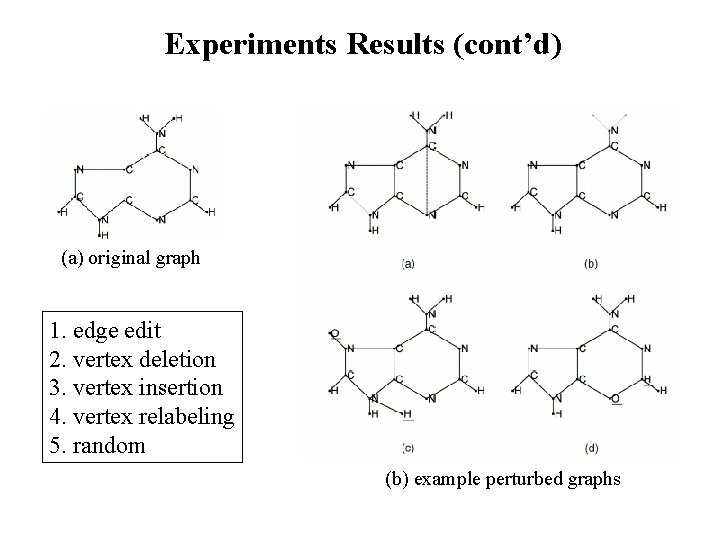
Experiments Results (cont’d) (a) original graph 1. edge edit 2. vertex deletion 3. vertex insertion 4. vertex relabeling 5. random (b) example perturbed graphs

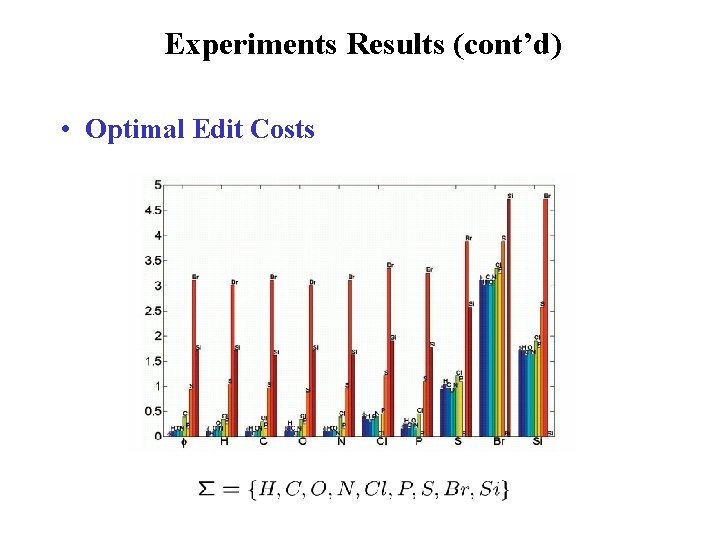
Experiments Results (cont’d) • Optimal Edit Costs

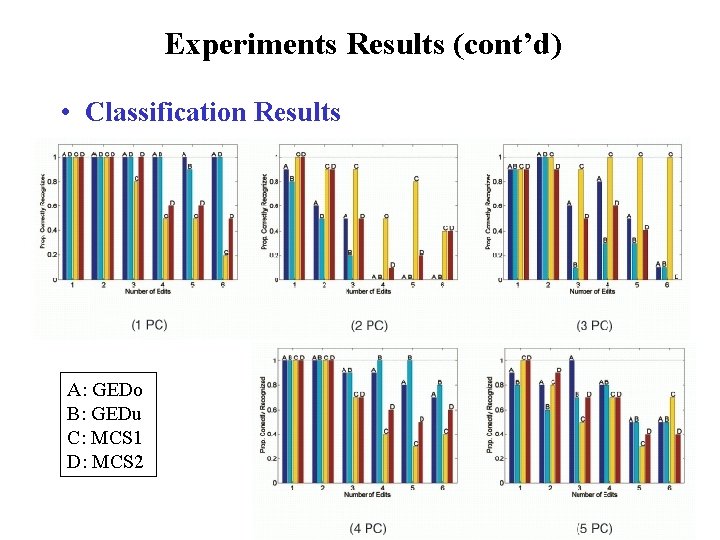
Experiments Results (cont’d) • Classification Results A: GEDo B: GEDu C: MCS 1 D: MCS 2

Conclusion • Present a binary linear programming formulation of the graph edit distance; • Offer a minimum variance method for choosing a cost metric; • Demonstrate the utility of the new method in the context of a chemical graph recognition.