A Bifurcation Analysis of a Differential Equations Model

A Bifurcation Analysis of a Differential Equations Model for Mutualism Bruce Peckham Department of Mathematics and Statistics University of Minnesota Duluth Collaborators: Wendy Gruner Graves Rainy River Community College John Pastor Department of Biology, University of Minnesota Duluth B. Peckham 2005 SIAM D. S.

Abbreviated History of 2 -species Mutualism Models • 1978 Vandermeer and Boucher, J. Theor. Biol. Description of different dynamics for Lotka-Volterra (LV) model – Weak mutualism: populations survive at slightly higher populations than on their own – Strong mutualism: threshold for obligate models, but unbounded growth; “bend” isoclines to prevent unbounded growth. • 1983 A. Dean Limited Carrying Capacity (LCC) model – Weak: same as LV – Strong: singularity when either species is obligate • 2004 The limited growth rate (LGR) model – Weak mutualism: same as LV – Strong mutualism: threshold for obligate models, but no unbounded growth – Allows for smooth transitions between facultative and obligate B. Peckham 2005 SIAM D. S. 2

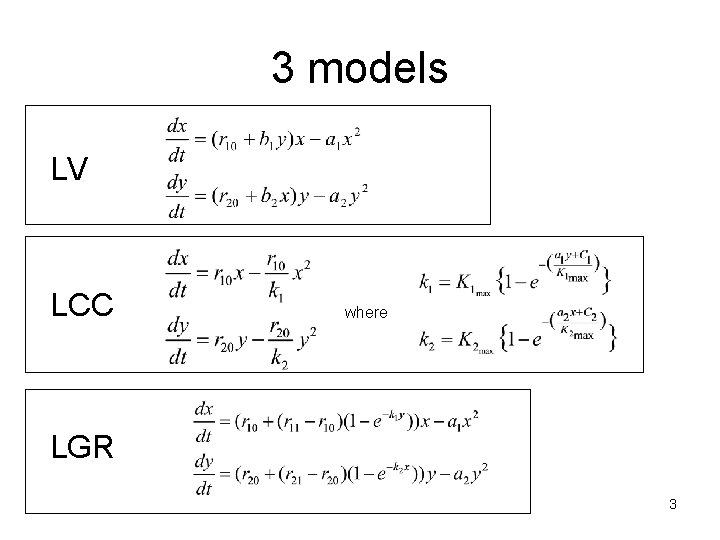
3 models LV LCC where LGR 3

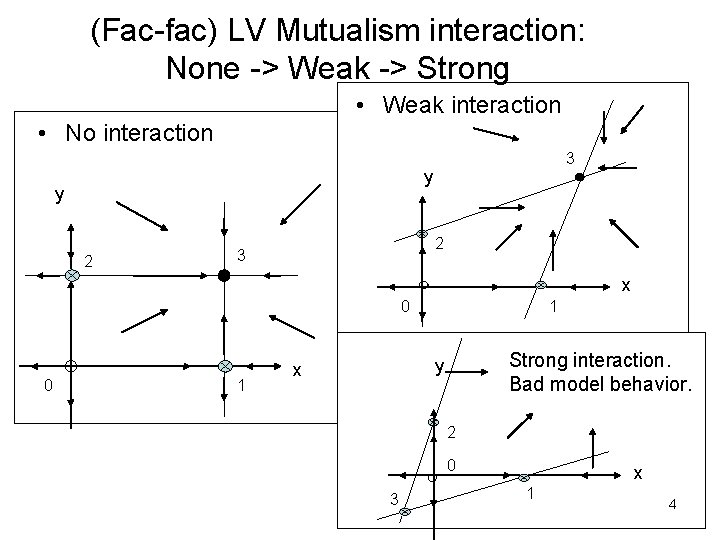
(Fac-fac) LV Mutualism interaction: None -> Weak -> Strong • Weak interaction • No interaction 3 y y 2 2 3 x 1 0 0 1 Strong interaction. Bad model behavior. y x 2 0 3 x 1 4

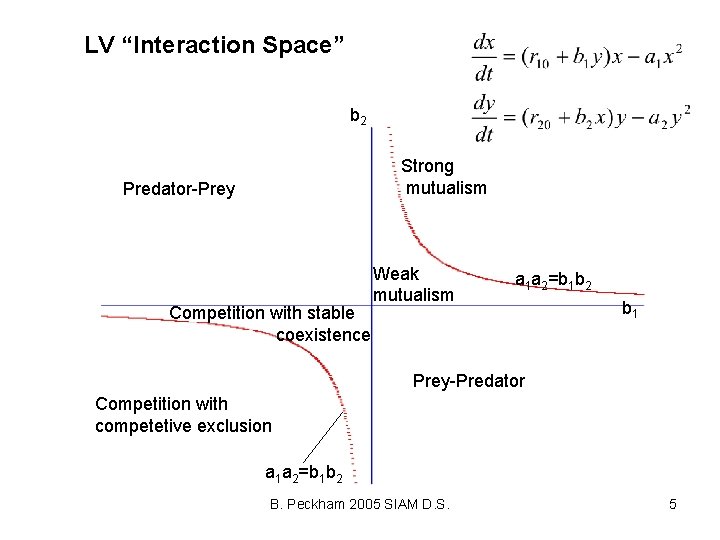
LV “Interaction Space” b 2 Strong mutualism Predator-Prey Competition with stable coexistence Weak mutualism a 1 a 2=b 1 b 2 b 1 Prey-Predator Competition with competetive exclusion a 1 a 2=b 1 b 2 B. Peckham 2005 SIAM D. S. 5

New Limited Growth Rate (LGR) Model Derivation A 1: The logistic assumption: Each species behaves according to the logistic model. A 2: The growth rate assumption: Each species affects the other species’ per capita growth rate, but not its self limitation. A 1 and A 2 imply: B. Peckham 2005 SIAM D. S. 6

LGR Model Derivation (continued) A 3: The mutualism assumption: The increase in each species cannot harm the other species. A 4: The limited benefit assumption: There is a maximum per capita growth rate attainable for each species. A 5: The proportional benefit assumption: The marginal rate of change of the per capita growth rate of each species due to the increase of the other species is proportional to the difference between the maximum growth rate and the current growth rate. A 4 and A 5 imply: R 1’(y)=k 1(r 11 – R 1(y)) and R 2’(x)=k 2(r 21 – R 2(x)) Intro DE Class !! B. Peckham 2005 SIAM D. S. 7

LGR Model Derivation (continued) Solve: A 3 implies r 11>r 10, and r 21>r 20. Resulting “Limited per capita growth rate” model: B. Peckham 2005 SIAM D. S. 8

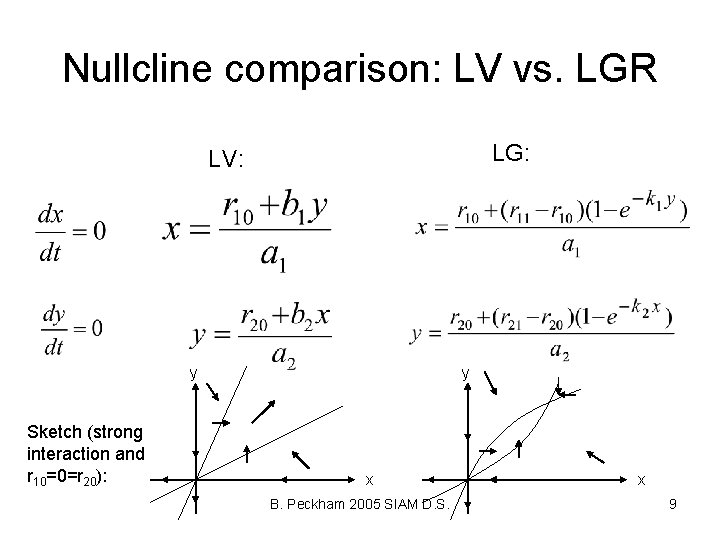
Nullcline comparison: LV vs. LGR LG: LV: y Sketch (strong interaction and r 10=0=r 20): y x B. Peckham 2005 SIAM D. S. x 9

Local reduction of LGR to LV Start with LGR: Expand exponential terms in a power series, …. Get LV + h. o. t. B. Peckham 2005 SIAM D. S. 10

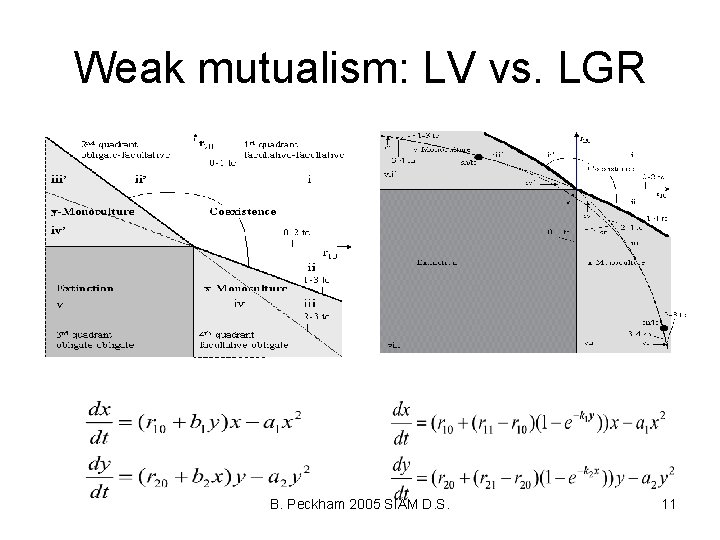
Weak mutualism: LV vs. LGR B. Peckham 2005 SIAM D. S. 11

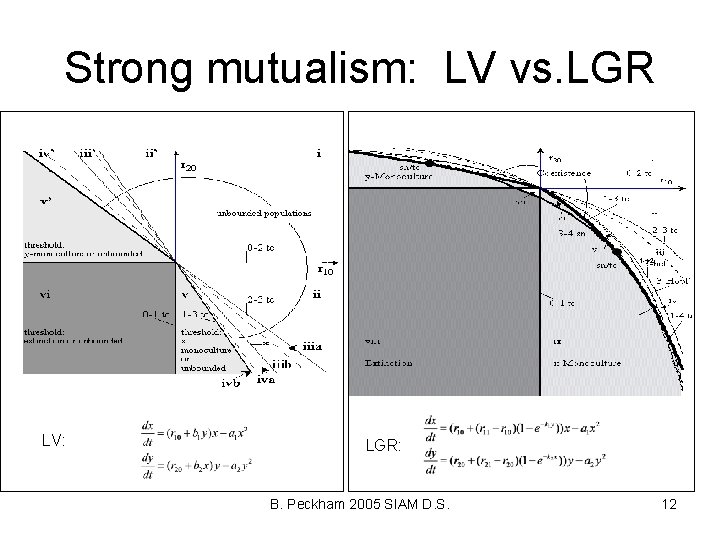
Strong mutualism: LV vs. LGR 1 ->2 LV: LGR: B. Peckham 2005 SIAM D. S. 12

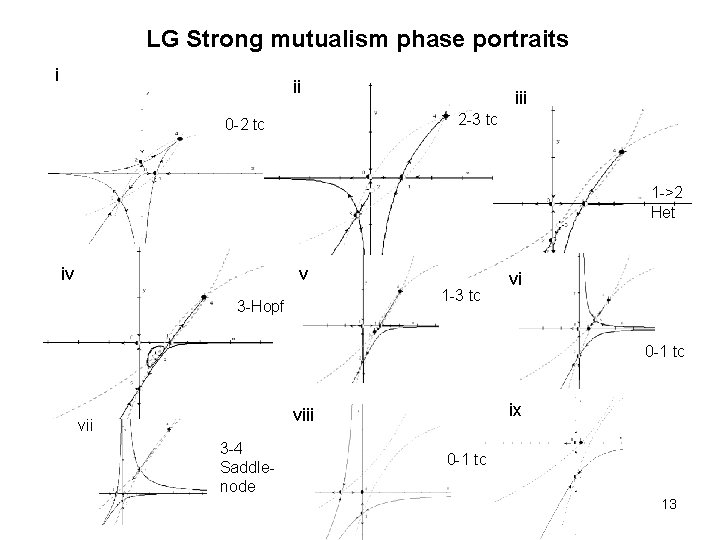
LG Strong mutualism phase portraits i ii iii 2 -3 tc 0 -2 tc 1 ->2 Het iv v 1 -3 tc 3 -Hopf vi 0 -1 tc ix viii vii 3 -4 Saddlenode 0 -1 tc 13

1 -3 Transcritical Bifurcation V: Fac-obl coexistence w/o threshold Vi: Fac-obl coexistence w/o threshold B. Peckham 2005 SIAM D. S. 14

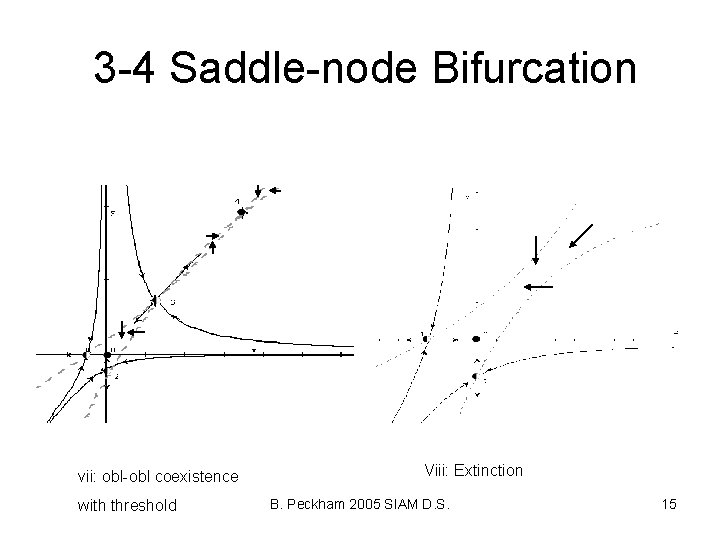
3 -4 Saddle-node Bifurcation vii: obl-obl coexistence with threshold Viii: Extinction B. Peckham 2005 SIAM D. S. 15

Mutualism in Nature • Nitrogen-fixing bacteria with plants – Example: Lichens - Cyanobacteria with fungus • Each enhances the other’s growth rate. – Bacteria produces Nitrogen for fungus – Fungus produces Photosynthate for bacteria • Environmental conditions can be adjusted to change between facultative and obligate B. Peckham 2005 SIAM D. S. 16

Unfinished Work • Local unfolding of codimension-3 point: two parameters we used plus one which controls weak vs. strong mutualism • Local unfoldings of codimension-two points with special symmetries (x=0 or y=0 invariant) • Complete classification of primary parameter space bifurcation diagrams in the “auxiliary” parameter space • Validation with experiment? ? B. Peckham 2005 SIAM D. S. 17

Summary I • The LV model is fine for weak mutualism, but not for strong mutualism. • Dean’s model is fine for facultative mutualism, but not for obligate mutualism. • The LG model works for weak/strong and facultative/obligate cases. • Small chance of obligate-obligate mutualism in nature? B. Peckham 2005 SIAM D. S. 18

Summary II • Model building is an iterative process. • Simple models can have interesting behavior • “Unrealistic” bifurcations (not in quad 1 of phase space) set up “realistic” bifurcations. Vague analogue of complex #’s. • Mathematics is more interesting than real life. • Don’t divide by zero. B. Peckham 2005 SIAM D. S. 19

A Bifurcation Analysis of a Differential Equations Model for Mutualism Bruce Peckham Department of Mathematics and Statistics University of Minnesota Duluth Collaborators: Wendy Gruner Graves Rainy River Community College John Pastor Department of Biology, University of Minnesota Duluth B. Peckham 2005 SIAM D. S.

B. Peckham 2005 SIAM D. S. 21

The 1 D logistic equation Phase Portraits: r = b – d > 0: survival x 0 R = b - d < 0: extinction r/a x r/a 0 B. Peckham 2005 SIAM D. S. 22

The 2 D Lotka-Volterra Model • Competition, Predator-Prey, Mutualism B. Peckham 2005 SIAM D. S. 23

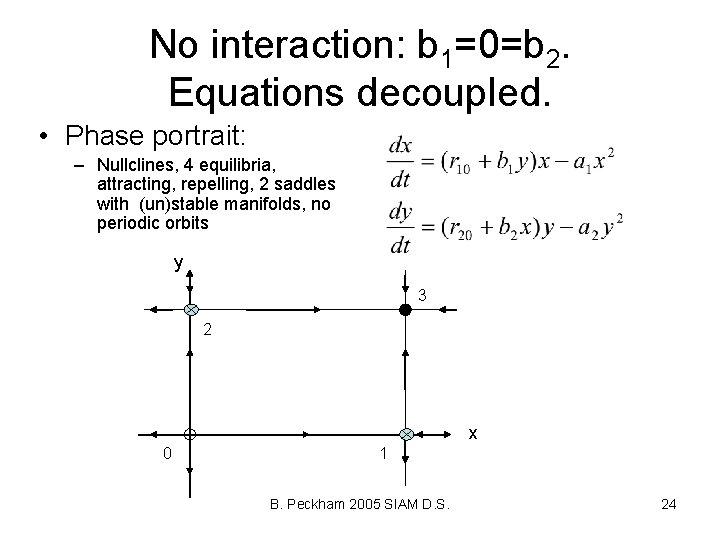
No interaction: b 1=0=b 2. Equations decoupled. • Phase portrait: – Nullclines, 4 equilibria, attracting, repelling, 2 saddles with (un)stable manifolds, no periodic orbits y 3 2 x 0 1 B. Peckham 2005 SIAM D. S. 24

Weak LV Mutualism: a 1 a 2>b 1 b 2 B. Peckham 2005 SIAM D. S. 25

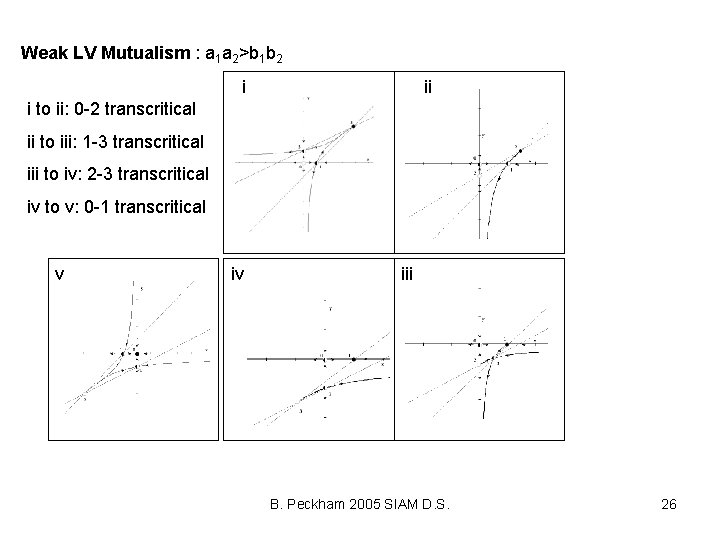
Weak LV Mutualism : a 1 a 2>b 1 b 2 i ii i to ii: 0 -2 transcritical ii to iii: 1 -3 transcritical iii to iv: 2 -3 transcritical iv to v: 0 -1 transcritical v iv iii B. Peckham 2005 SIAM D. S. 26

Skip? ? ? i v viii B. Peckham 2005 SIAM D. S. 27

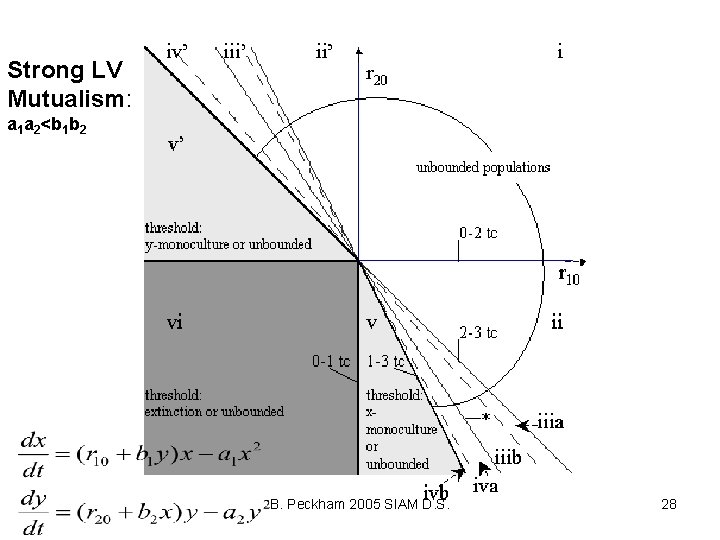
Strong LV Mutualism: a 1 a 2<b 1 b 2 B. Peckham 2005 SIAM D. S. 28

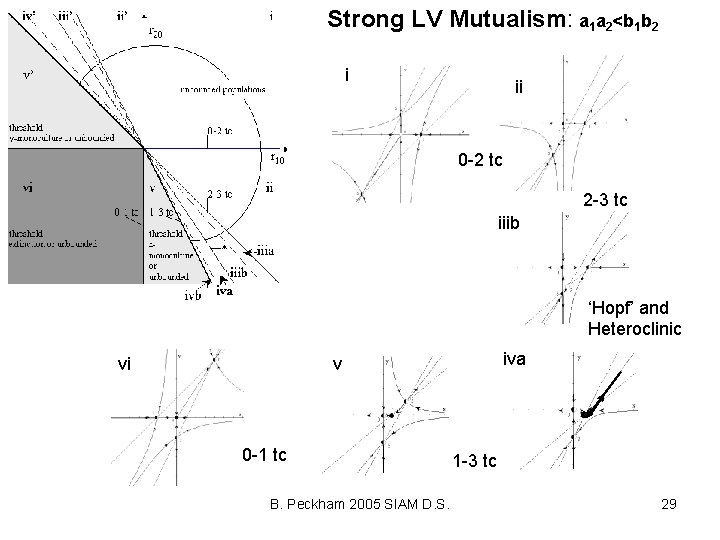
Strong LV Mutualism: a 1 a 2<b 1 b 2 i ii 0 -2 tc 2 -3 tc iiib ‘Hopf’ and Heteroclinic vi iva v 0 -1 tc B. Peckham 2005 SIAM D. S. 1 -3 tc 29

What went wrong with the Dean Model? ? A simple analogy of a singularity from the 1 D logistic DE: Phase Portraits: r>0, a>0 k>0: survival x 0 k k<0: extinction? ? x k 0 B. Peckham 2005 SIAM D. S. 30

Dean’s Model Singularities: B. Peckham 2005 SIAM D. S. 31

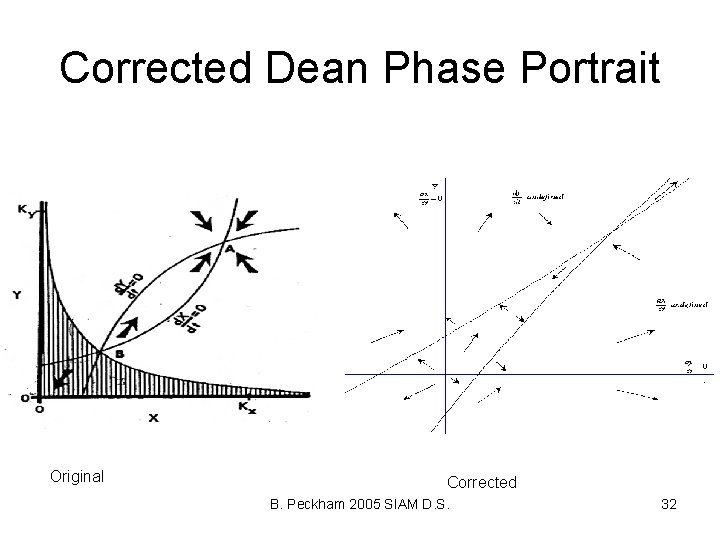
Corrected Dean Phase Portrait Original Corrected B. Peckham 2005 SIAM D. S. 32

Mutualism with limited per capita growth rate: Preview of new model. Details later. Complicated-looking growth rate term. B. Peckham 2005 SIAM D. S. 33