A BetaViscosity Model for the Evolving Solar Nebula

A Beta-Viscosity Model for the Evolving Solar Nebula Sanford S Davis Workshop on Modeling the Structure, Chemistry, and Appearance of Protoplanetary Disks 13 -17 April, 2004 Ringberg, Baveria, Germany S. Davis, April 2004

Outline of Talk l Review of the viscosity model l Global behavior of and turbulence models l Unsteady surface density model applied to a Solar Nebula l Condensation front migration in an early Solar Nebula S. Davis, April 2004

The Gaseous Nebula Evolves and Cools Hot Nebula (t ~ 102 yrs) Cool Nebula (t ~ 106 yrs) S. Davis, April 2004

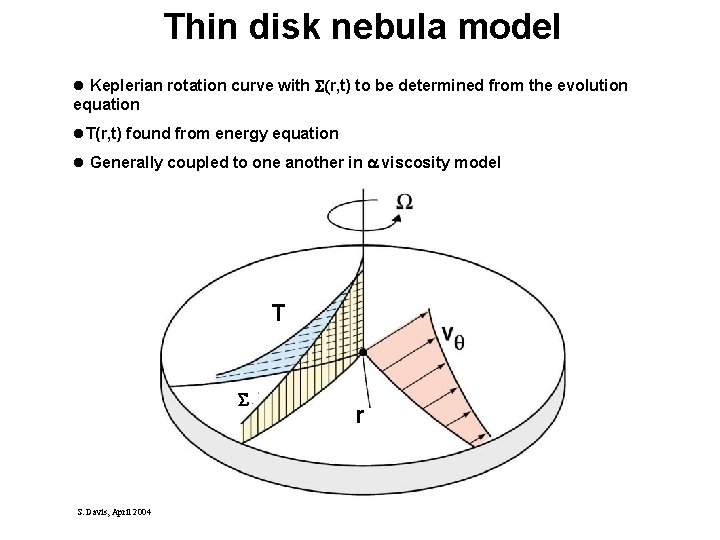
Thin disk nebula model l Keplerian rotation curve with (r, t) to be determined from the evolution equation l. T(r, t) found from energy equation l Generally coupled to one another in viscosity model T S. Davis, April 2004 r

Turbulence Model Characteristics l n is proportional to the product of a length and velocity scale (H, c) or (H, Uk) l H and r related: H ~ 5% r l c and Uk are problematic l c: random energy; Uk directed energy; turbulence velocity scale is in between l. The factors and reflect choice of scales. model used since 1970 s. model based on scaling of hydrodynamic sources of turbulence (Richard & Zahn 1999) S. Davis, April 2004

Why use a β model? l Exclude thermodynamics from the evolution equation (opacity model is not a factor) l Turbulence modeling is historically an incompressible hydrodynamic problem l Temperature follows from radiation transfer (energy equations) l As a vehicle for moving to multiphysics problems l Described in Davis (2003, Ap. J) S. Davis, April 2004

The Basic Dynamic equation Evolution depends on choice of kinematic viscosity Conventional viscosity model: viscosity model S. Davis, April 2004

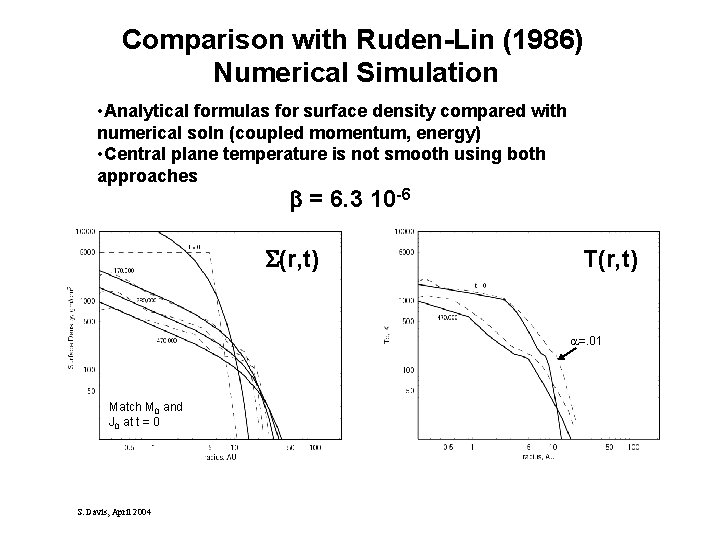
Comparison with Ruden-Lin (1986) Numerical Simulation • Analytical formulas for surface density compared with numerical soln (coupled momentum, energy) • Central plane temperature is not smooth using both approaches = 6. 3 10 -6 (r, t) T(r, t) a=. 01 Match M 0 and J 0 at t = 0 S. Davis, April 2004

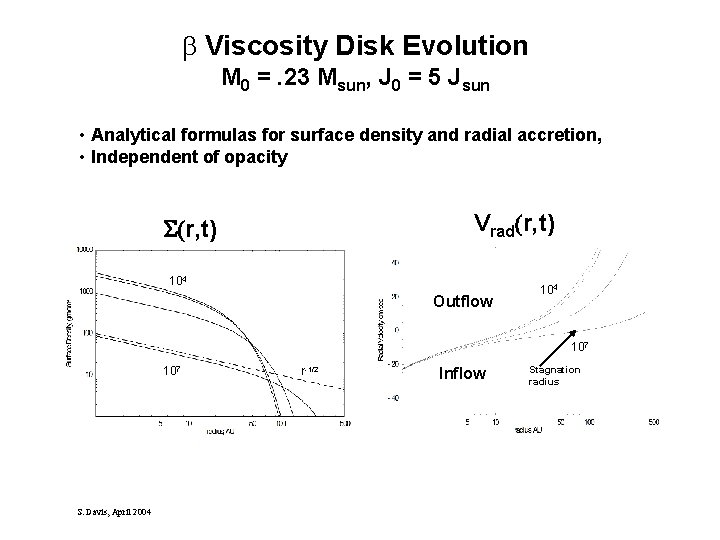
b Viscosity Disk Evolution M 0 =. 23 Msun, J 0 = 5 Jsun • Analytical formulas for surface density and radial accretion, • Independent of opacity Vrad(r, t) 104 Outflow 104 107 S. Davis, April 2004 r-1/2 Inflow Stagnation radius

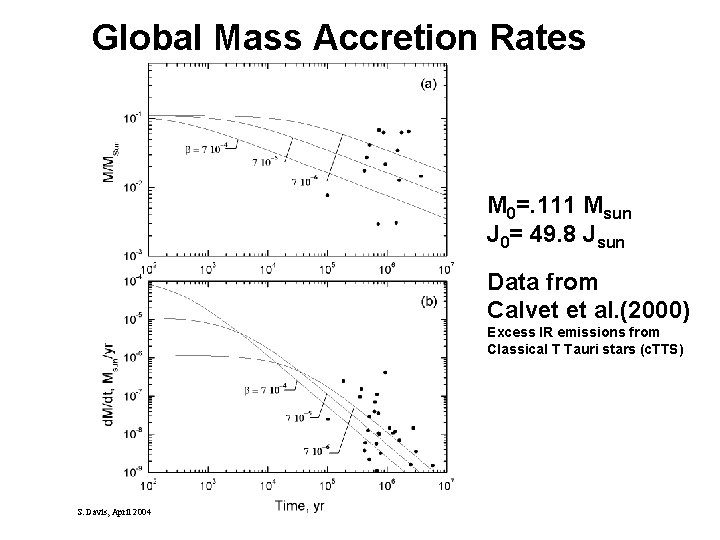
Global Mass Accretion Rates M 0=. 111 Msun J 0= 49. 8 Jsun Data from Calvet et al. (2000) Excess IR emissions from Classical T Tauri stars (c. TTS) S. Davis, April 2004

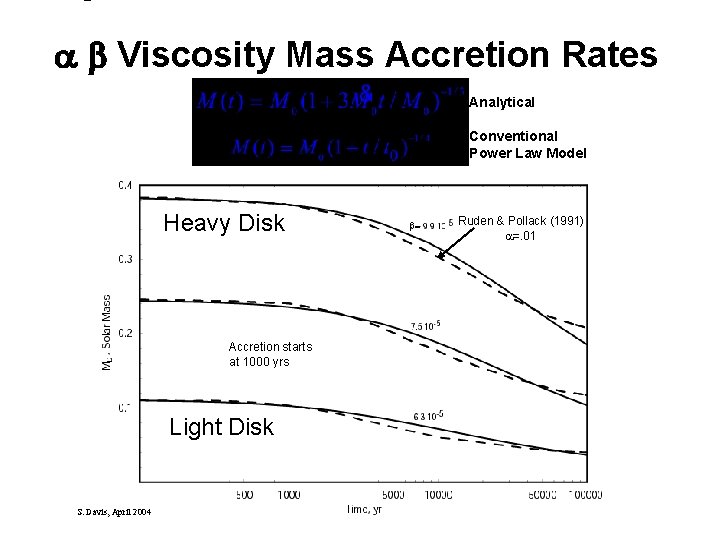
Viscosity Mass Accretion Rates Analytical Conventional Power Law Model Heavy Disk Accretion starts at 1000 yrs Light Disk S. Davis, April 2004 b= Ruden & Pollack (1991) a=. 01

Application of the Evolution Equation l What is an appropriate M 0, J 0, and ? l How well can it predict the early evolution of our Solar System? Procedure: l Fit an analytical curve (tan-1) to the total mass vs r distribution. This is the monotonic cumulative mass distribution, M(r). l Divide the incremental mass M = d. M/dr r by the incremental area A = 2 r r to obtain (r) for the ground-up planets S. Davis, April 2004

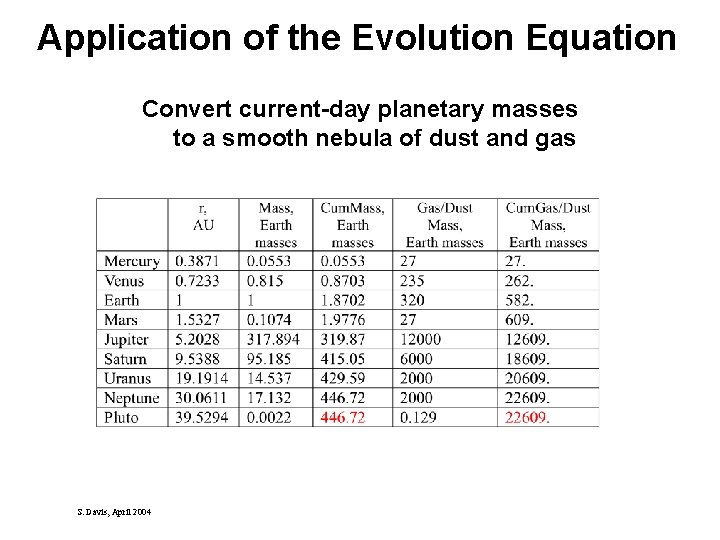
Application of the Evolution Equation Convert current-day planetary masses to a smooth nebula of dust and gas S. Davis, April 2004

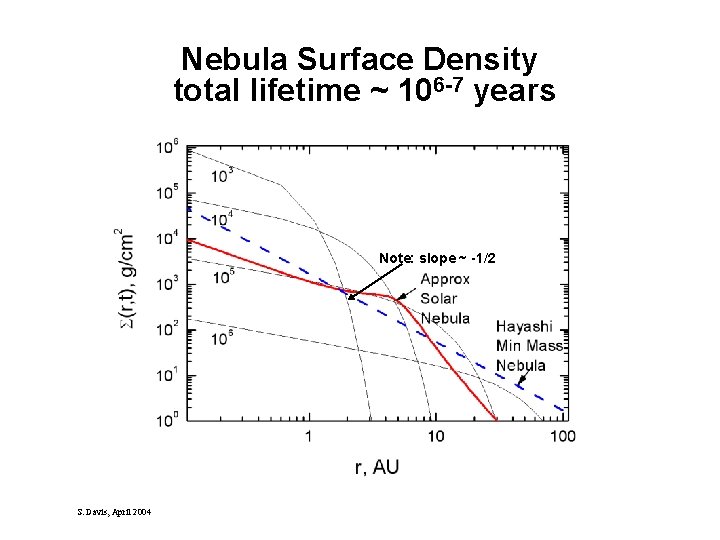
Nebula Surface Density total lifetime ~ 106 -7 years Note: slope ~ -1/2 S. Davis, April 2004

Evolution of a Condensation Front l Recent work shows that radial drift across H 2 O condensation front at 5 AU may enhance water vapor content and contribute to Jupiter’s growth. l Sweep of condensation front across the nebula may help in solidifying moderately volatile species for subsequent planetary formation. l. The viscosity formulation can be a useful tool in this interdisciplinary field l Use a quasi steady model with Mdot variable l Includes viscous heating and central star luminosity so that T = (Tv 4 + Tcs 4 )1/4 S. Davis, April 2004

Application of the Evolution Equation: Gas/Solid Sublimation Fronts Rate of increase of a solid species (Water ice, Ammonia ice, Carbon Dioxide ice) is governed by the Hertz-Knudsen relation p. Xgas is the partial pressure of species X at a given and T (from eqn) p. Xvap is the vapor pressure of species X at a given T (from tables) At equilibrium, p. Xgas = p. Xvap, solve for eq Teq and the corresponding radius req. S. Davis, April 2004

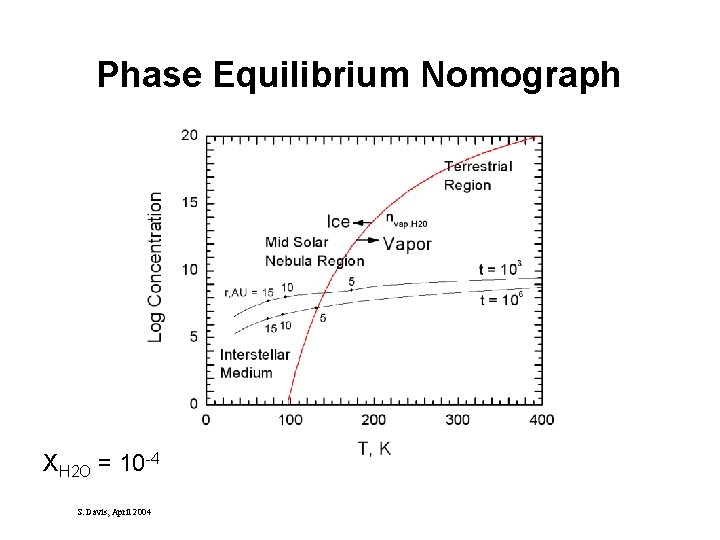
Phase Equilibrium Nomograph XH 2 O = 10 -4 S. Davis, April 2004

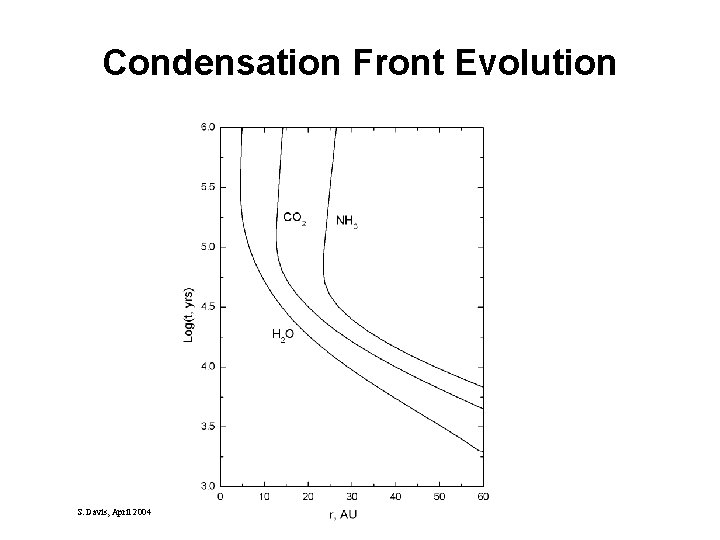
Condensation Front Evolution S. Davis, April 2004

Conclusions l. Characterization of the dynamic field is important for Chemistry: outer region hot at early times Inter-radial transfer processes: space-time regime of inflow/outflow l. The viscosity can be a useful tool in addressing multiphysics problems S. Davis, April 2004