A Bayesian statistical method for particle identification in

A Bayesian statistical method for particle identification in shower counters IX International Workshop on Advanced Computing and Analysis Techniques in Physics Research December 1 -5, 2003 N. Takashimizu 1, A. Kimura 2, A. shibata 3 and T. Sasaki 3 1 Shimane University 2 Ritsumeikan University 3 High Energy Accelerator Research Organization 1

Introduction • We made an attempt to identify particle using Bayesian statistical method. • The particle identification will be possible by extracting pattern of showers because the energy distribution differ with incident particle or energy. • Using Bayesian method in addition to the existing particle identification method, the improvement of experimental precision is expected. 2

Bayes’ Theorem • Bayes’ theorem is a simple formula which gives the probability of a hypothesis H from an observation A. • We can calculate the conditional probability of H which causes A as follows. – P(A|H) : The probability of A given by H – P(H) : The probability prior to the observations – P(A) : The probability of A whether H is true or not • Bayes’ theorem gives a learning system how to update parameters after observing A. 3

Bayesian Estimation • Bayesian estimation is a statistical method based on the Bayes’ theorem. – Think of unknown parameters as probability variables and give them density distributions instead of estimating particular value. • Represent information about parameters as prior distribution p（θ，x）before we make observations. – Generally the prior distribution is not sharp because our knowledge about parameter is insufficient before observation. 4

Bayesian Estimation • When we make an observation the posterior distribution can be calculated by using both data generation model and prior distribution. • The predictive distribution of the future observation based on the observed data x=（x 1，x 2，…xn） is the expectation of the model for all possible posterior distribution. 5

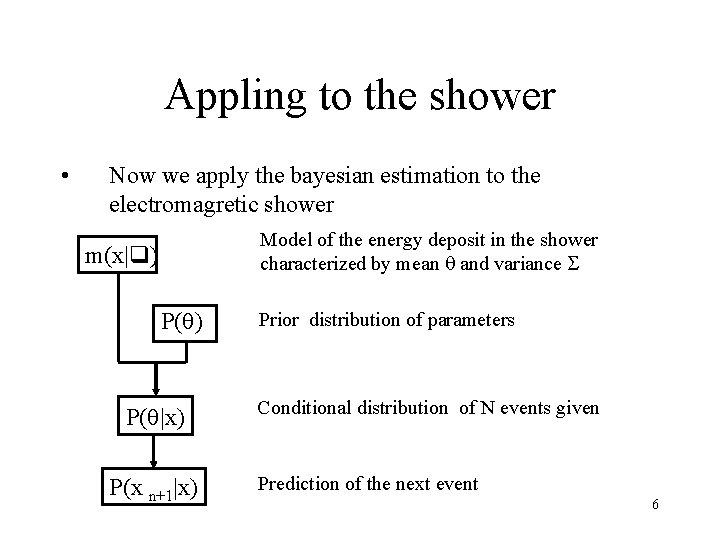
Appling to the shower • Now we apply the bayesian estimation to the electromagretic shower Model of the energy deposit in the shower characterized by mean q and variance S m(x|q) P(q|x) P(x n+1|x) Prior distribution of parameters Conditional distribution of N events given Prediction of the next event 6

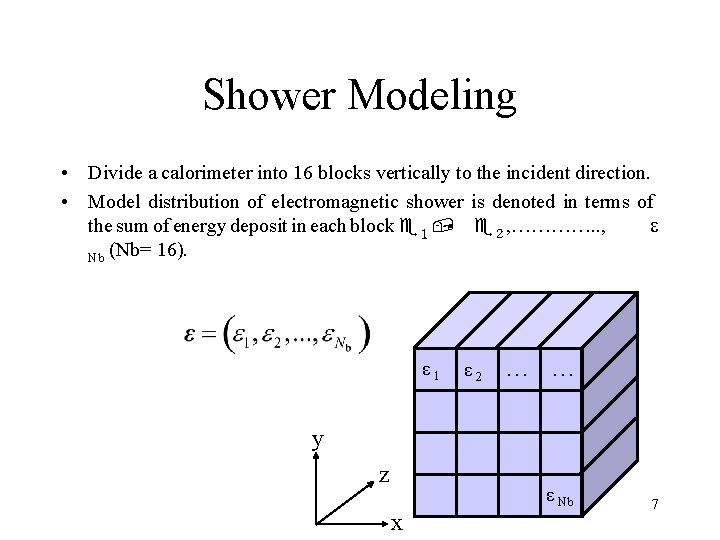
Shower Modeling • Divide a calorimeter into 16 blocks vertically to the incident direction. • Model distribution of electromagnetic shower is denoted in terms of the sum of energy deposit in each block e１, e２, …………. . , e Nb (Nb= 16). ε 1 ε 2 … … y z x ε Nb 7

Model Distribution • If the shape of the shower e is multivariate normal distribution N(θ, Σ) then the model is presented as • When the shower is caused by particle f with incident energy E 0 the model above is represented by • To simplify the calculation we assume there is no correlation among energy deposit in each block. 8

Model Distribution • After N observation the model will be a joint probability density 9

Posterior Distribution • When we assume prior distribution is uniform, it is given by • The posterior distribution is given in terms of the model and the prior distribution when observing n showers caused by f, E 0 10

Predictive Distribution • Finally the next shower can be predicted on condition that n- shower, particle and incident energy are known. 11

Particle Identification • Given the next shower the conditional probability for occurrence of that shower is obtained from the predictive distribution. • Selecting the most probable condition, that is, a parameter set of f and E 0, enable us the particle identification. 12

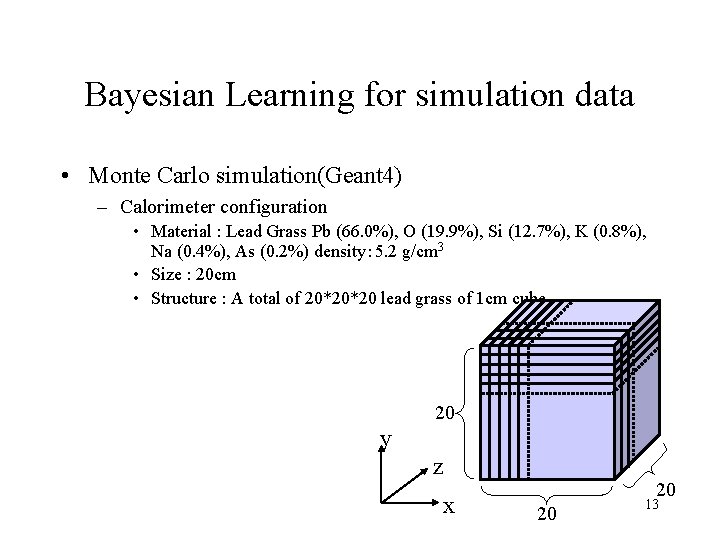
Bayesian Learning for simulation data • Monte Carlo simulation(Geant 4) – Calorimeter configuration • Material : Lead Grass Pb (66. 0%), O (19. 9%), Si (12. 7%), K (0. 8%), Na (0. 4%), As (0. 2%) density： 5. 2 g/cm 3 • Size : 20 cm • Structure : A total of 20*20*20 lead grass of 1 cm cube 20 y z x 20 20 13

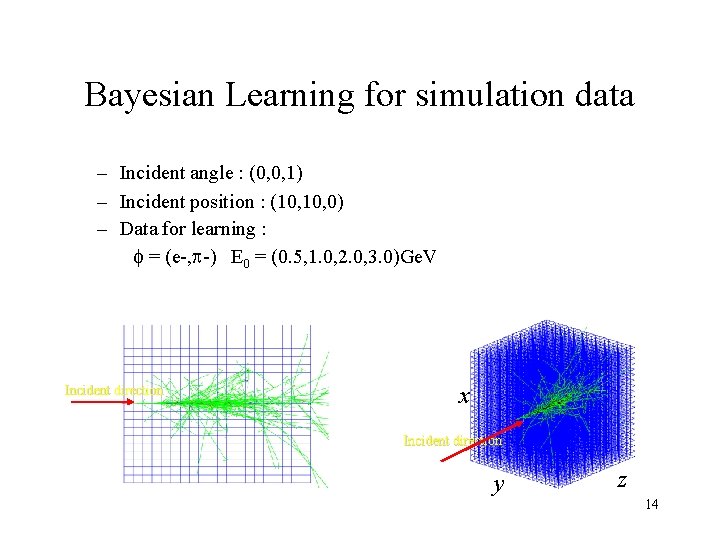
Bayesian Learning for simulation data – Incident angle : (0, 0, 1) – Incident position : (10, 0) – Data for learning : f = (e-, p-) E 0 = (0. 5, 1. 0, 2. 0, 3. 0)Ge. V Incident direction x Incident direction y z 14

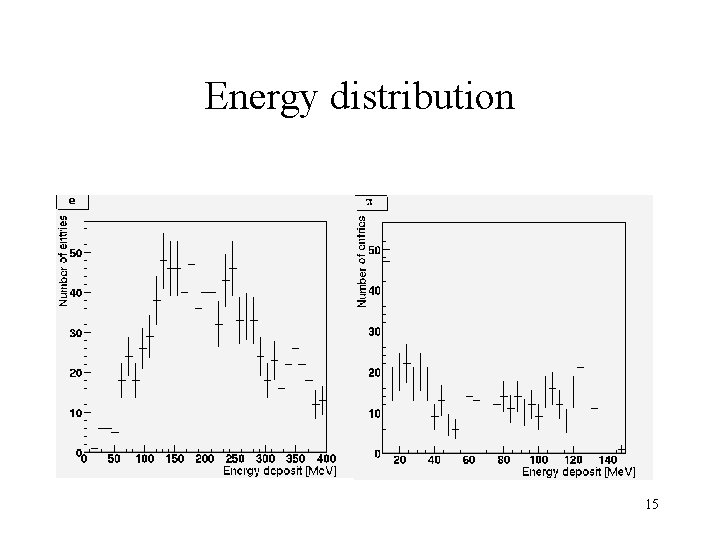
Energy distribution 15

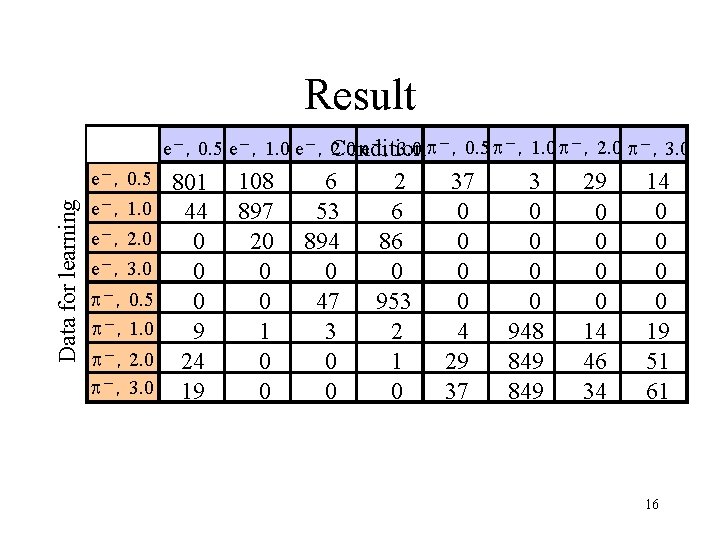
Result Data for learning e－，0. 5 e－，1. 0 e－，2. 0 e－，3. 0 p－，0. 5 p－，1. 0 p－，2. 0 p－，3. 0 Condition e－，0. 5 e－，1. 0 e－，2. 0 e－，3. 0 p－，0. 5 p－，1. 0 p－，2. 0 p－，3. 0 801 44 0 0 0 9 24 19 108 897 20 0 0 1 0 0 6 53 894 0 47 3 0 0 2 6 86 0 953 2 1 0 37 0 0 4 29 37 3 0 0 948 849 29 0 0 14 46 34 14 0 0 19 51 61 16

Summary • We made an attempt to identify particle by means of modeling the shower profile based on Bayesian statistics and develop the possibility for Bayesian approach. • Without any other information e. g. charges of particles given by tracking detectors, we have obtained a high percentage of correct identification for e- and p • Future plan • improvement of model and prior distribution 17