a a 2020 2021 Mobile robots Part I

a. a. 2020 -2021 Mobile robots Part I. 2

Mobile Robots MOBILE ROBOT KINEMATICS

Robot kinematics • Fixed wheels Steerable wheels
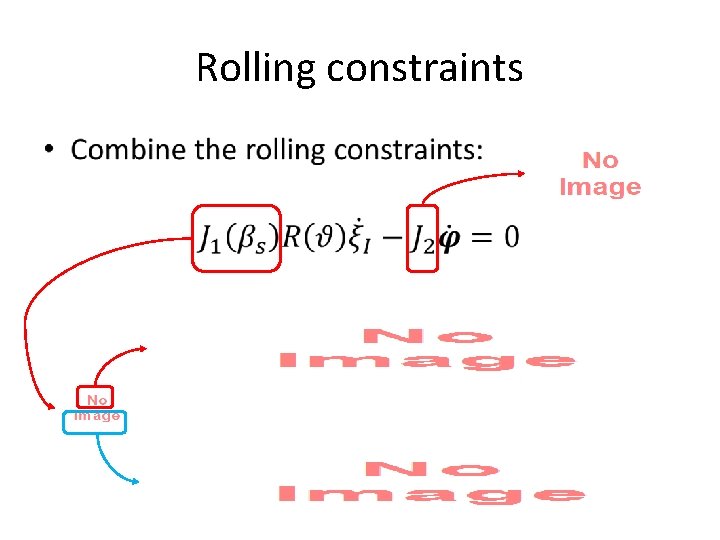
Rolling constraints •

Sliding constraints •

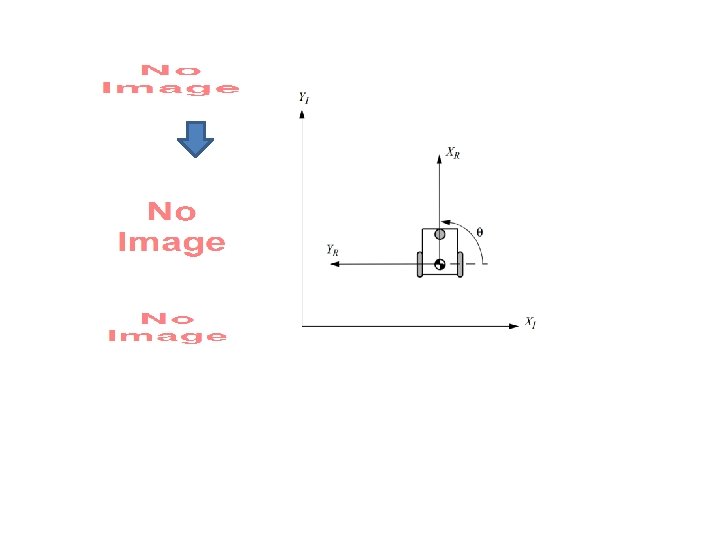
Model • Rolling constraints Sliding constraints


Example: differential drive • Same sliding constraint!
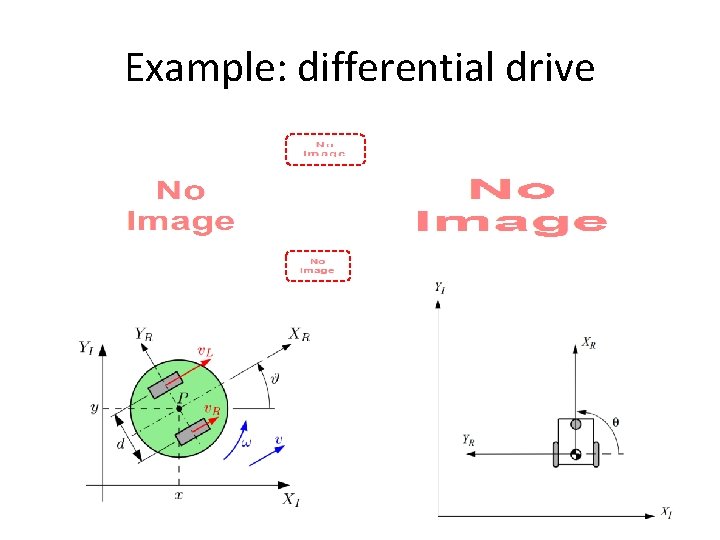
Example: differential drive
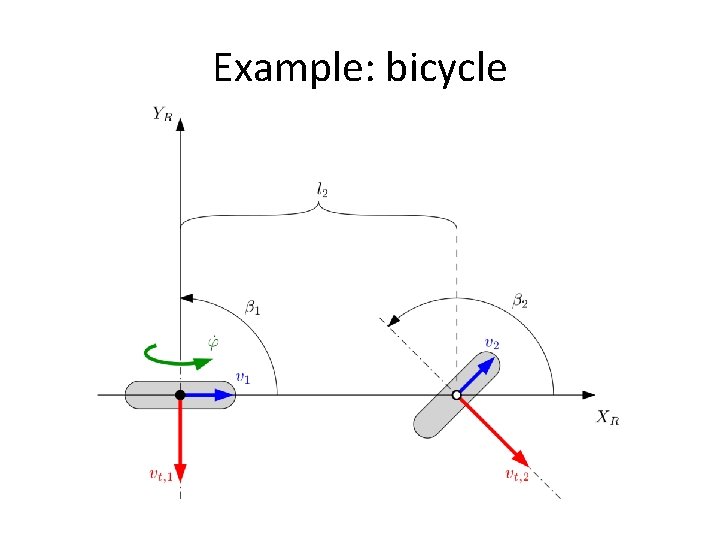
Example: bicycle
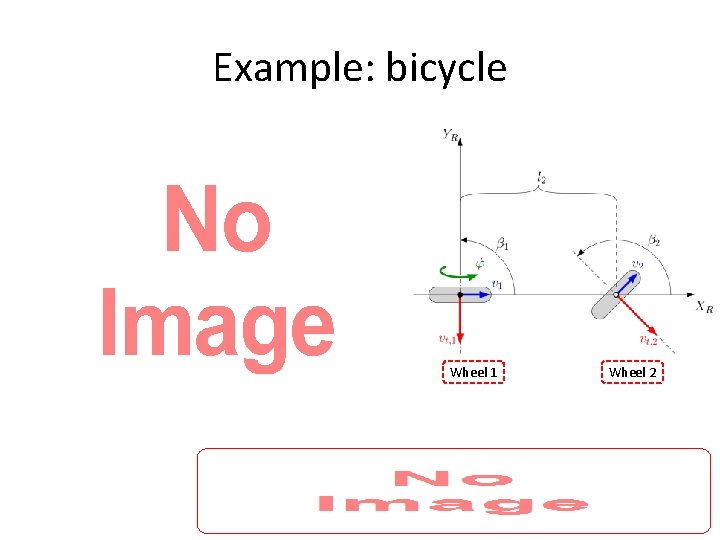
Example: bicycle • Wheel 1 Wheel 2

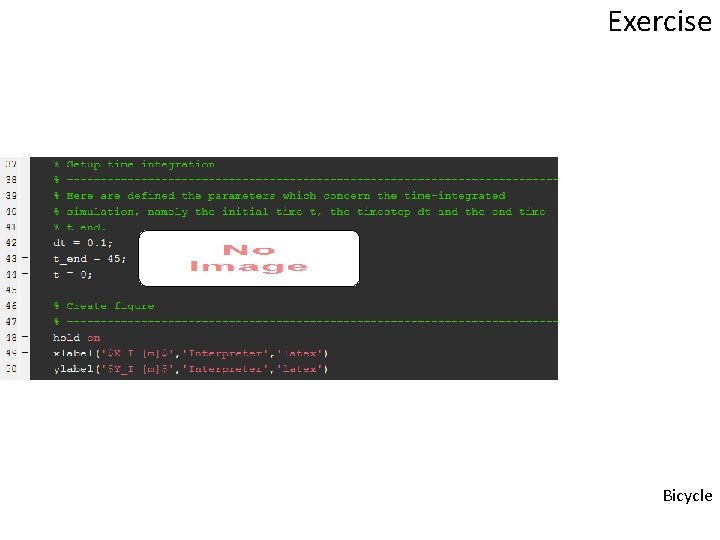
Exercise Bicycle
Exercise Bicycle
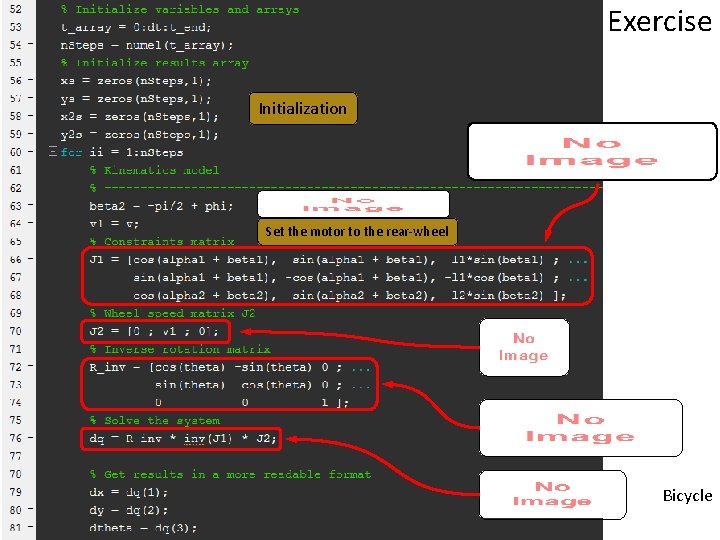
Exercise Initialization Set the motor to the rear-wheel Bicycle
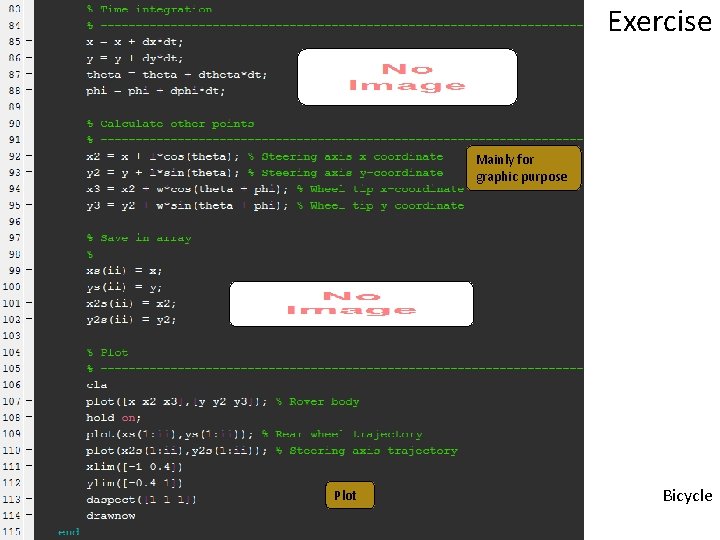
Exercise Mainly for graphic purpose Plot Bicycle
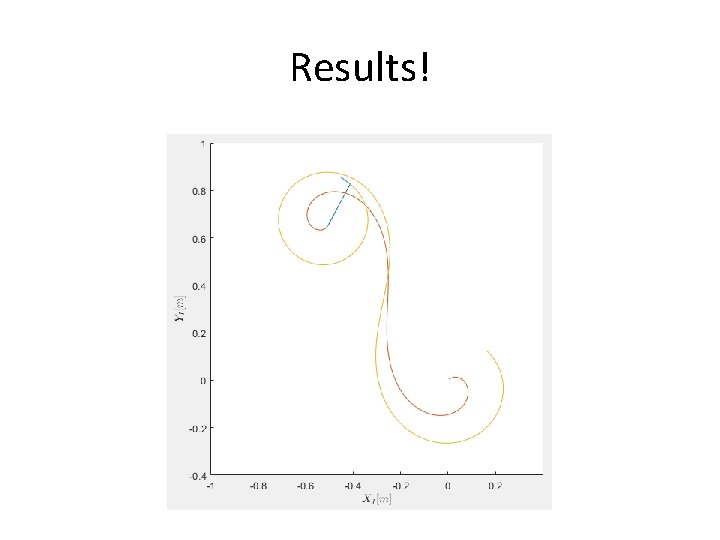
Results!

Mobile robot kinematics EXERCISES

Differential drive robot: forward kinematics exercise_fwd. Kin_diff. Drive. m

Bicycle drive robot: forward kinematics exercise_fwd. Kin_bicycle. m
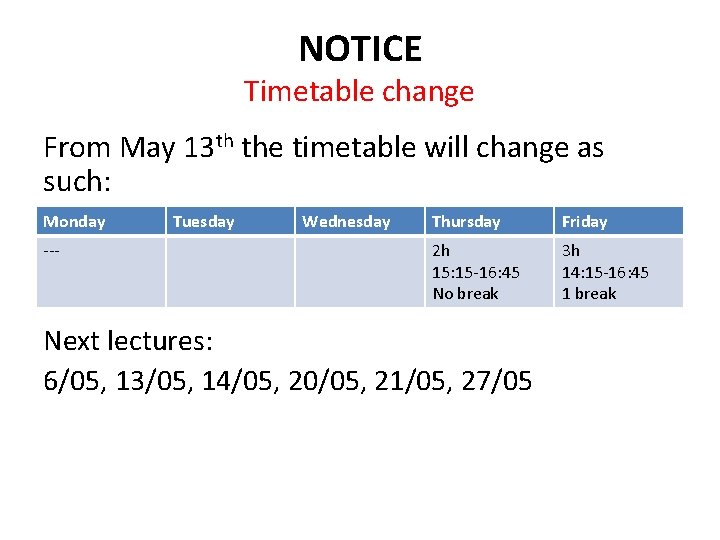
NOTICE Timetable change From May 13 th the timetable will change as such: Monday --- Tuesday Wednesday Thursday Friday 2 h 15: 15 -16: 45 No break 3 h 14: 15 -16: 45 1 break Next lectures: 6/05, 13/05, 14/05, 20/05, 21/05, 27/05

Mobile Robotics MOBILITY

Kinematics: recap • Rolling constraints Sliding constraints Projection matrix
Example
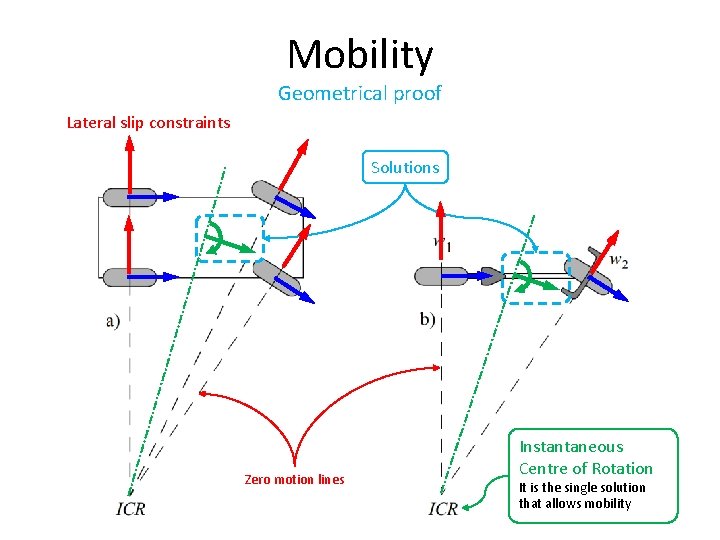
Mobility Geometrical proof Lateral slip constraints Solutions Zero motion lines Instantaneous Centre of Rotation It is the single solution that allows mobility
Rolling constraints Mobility Sliding constraints • Admissible motion vector Motion vector Projection matrix Sliding constraints

Mobility Examples
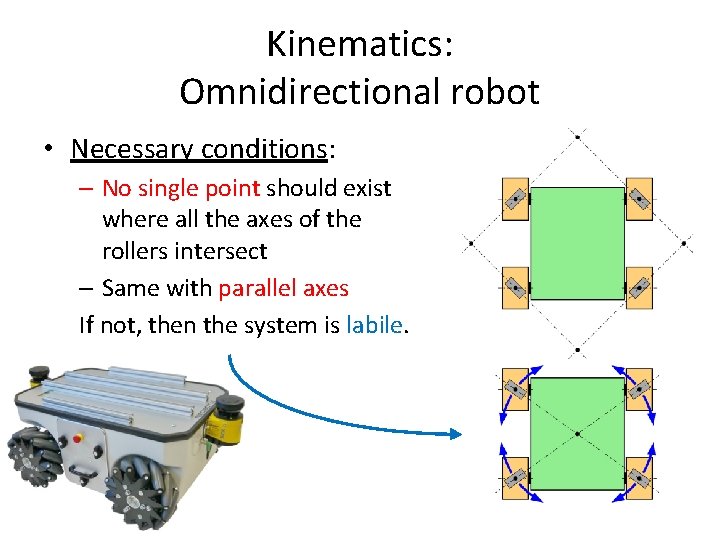
Kinematics: Omnidirectional robot • Necessary conditions: – No single point should exist where all the axes of the rollers intersect – Same with parallel axes If not, then the system is labile.
Mobility • Number of independent constraints Unrestrained motion Unmovable

Steerability • Rolling constraints Sliding constraints
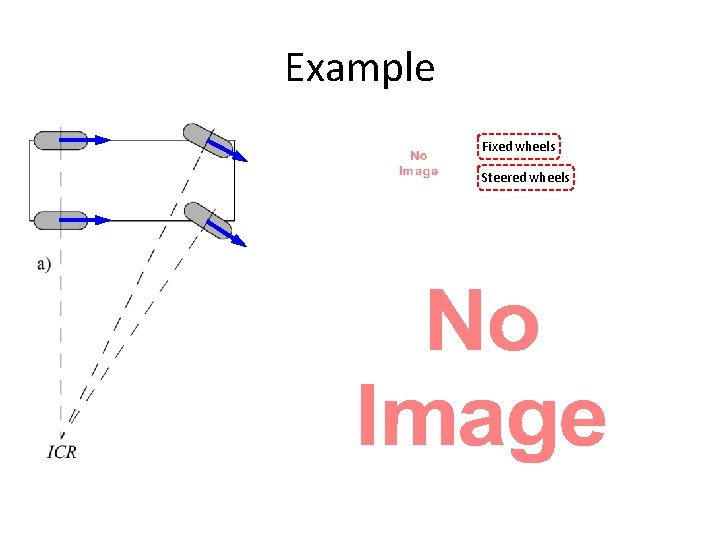
Example Fixed wheels Steered wheels •

Maneuverability •

Mobile robot workspace •
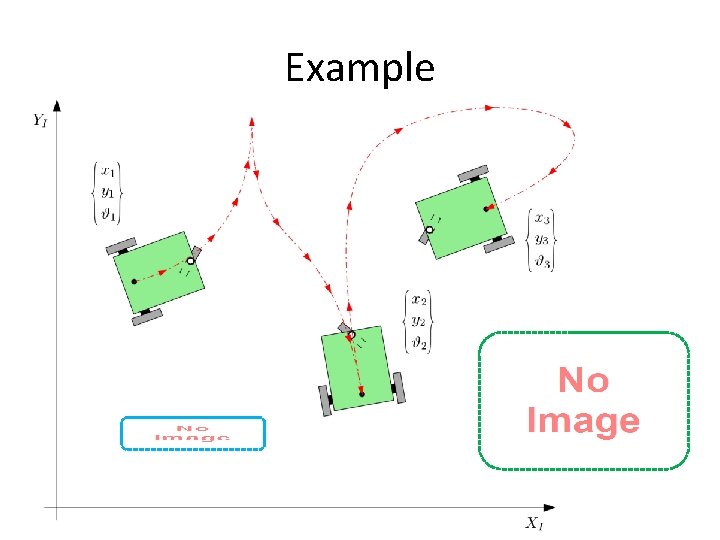
Example
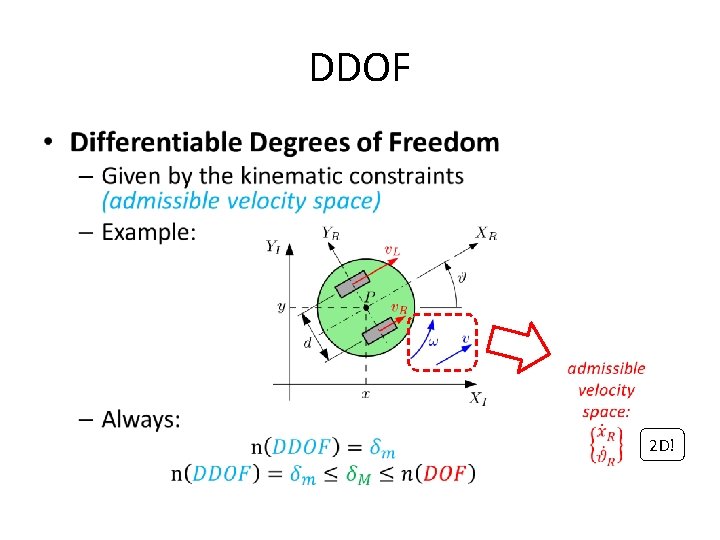
DDOF • 2 D!
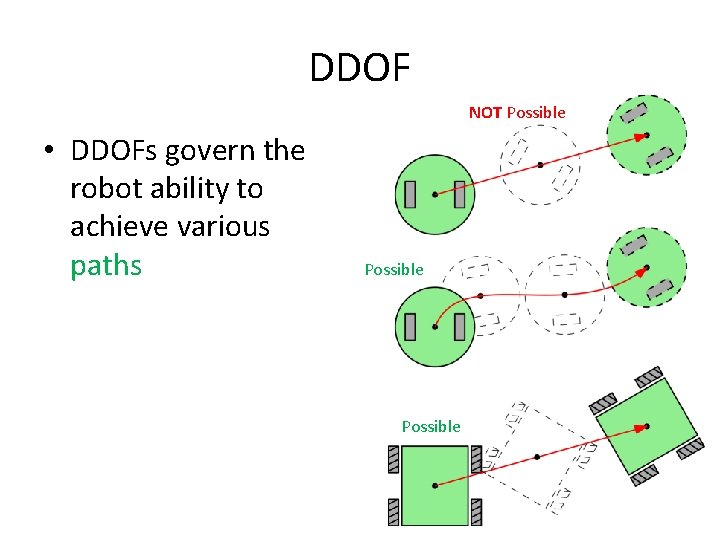
DDOF NOT Possible • DDOFs govern the robot ability to achieve various paths Possible

a. a. 2020 -2021 Robotics Mobile Robots Part I. 07

Mobile Robotics NON-HOLONOMIC CONSTRAINTS

Non-holonomic Constraints •

Non-holonomic Constraints • Any wheeled vehicle is subject to kinematic constraints that reduce in general its local mobility, while leaving intact the possibility of reaching arbitrary configurations by appropriate maneuvers. • Example: – It is impossible to move a car instantaneously in the direction orthogonal to the forward direction. – The same car can perform a S-manoeuver: the result is a displacement in the orthogonal direction!

Holonomic/Non-holonomic constraints • P

Holonomic Constraints •

Non-holonomic Constraints • Dependent both on position and velocity!

Non-holonomic Constraints • Linear! ü Note: the proof of this is a little too involved for us: it revolves around the Frobenius Theorem and Lie brackets theory.

Non-holonomic Constraints To summarize: Non-holonomic constraints are representable only as constraints on velocities and not on positions. Whatever kinematic constraint that is representable as a positional constraint is holonomic.

Non-holonomic Constraints •

Model derivation • or Null-space

Model derivation •
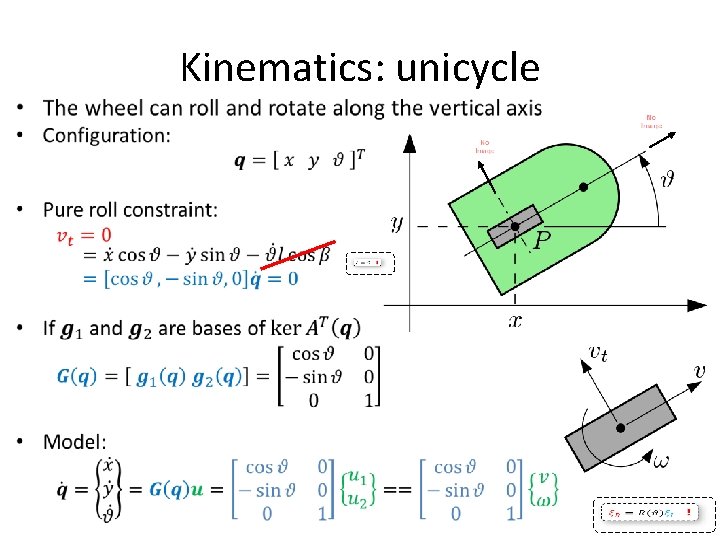
Kinematics: unicycle •

Kinematics: differential steering •

Kinematics: bicycle Part 1 •
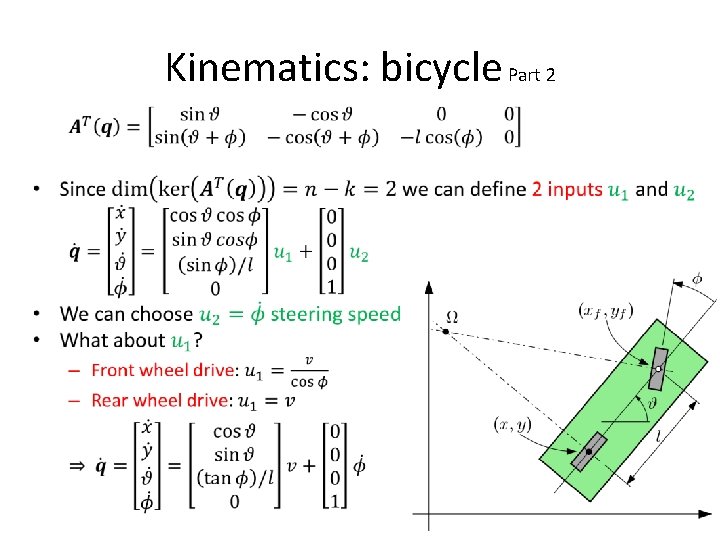
Kinematics: bicycle Part 2 •

Mobile Robotics CONTROL

Control problem •
Control problem •
Precomputed trajectory tracking •
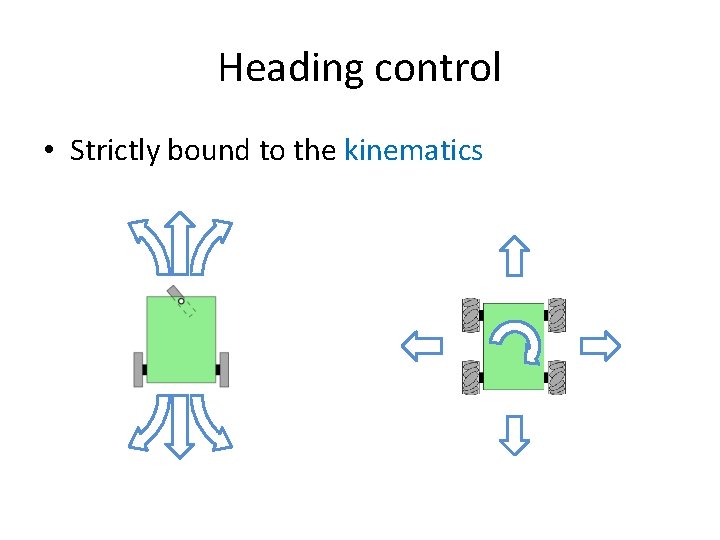
Heading control • Strictly bound to the kinematics

Control basics •
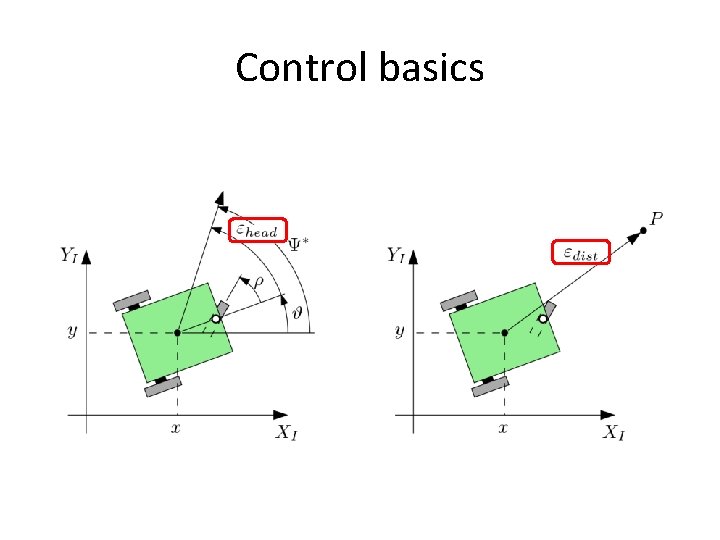
Control basics
Heading control: differential steering Part 1 •

Heading control: differential steering Part 2 • Desired direction
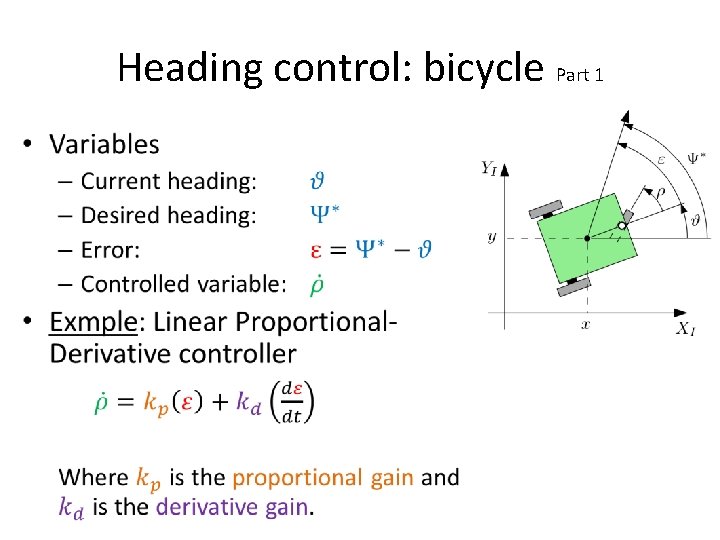
Heading control: bicycle Part 1 •

Forward speed controller •

Heading controller •

Mobile robot control EXERCISES
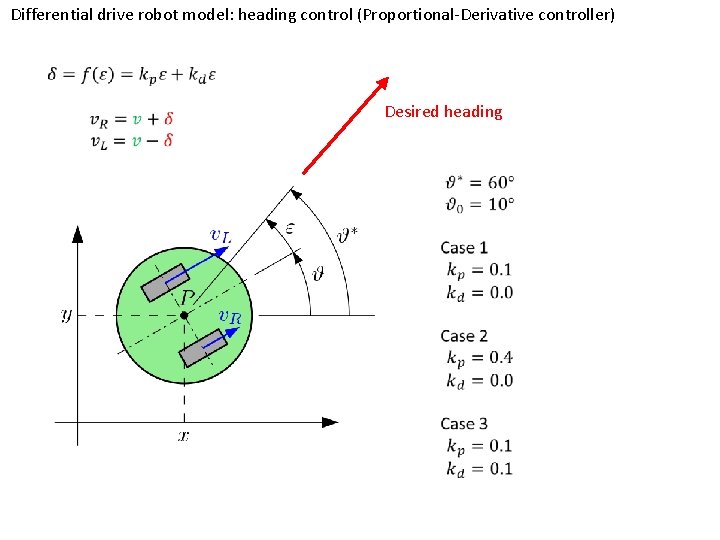
Differential drive robot model: heading control (Proportional-Derivative controller) Desired heading
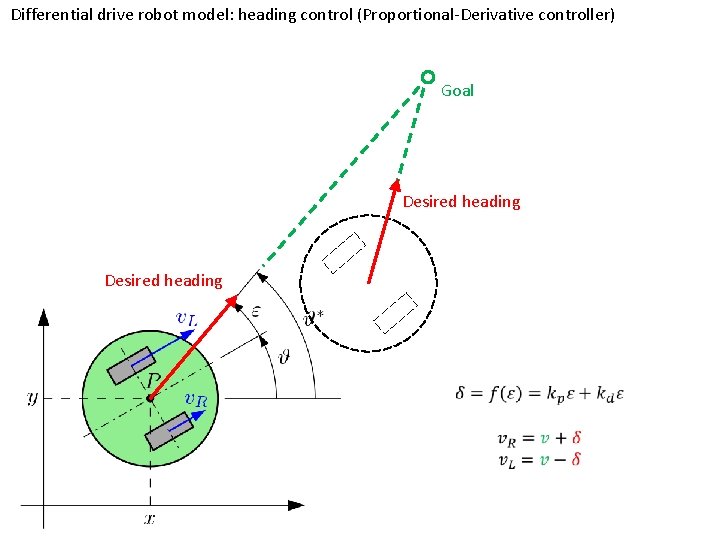
Differential drive robot model: heading control (Proportional-Derivative controller) Goal Desired heading
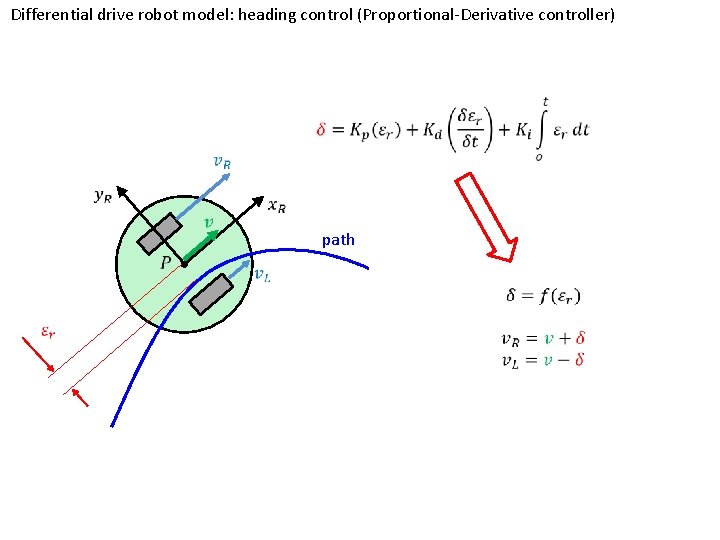
Differential drive robot model: heading control (Proportional-Derivative controller) path
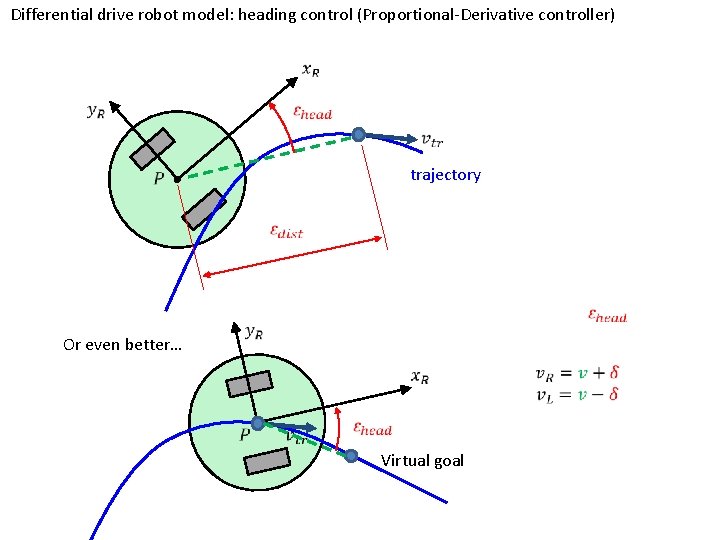
Differential drive robot model: heading control (Proportional-Derivative controller) trajectory Or even better… Virtual goal
- Slides: 69