A 2 Operations Management Critical Path Analysis How

A 2 Operations Management Critical Path Analysis

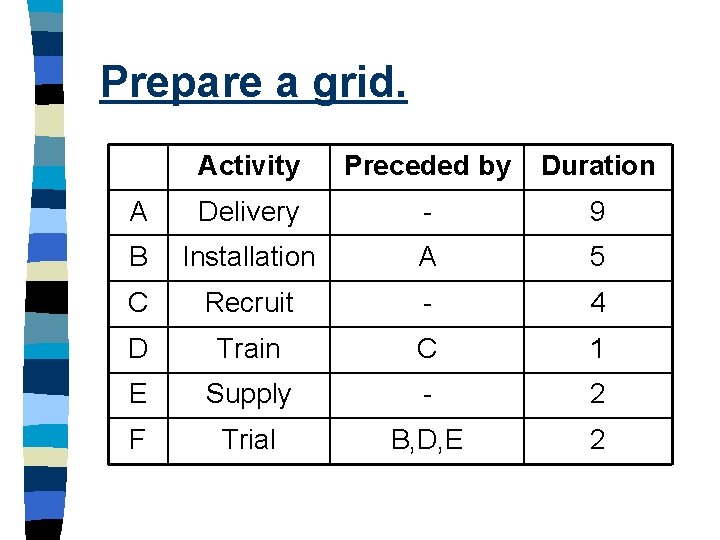
How long will it take? n Walls have decided to launch a new Magnum ice cream. Machine delivery will take 9 weeks, installation takes 5 weeks, staff recruitment 4 weeks and training a further week. Suppliers need 2 weeks lead time and the trial production run will take 2 weeks. n How long until the new magnums will be in the retailers fridges? n Answers? 22 weeks? Longer? Shorter? n n n

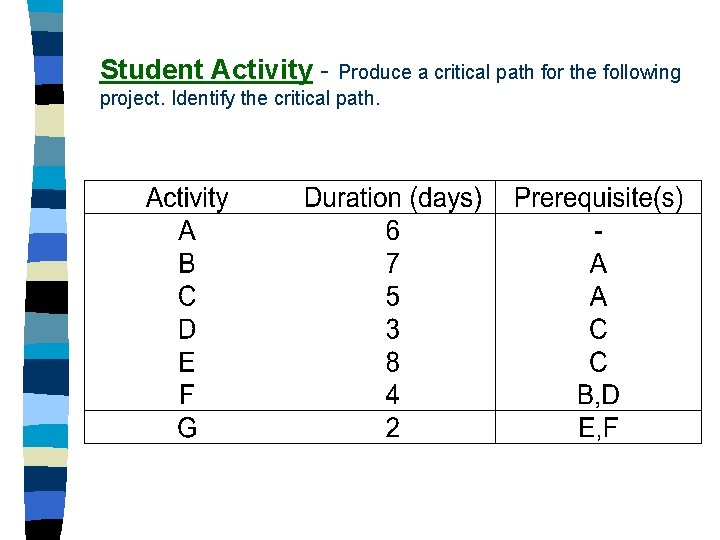
Prepare a grid. Activity Preceded by Duration A Delivery - 9 B Installation A 5 C Recruit - 4 D Train C 1 E Supply - 2 F Trial B, D, E 2

Answer

Critical Path Analysis n The process of planning the sequence of activities in a project in order to discover the most efficient and quickest way of completing it. n Widely used in industries such as construction where it is possible to operate a range of activities in parallel n By mapping out the network of different activities firms can see which activities can be run at the same time n It also allows firms to see which activities can not be delayed without holding up the overall project

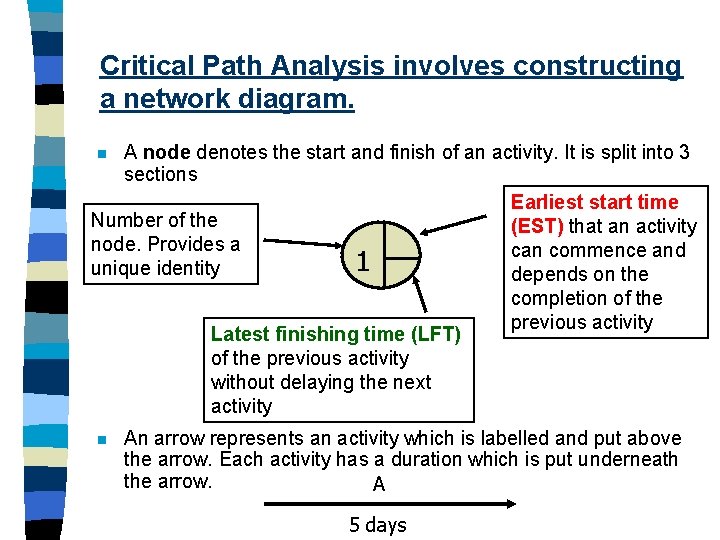
Critical Path Analysis involves constructing a network diagram. A node denotes the start and finish of an activity. It is split into 3 sections Earliest start time Number of the (EST) that an activity node. Provides a can commence and 1 unique identity depends on the completion of the previous activity Latest finishing time (LFT) of the previous activity without delaying the next activity n n An arrow represents an activity which is labelled and put above the arrow. Each activity has a duration which is put underneath the arrow. A 5 days

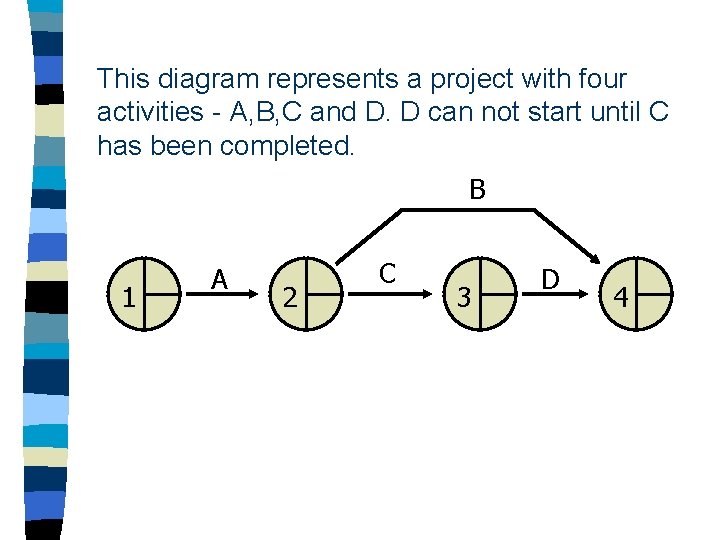
This diagram represents a project with four activities - A, B, C and D. D can not start until C has been completed. B 1 A 2 C 3 D 4

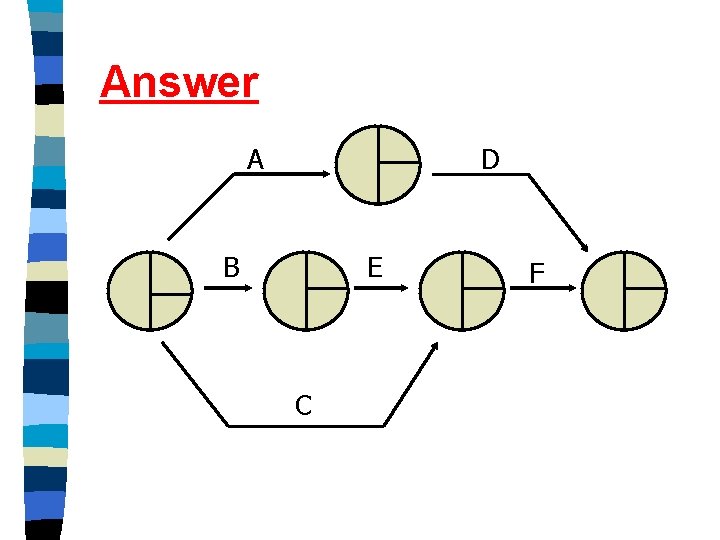
Student activity n Draw a network using the following information: A, B and C begin together. D follows A, E follows B, F follows C and E.

Answer A D B E C F

Constructing a critical path network n Prerequisite - the activity that must be completed before our selected activity can occur. E. g. digging foundations for a house before building the walls

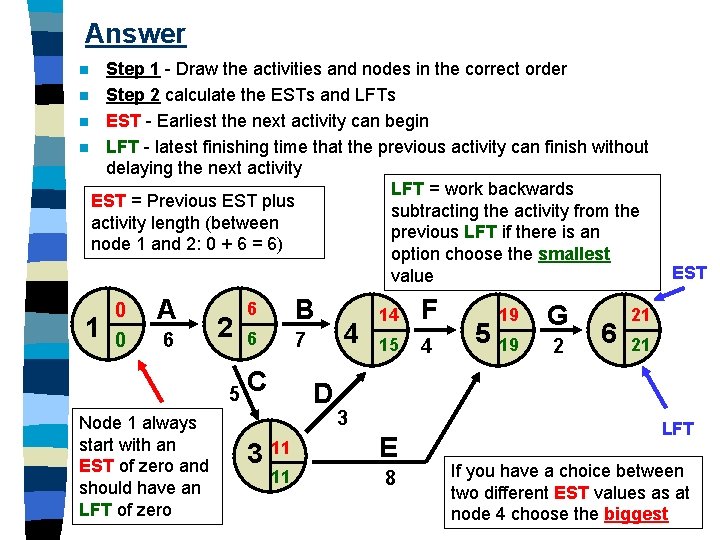
Constructing a critical path network n Step 1: Draw a node to represent the start of the network. All networks must start and end with a node. Do not draw a node at the end of an activity line immediately, ensure it is right first. A node represents the point at which a new activity can begin. n Step 2: Identify activities with no prerequisites. Draw lines from left to right from node 1. n Step 3: Label activity lines with description and duration n Step 4: Move onto the first activity with a prerequisite. Place a node at the end of the line and draw the next activity which is reliant on the previous activity being completed. n Step 5: Repeat steps 3 and 4 until complete. Then calculate the ESTs and LFTs. Then the critical path can be established.

Constructing the Critical Path Analysis n Earliest starting time (EST) - Move forward through the nodes and always pick the largest of the options. Work right choosing the highest option for each node. n Latest finishing time (LFT) - move back from the final node and always pick the smallest of the options. Work left choosing the lowest option for each node.

The Critical Path n The sequence of activities that cannot be delayed without delaying the overall completion of the project. n It is represented by activities that have identical LFTs and ESTs and it is the longest path between nodes.

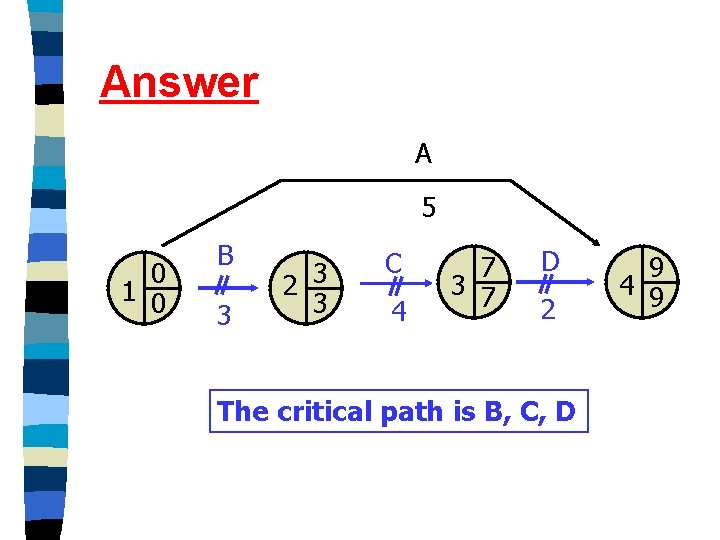
Student activity - Complete the critical path analysis for the following project. Identify the critical path.

Answer A 5 0 1 0 B 3 2 3 3 C 4 7 3 7 D 2 The critical path is B, C, D 9 4 9

Tips n Always ask your self the question: What activity can I do next? n A node is like a full stop. It must go at the end of an activity, it does not represent an activity

Critical path analysis - Lesson 2 - Recap n Critical path analysis is a way of showing how a lengthy and complex project (e. g. a building project, marketing campaign) can be completed in the shortest possible time. n It shows which of the activities are ‘critical’ - this means that if these activities are delayed, then the project will not be able to be completed on time.

Student Activity - Produce a critical path for the following project. Identify the critical path.

Answer Step 1 - Draw the activities and nodes in the correct order n Step 2 calculate the ESTs and LFTs n EST - Earliest the next activity can begin n LFT - latest finishing time that the previous activity can finish without delaying the next activity LFT = work backwards EST = Previous EST plus subtracting the activity from the activity length (between previous LFT if there is an node 1 and 2: 0 + 6 = 6) option choose the smallest value n 1 0 0 A 6 2 5 Node 1 always start with an EST of zero and should have an LFT of zero 6 B 6 7 C 3 D 4 14 F 15 4 3 11 E 11 8 5 19 G 19 2 6 EST 21 21 LFT If you have a choice between two different EST values as at node 4 choose the biggest

Step 3 - Label the Critical Path n The critical path is the sequence of activities that cannot be delayed without delaying the overall project completion. n It is represented by the activities with identical ESTs and LFTs and the longest path between the nodes n The critical path for the previous example would be: Critical path A, C, E, G n n On the diagram the critical path activities will be symbolised with two lines through the activity line

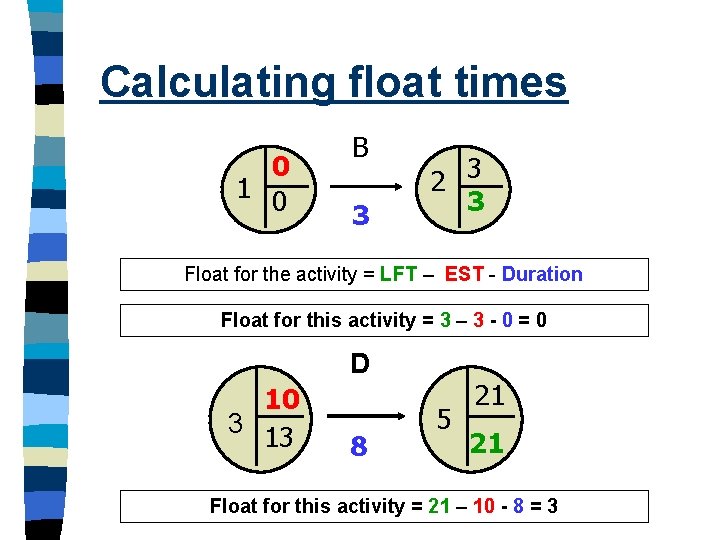
Float Times n Float time - the amount of time that non-critical activities within a project can be delayed without affecting the deadline for completion of the whole project. n Total float for an activity- the amount of time an activity can be delayed without delaying the whole project n Total Float for an activity= LFT -EST - duration of the activity n E. g. Activity D = 15 - 11 - 3 = 1 day n Therefore the activity may be delayed by 1 day without affecting the whole project

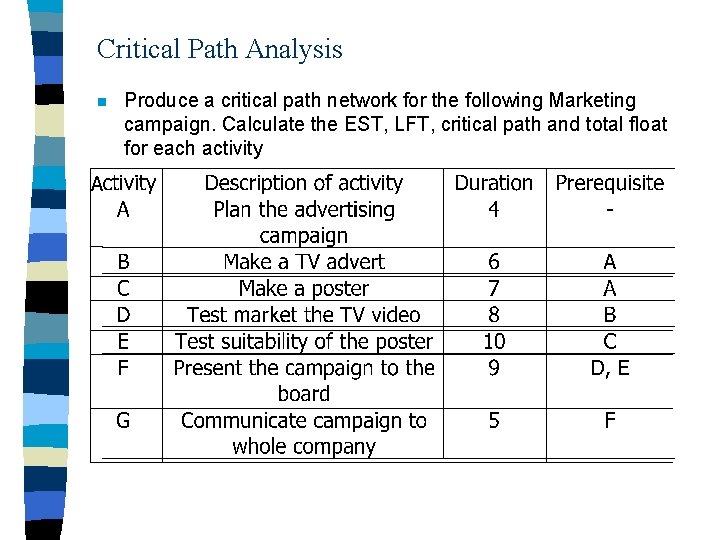
Critical Path Analysis n A Produce a critical path network for the following Marketing campaign. Calculate the EST, LFT, critical path and total float for each activity

Calculating float times 0 1 0 B 3 2 3 3 Float for the activity = LFT – EST - Duration Float for this activity = 3 – 3 - 0 = 0 D 10 3 13 8 5 21 21 Float for this activity = 21 – 10 - 8 = 3

Float times for Marketing strategy activity n A=4 -0 -4=0 n B = 13 – 4 – 6 = 3 n C = 11 – 7 – 4 = 0 n D = 21 – 13 – 8 = 0 n E = 21 – 10 = 0 n F = 30 – 21 – 9 = 0 n G = 35 – 30 – 5 = 0

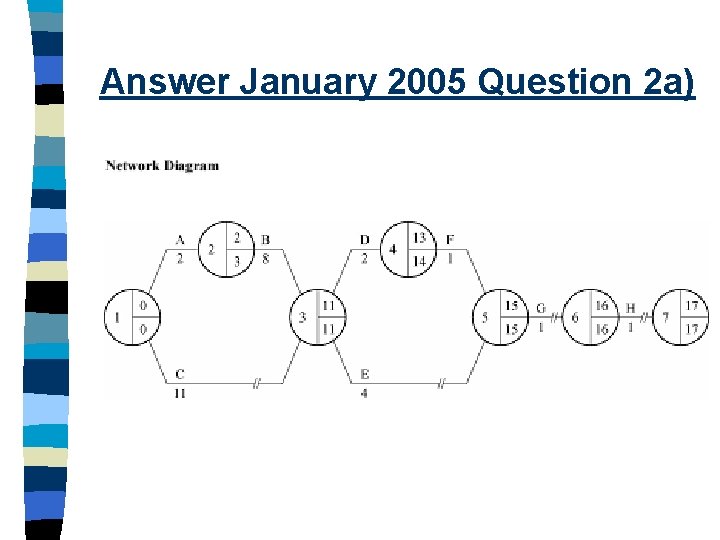
Student Activity n Complete the exam question 2 a) for January 2005 Unit 4 exam paper

Answer January 2005 Question 2 a)

Problems of using CPA n Can encourage rigidity n If every activity is strictly time-tabled a delay in a critical activity may result in a greater overall delay n CPA focuses on speed of completion rather than quality n CPA relies on estimated completion times n Complex projects may be difficult to produce n Sub-contractors are outside of the firms control and may not stick to deadlines n Supplies may be delayed

Business Implications of Critical Path Analysis 1. Read and highlight the information on the business implications of using CPA 2. Complete questions 1 and 2 on the information sheet n For both critical path questions calculate all ESTs, LFTs, the critical path and the float time of each activity