A 1 Sequences 1 What is a sequence




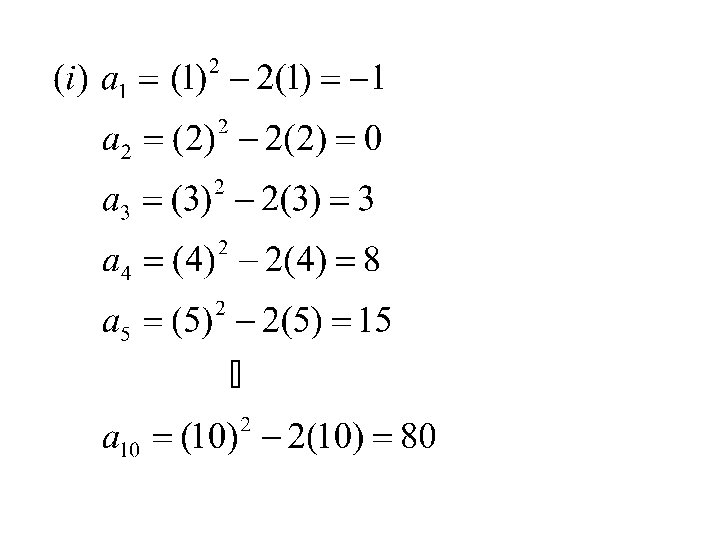

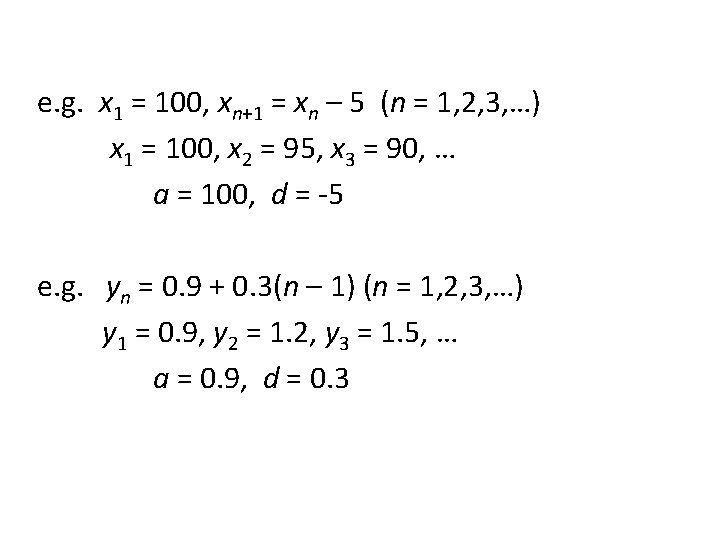



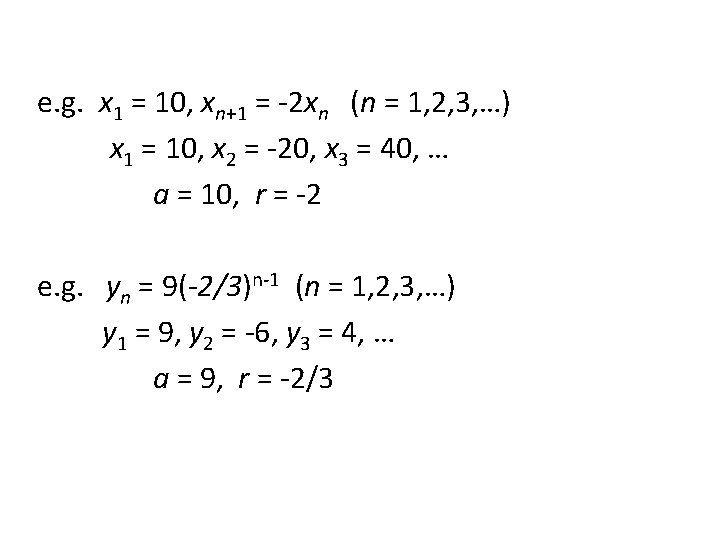



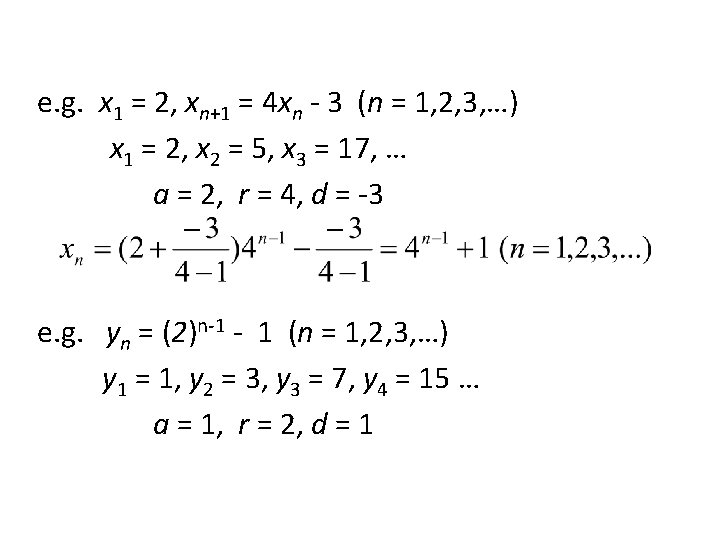


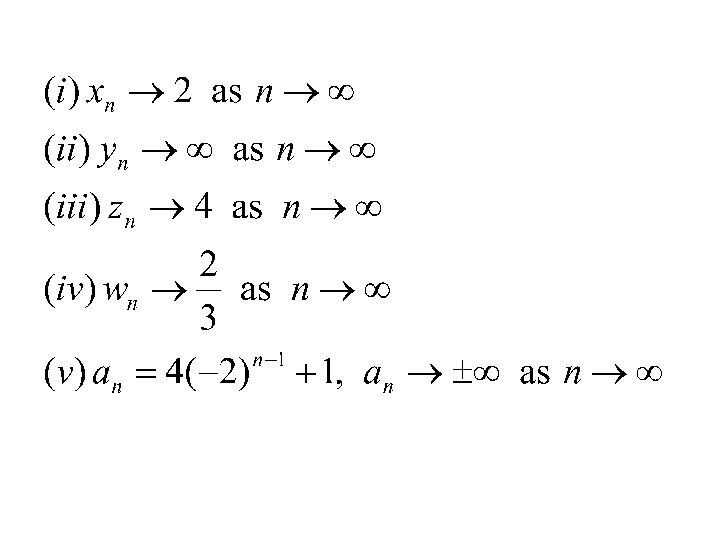


- Slides: 24

A 1. Sequences 1. What is a sequence? 2. Arithmetic sequences 3. Geometric sequences 4. Linear recurrence sequences 5. Long-term behavior of sequences 6. Sequences and modeling 7. Sum of geometric series

1. What is a sequence? Definition: A sequence in a discrete structure is used to represent an ordered list. Or 1, 2, 3, … Function

• Infinite sequences: a 1 = 4, a 2 = 7, a 3 = 10, a 4 = 13, … b 1 = 1/4, b 2 = -1/8, b 3 = 1/16, b 4 = -1/32, … 1, 1, 2, 3, 5, 8, 13, 21, … • Finite sequences: 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1 9, -6, 4, -8/3, 16/9, -32/27 In general,

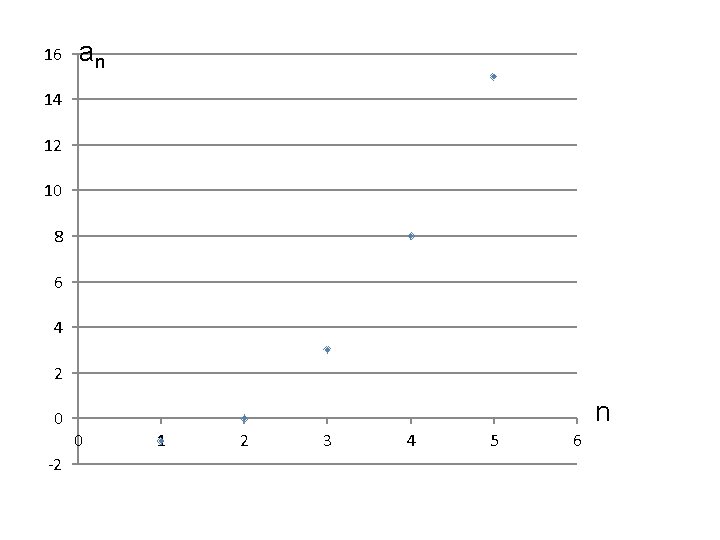
Example: For each of the following sequences write down the first 5 terms, the 10 th term, and plot a graph showing the first 5 terms:
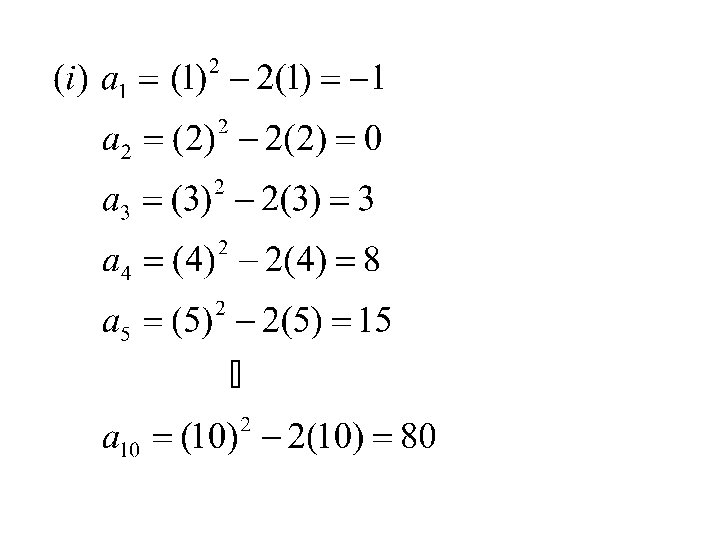

16 an 14 12 10 8 6 4 2 0 -2 n 0 1 2 3 4 5 6

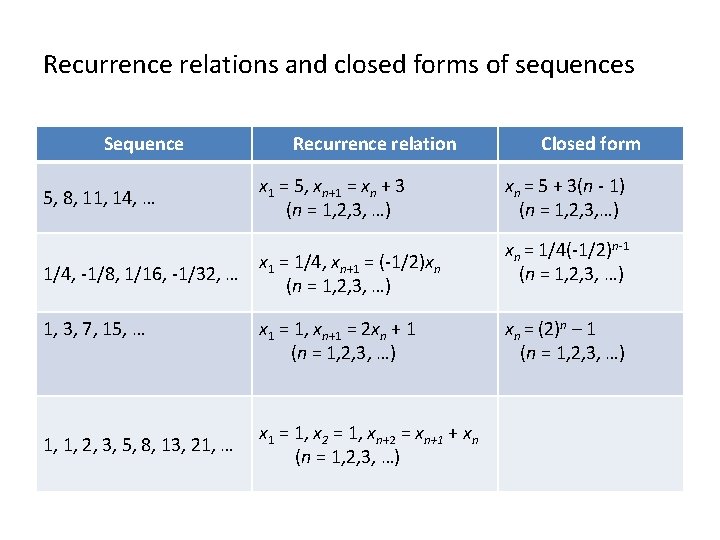
Recurrence relations and closed forms of sequences Sequence 5, 8, 11, 14, … 1/4, -1/8, 1/16, -1/32, … 1, 3, 7, 15, … 1, 1, 2, 3, 5, 8, 13, 21, … Recurrence relation x 1 = 5, xn+1 = xn + 3 (n = 1, 2, 3, …) x 1 = 1/4, xn+1 = (-1/2)xn (n = 1, 2, 3, …) x 1 = 1, xn+1 = 2 xn + 1 (n = 1, 2, 3, …) x 1 = 1, x 2 = 1, xn+2 = xn+1 + xn (n = 1, 2, 3, …) Closed form xn = 5 + 3(n - 1) (n = 1, 2, 3, …) xn = 1/4(-1/2)n-1 (n = 1, 2, 3, …) xn = (2)n – 1 (n = 1, 2, 3, …)

2. Arithmetic sequences A sequence of either of the forms x 1 = a, xn+1 = xn + d (n = 1, 2, 3, …) or xn = a + (n – 1)d (n = 1, 2, 3, …) is called arithmetic sequence with parameters a, the first term, and d, the common differences. +d +d a a+d x 1 x 2 +d a+2 d a+3 d x 3 x 4 …
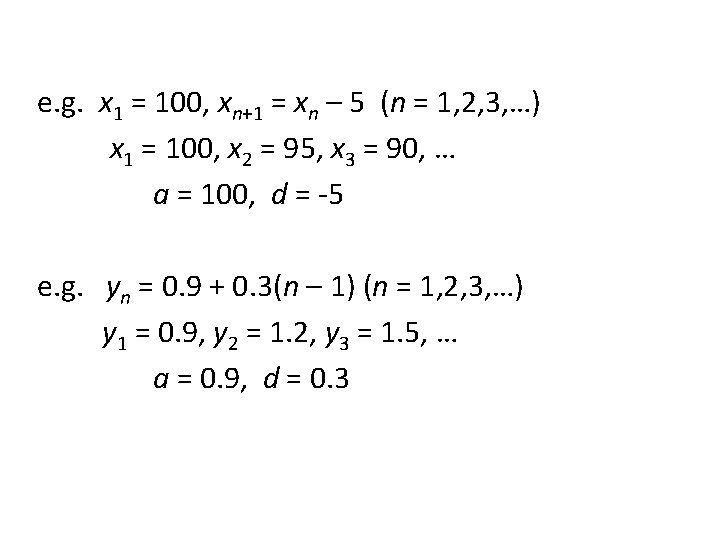
e. g. x 1 = 100, xn+1 = xn – 5 (n = 1, 2, 3, …) x 1 = 100, x 2 = 95, x 3 = 90, … a = 100, d = -5 e. g. yn = 0. 9 + 0. 3(n – 1) (n = 1, 2, 3, …) y 1 = 0. 9, y 2 = 1. 2, y 3 = 1. 5, … a = 0. 9, d = 0. 3

Example: For each of the following (arithmetic) sequences obtain the recurrence relation and the closed form:

Example: let {xn}, n =1, 2, 3, … be an arithmetic sequence such that the sum of the 3 rd term and the 5 th term is 16, and the difference between the 7 th term and the 4 th term is 9. Obtain the recurrence relation and the closed form of the sequence.

3. Geometric sequences A sequence of either of the forms x 1 = a, xn+1 = rxn (n = 1, 2, 3, …) or xn = arn-1 (n = 1, 2, 3, …) is called geometric sequence with parameters a, the first term, and r, the common ratio. *r *r *r a ar ar 2 ar 3 x 1 x 2 x 3 x 4 …
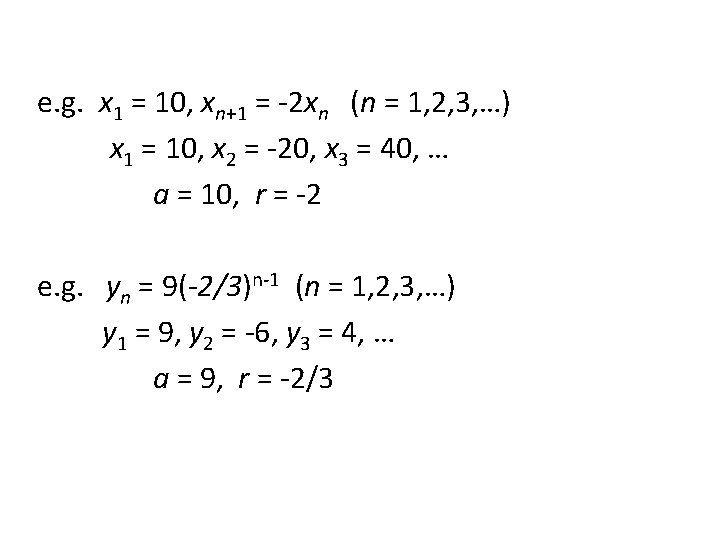
e. g. x 1 = 10, xn+1 = -2 xn (n = 1, 2, 3, …) x 1 = 10, x 2 = -20, x 3 = 40, … a = 10, r = -2 e. g. yn = 9(-2/3)n-1 (n = 1, 2, 3, …) y 1 = 9, y 2 = -6, y 3 = 4, … a = 9, r = -2/3

Example: For each of the following (geometric) sequences obtain the recurrence relation and the closed form:

Example: let {yn}, n =1, 2, 3, … be a geometric sequence whose 4 th term is -1/80 and 7 th term is 1/640. Obtain the recurrence relation and the closed form of the sequence.

4. Linear recurrence sequences A sequence of the form x 1 = a, xn+1 = rxn + d (n = 1, 2, 3, …) is called linear recurrence sequence with parameters a, r and d. a ra+d r(ra+d)+d a(r 2 a+rd+d)+d x 1 x 2 x 3 x 4 … Note: 1) 2) If r = 1, we have arithmetic sequence. 3) If d = 0, we have geometric sequence.
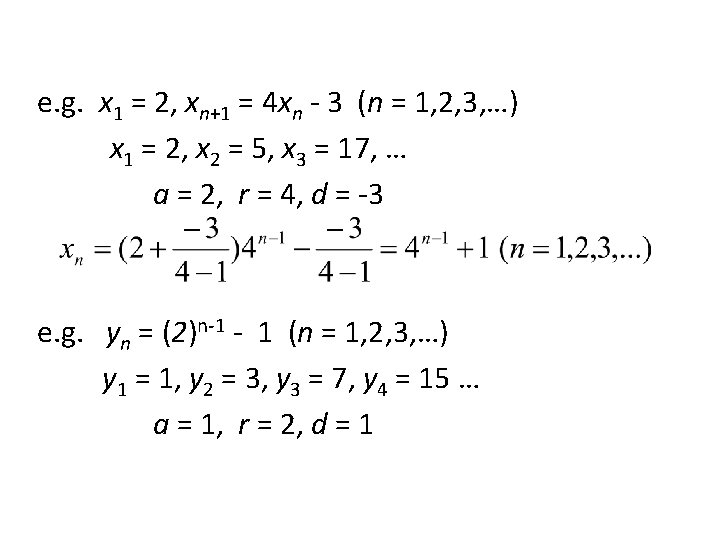

Example: Find the recurrence relation and the closed form for following the linear recurrence sequence: 2, -7, 11, -23….

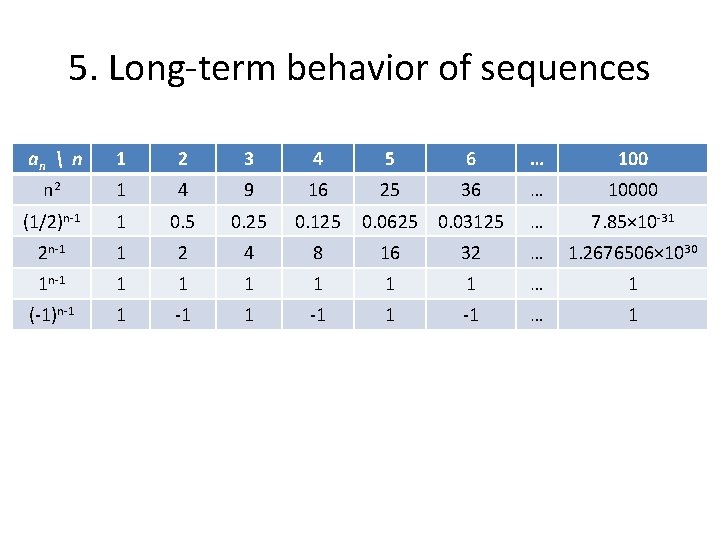
5. Long-term behavior of sequences an n 1 2 3 4 5 6 … 100 n 2 1 4 9 16 25 36 … 10000 (1/2)n-1 1 0. 5 0. 25 0. 125 0. 0625 0. 03125 … 7. 85× 10 -31 2 n-1 1 2 4 8 16 32 … 1. 2676506× 1030 1 n-1 1 1 1 … 1 (-1)n-1 1 -1 … 1

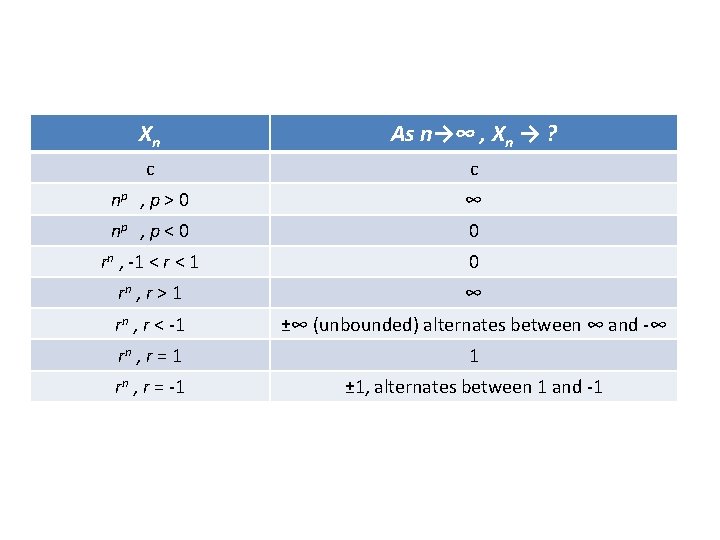
Xn As n→∞ , Xn → ? c c np , p > 0 ∞ np , p < 0 0 rn , -1 < r < 1 0 rn , r > 1 ∞ rn , r < -1 ±∞ (unbounded) alternates between ∞ and -∞ rn , r = 1 1 rn , r = -1 ± 1, alternates between 1 and -1

Example: Describe the long-term behavior of the following sequences:
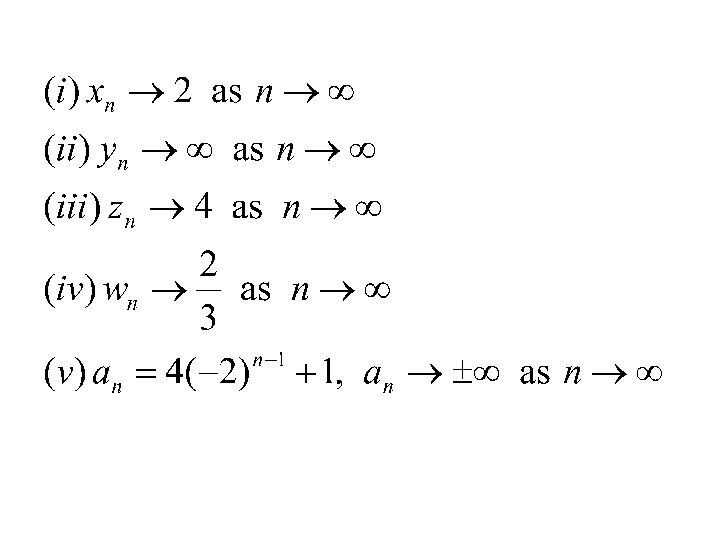

6. Sequences and modeling • The saving account sequence: b 1 = 5000, bn+1 = 1. 06 bn (n = 1, 2, 3, …) • The population sequence: p 1 = 50, 000, pn+1 = 1. 12 pn – 1000 (n = 1, 2, 3, …) • The bouncing ball sequence: h 1 = 10, hn+1 = 0. 75 hn (n = 1, 2, 3, …)

7. Sum of geometric series A 2