The Quadratic Equation x b b 4 ac

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a Standard form of a quadratic equation is ax² + bx + c = 0 iff a ≠ 0, where a, b, and c are real numbers, b and/or c can be equal zero a is the coefficient of the x² term b is the coefficient of the x term c is the constant (the number without a variable) the coefficient is the number, sign included in front of the variable

How to Solve a Quadratic Equation J Make sure your equation is in Standard Form. every term to the LHS J Find the values of a, b, and c. a= , b= , c= J Does the parabola open up or down?

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a This is a “plug and chug” problem. Just follow the steps. You plug in the numbers for the variables and do the operations. Let’s try this one a= b= c= x² - 8 x + 15 = 0

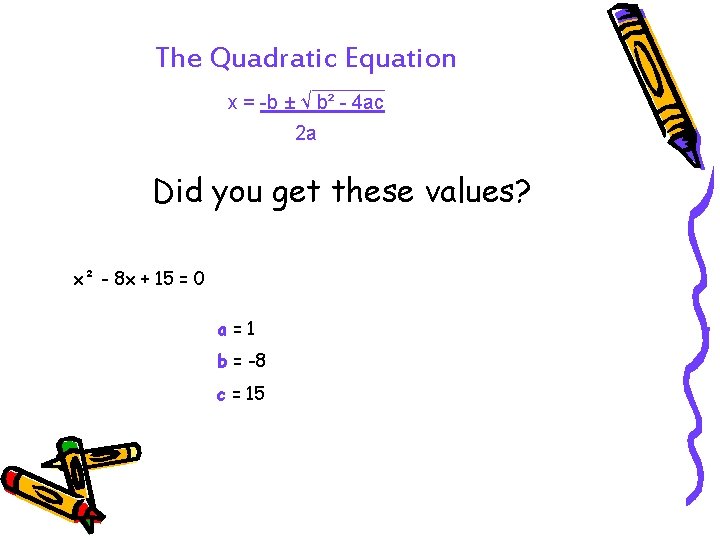
The Quadratic Equation x = -b ± √ b² - 4 ac 2 a Did you get these values? x² - 8 x + 15 = 0 a=1 b = -8 c = 15

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a Next step is to find the axis of symmetry. this is the vertical line that “cuts” the parabola into two symmetrical halves x² - 8 x + 15 = 0 a=1 Use this to find the axis of symmetry b = -8 x= -b c = 15 2 a

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a This is another “plug and chug” problem. You plug in the numbers for the variables and do the operations. x² - 8 x + 15 = 0 Did you find the axis of symmetry? x= -b 2 a x = - (-8) 2(1) x=8 2 or x = 4 when simplified

How to Solve a Quadratic Equation J Make sure your equation is in Standard Form. J Find the values of a, b, and c. J Does the parabola open up or down? J Calculate the axis of symmetry.

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a x² - 8 x + 15 = 0 The axis of symmetry is x = 4 Now we have to find the coordinates of the vertex. We already know the x coordinate from the axis of symmetry. Using the corresponding equation y = x² - 8 x + 15 This is another “plug and chug” problem. You plug in the found value of x into the original equation and do the operations to solve for y.

Ugh … are you having fun yet? I love this stuff!

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a You plug in the found value of x into the original equation and do the operations to solve for y. x=4 y = x² - 8 x + 15 y = (4)² - 8(4) + 15 y = 16 - 32 + 15 y = - 16 + 15 y=-1 The coordinate of our vertex is (4, -1)

How to Solve a Quadratic Equation J Make sure your equation is in Standard Form. J Find the values of a, b, and c. J Does the parabola open up or down? J Calculate the axis of symmetry. J Plug that value back into the original equation to find the coordinates of the vertex. J Draw the axis of symmetry. J Plot and label the vertex.

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a Next is to find where the roots are. That means where the “arms” of the parabola hit the x–axis. x² - 8 x + 15 = 0 a=1 plug and chug these values into the above equation b = -8 -b ± √ b² - 4 ac c = 15 2 a

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a x² - 8 x + 15 = 0 a=1 b = -8 plug and chug the values into the above equation -(-8) ± √ (-8)² - 4(1)(15) 2(1) c = 15 8 ± √ (64) - 60 2 8 ± √ 4 2 this leads us to 2 separate equations 8 ± 2 2

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a Breaking this into the two equations We get 8+2 2 8 -2 2 10 2 5 6. 2 and 3 8± 2 2

How to Solve a Quadratic Equation J Make sure your equation is in Standard Form. J Find the values of a, b, and c. J Does the parabola open up or down? J Calculate the axis of symmetry. J Plug that value back into the original equation to find the coordinates of the vertex. J Calculate the “roots” of the parabola using the quadratic equation. J Draw the axis of symmetry. J Plot and label the vertex. J Plot the roots. J Draw and label the parabola.

The Quadratic Equation x = -b ± √ b² - 4 ac 2 a Let’s try this one a= b= c= x² + 3 x + 2 = 0

How to Solve a Quadratic Equation J Make sure your equation is in Standard Form. J Find the values of a, b, and c. J Does the parabola open up or down? J Calculate the axis of symmetry. J Plug that value back into the original equation to find the coordinates of the vertex. J Calculate the “roots” of the parabola using the quadratic equation. J Draw the axis of symmetry. J Plot and label the vertex. J Plot the roots. J Draw and label the parabola.