9 Systems of Particles 1 2 3 4

9. Systems of Particles 1. 2. 3. 4. 5. 6. Center of Mass Momentum Kinetic Energy of a System Collisions Totally Inelastic Collisions Elastic Collisions

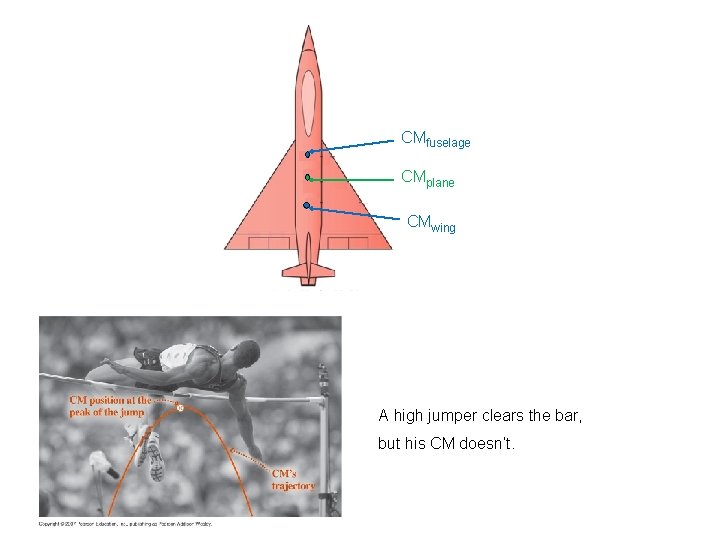
As the skier flies through the air, most parts of his body follow complex trajectories. But one special point follows a parabola. What’s that point, and why is it special? Ans. His center of mass (CM) Rigid body: Relative particle positions fixed.

9. 1. Center of Mass N particles: = total mass = Center of mass = mass-weighted average position with 3 rd law Cartesian coordinates: Extension: “particle” i may stand for an extended object with cm at ri.

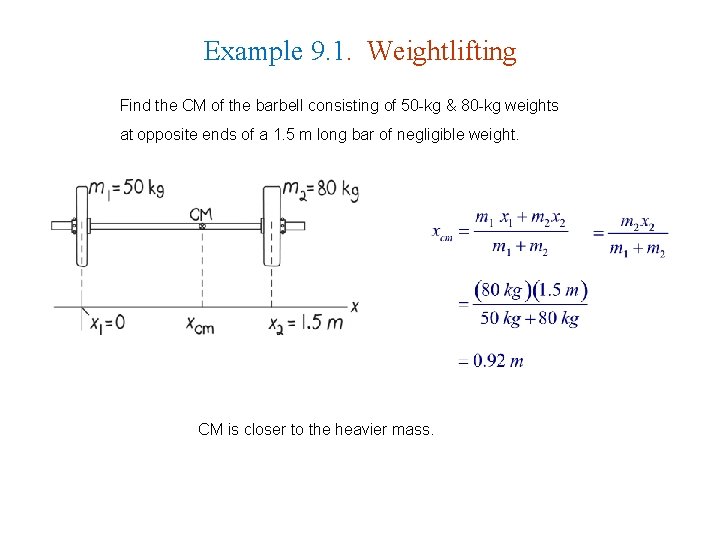
Example 9. 1. Weightlifting Find the CM of the barbell consisting of 50 -kg & 80 -kg weights at opposite ends of a 1. 5 m long bar of negligible weight. CM is closer to the heavier mass.

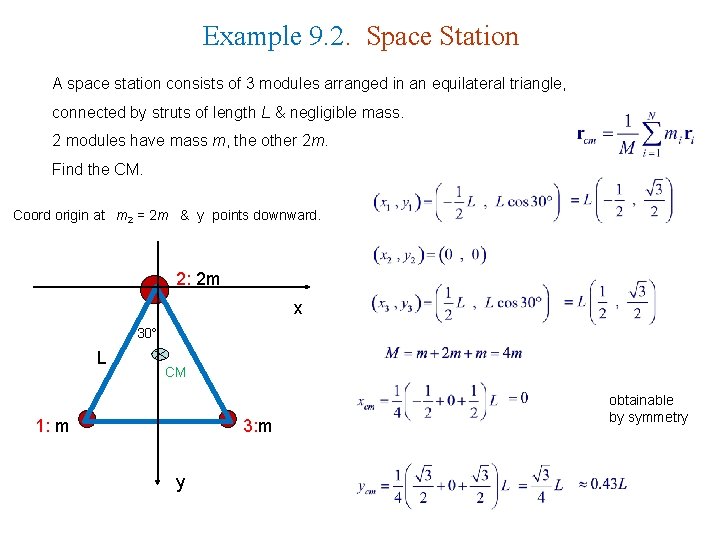
Example 9. 2. Space Station A space station consists of 3 modules arranged in an equilateral triangle, connected by struts of length L & negligible mass. 2 modules have mass m, the other 2 m. Find the CM. Coord origin at m 2 = 2 m & y points downward. 2: 2 m x 30 L CM 1: m 3: m y obtainable by symmetry

Continuous Distributions of Matter Discrete collection: Continuous distribution: Let be the density of the matter.

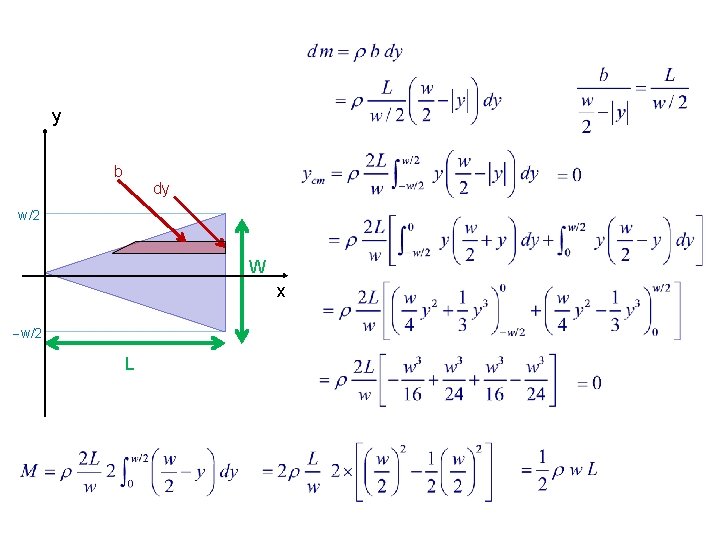
Example 9. 3. Aircraft Wing A supersonic aircraft wing is an isosceles triangle of length L, width w, and negligible thickness. It has mass M, distributed uniformly. Where’s its CM? Density of wing = . Coord origin at leftmost tip of wing. y dx h W L x By symmetry,

y b dy w/2 W x w/2 L

CMfuselage CMplane CMwing A high jumper clears the bar, but his CM doesn’t.

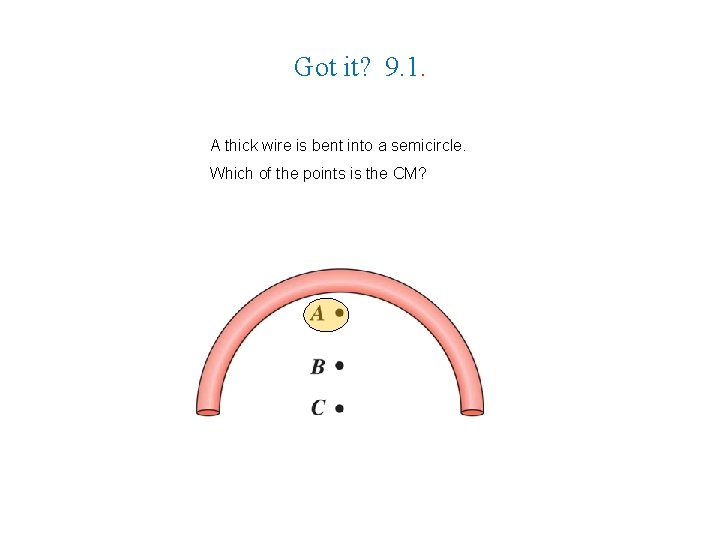
Got it? 9. 1. A thick wire is bent into a semicircle. Which of the points is the CM?

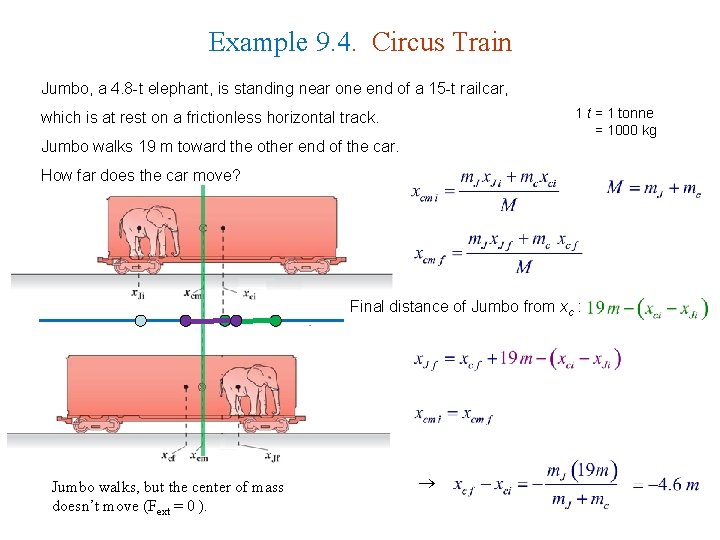
Example 9. 4. Circus Train Jumbo, a 4. 8 -t elephant, is standing near one end of a 15 -t railcar, 1 t = 1 tonne = 1000 kg which is at rest on a frictionless horizontal track. Jumbo walks 19 m toward the other end of the car. How far does the car move? Final distance of Jumbo from xc : Jumbo walks, but the center of mass doesn’t move (Fext = 0 ).

9. 2. Momentum Total momentum: M constant

Conservation of Momentum: Total momentum of a system is a constant if there is no net external force.

GOT IT! 9. 2. A 500 -g fireworks rocket is moving with velocity v = 60 j m/s at the instant it explodes. If you were to add the momentum vectors of all its fragments just after the explosion, what would you get? K. E. is not conserved. Emech = K. E. + P. E. grav is not conserved. Etot = Emech + Uchem is conserved.

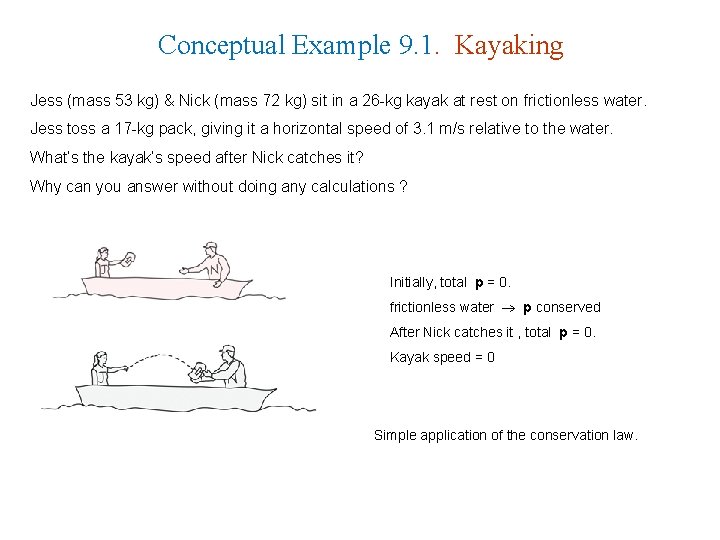
Conceptual Example 9. 1. Kayaking Jess (mass 53 kg) & Nick (mass 72 kg) sit in a 26 -kg kayak at rest on frictionless water. Jess toss a 17 -kg pack, giving it a horizontal speed of 3. 1 m/s relative to the water. What’s the kayak’s speed after Nick catches it? Why can you answer without doing any calculations ? Initially, total p = 0. frictionless water p conserved After Nick catches it , total p = 0. Kayak speed = 0 Simple application of the conservation law.

Making the Connection Jess (mass 53 kg) & Nick (mass 72 kg) sit in a 26 -kg kayak at rest on frictionless water. Jess toss a 17 -kg pack, giving it a horizontal speed of 3. 1 m/s relative to the water. What’s the kayak’s speed while the pack is in the air ? Initially While pack is in air: Note: Emech not conserved

Example 9. 5. Radioactive Decay A lithium-5 ( 5 Li ) nucleus is moving at 1. 6 Mm/s when it decays into a proton ( 1 H, or p ) & an alpha particle ( 4 He, or ). [ Superscripts denote mass in AMU ] is detected moving at 1. 4 Mm/s at 33 to the original velocity of 5 Li. What are the magnitude & direction of p’s velocity? Before decay: After decay:

Example 9. 6. Fighting a Fire A firefighter directs a stream of water to break the window of a burning building. The hose delivers water at a rate of 45 kg/s, hitting the window horizontally at 32 m/s. After hitting the window, the water drops horizontally. What horizontal force does the water exert on the window? Momentum transfer to a plane stream: = Rate of momentum transfer to window = force exerted by water on window

GOT IT? 9. 3. Two skaters toss a basketball back & forth on frictionless ice. Which of the following does not change: (a) momentum of individual skater. (b) momentum of basketball. (c) momentum of the system consisting of one skater & the basketball. (d) momentum of the system consisting of both skaters & the basketball.

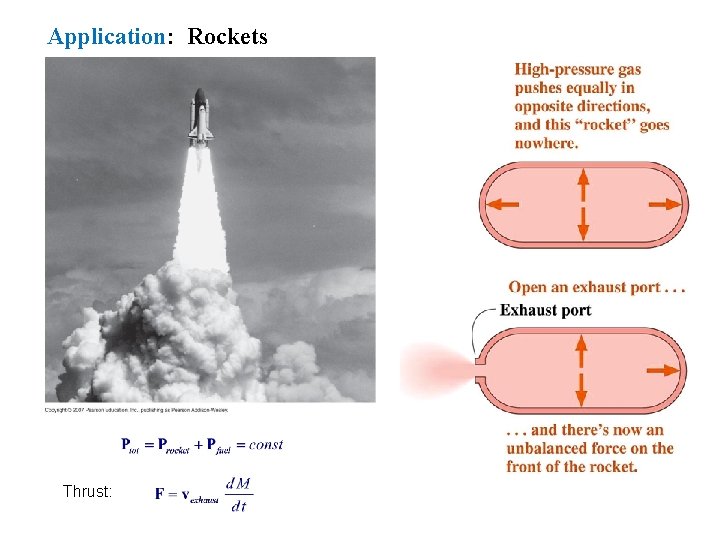
Application: Rockets Thrust:

9. 3. Kinetic Energy of a System

9. 4. Collisions Examples of collision: • Balls on pool table. • tennis rackets against balls. • bat against baseball. • asteroid against planet. Characteristics of collision: • Duration: brief. • Effect: intense • particles in accelerators. • galaxies • spacecraft against planet ( gravity slingshot ) (all other external forces negligible )

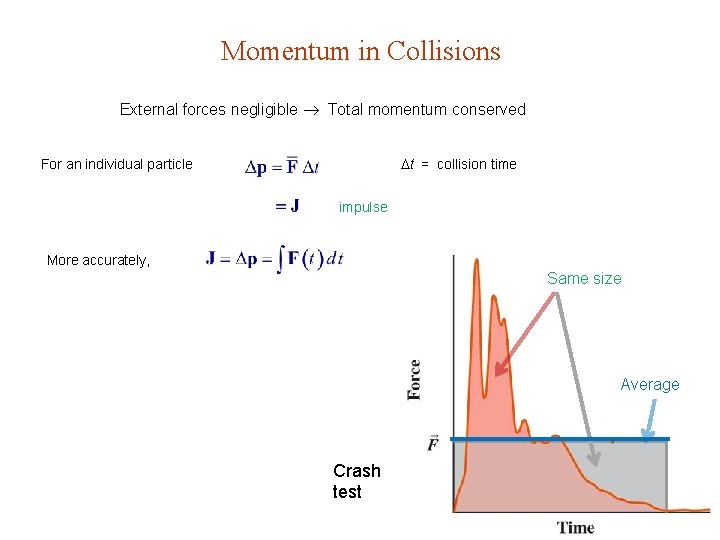
Momentum in Collisions External forces negligible Total momentum conserved t = collision time For an individual particle impulse More accurately, Same size Average Crash test

Energy in Collisions Elastic collision: K conserved. Inelastic collision: K not conserved. Bouncing ball: inelastic collision between ball & ground.

GOT IT? 9. 4. Which of the following qualifies as a collision? Of the collisions, which are nearly elastic & which inelastic? elastic (a) a basketball rebounds off the backboard. elastic (b) two magnets approach, their north poles facing; they repel & reverse direction without touching. (c) a basket ball flies through the air on a parabolic trajectory. inelastic (d) a truck crushed a parked car & the two slide off together. inelastic (e) a snowball splats against a tree, leaving a lump of snow adhering to the bark.

9. 5. Totally Inelastic Collisions Totally inelastic collision: colliding objects stick together maximum energy loss consistent with momentum conservation.

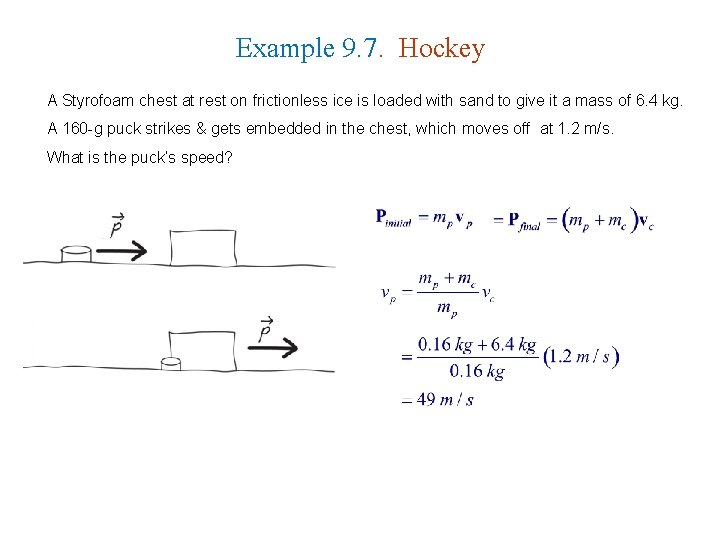
Example 9. 7. Hockey A Styrofoam chest at rest on frictionless ice is loaded with sand to give it a mass of 6. 4 kg. A 160 -g puck strikes & gets embedded in the chest, which moves off at 1. 2 m/s. What is the puck’s speed?

Example 9. 8. Fusion Consider a fusion reaction of 2 deuterium nuclei 2 H + 2 H 4 He. Initially, one of the 2 H is moving at 3. 5 Mm/s, the other at 1. 8 Mm/s at a 64 angle to the 1 st. Find the velocity of the Helium nucleus.

Example 9. 9. Ballistic Pendulum The ballistic pendulum measures the speeds of fast-moving objects. A bullet of mass m strikes a block of mass M and embeds itself in the latter. The block swings upward to a vertical distance of h. Find the bullet’s speed. Caution: (heat is generated when bullet strikes block)

9. 6. Elastic Collisions Momentum conservation: Energy conservation: Implicit assumption: particles have no interaction when they are in the initial or final states. ( Ei = Ki ) 2 -D case: number of unknowns = 2 2 = 4 ( final state: v 1 fx , v 1 fy , v 2 fx , v 2 fy ) number of equations = 2 +1 = 3 1 more conditions needed. 3 -D case: number of unknowns = 3 2 = 6 number of equations = 3 +1 = 4 2 more conditions needed. ( final state: v 1 fx , v 1 fy , v 1 fz , v 2 fx , v 2 fy , v 2 fz )

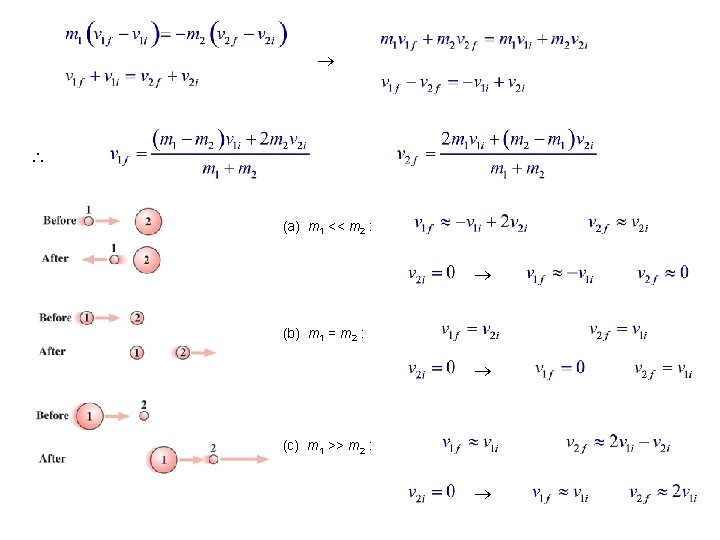
Elastic Collisions in 1 -D collision 1 -D case: number of unknowns = 1 2 = 2 number of equations = 1 +1 = 2 This is a 2 -D collision unique solution. ( v 1 f , v 2 f )

Example 9. 10. Nuclear Engineering Moderator slows neutrons to induce fission. A common moderator is heavy water ( D 2 O ). Find the fraction of a neutron’s kinetic energy that’s transferred to an initially stationary D in a head-on elastic collision.

GOT IT? 9. 5. One ball is at rest on a level floor. Another ball collides elastically with it & they move off in the same direction separately. What can you conclude about the masses of the balls? 1 st one is lighter.

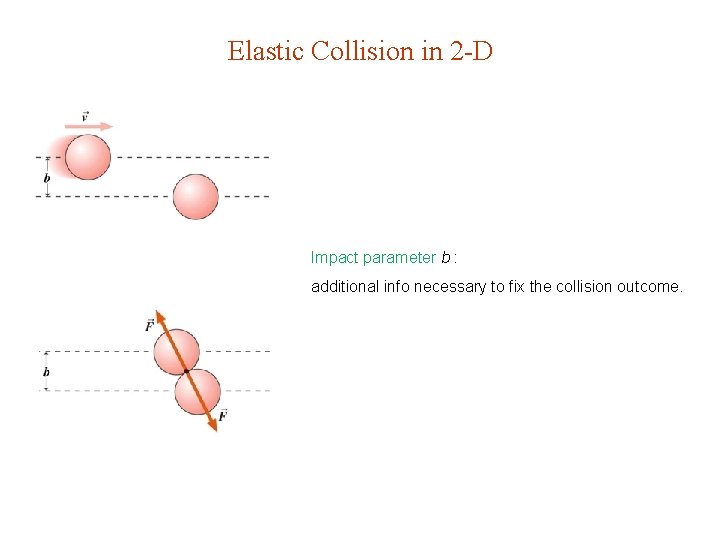
Elastic Collision in 2 -D Impact parameter b : additional info necessary to fix the collision outcome.

Example 9. 11. Croquet A croquet ball strikes a stationary one of equal mass. The collision is elastic & the incident ball goes off 30 to its original direction. In what direction does the other ball move? p cons: E cons:

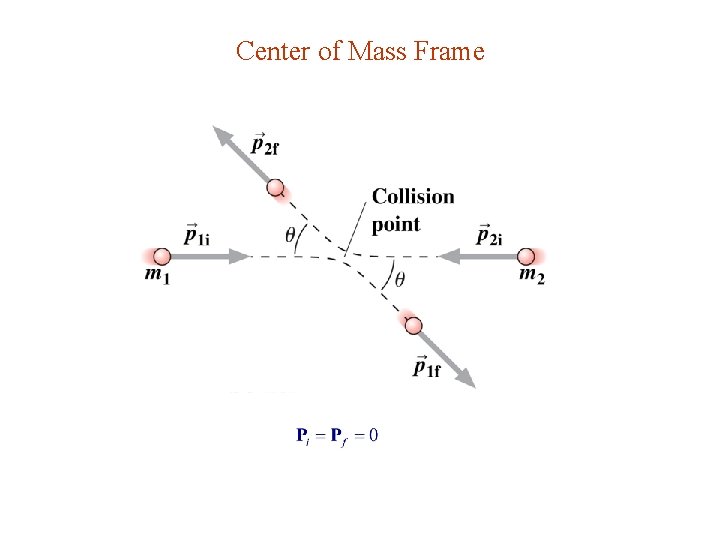
Center of Mass Frame