9 Set ADTs Set concepts Set applications A

9 Set ADTs • Set concepts. • Set applications. • A set ADT: requirements, contract. • Implementations of sets: using arrays, linked lists, boolean arrays. • Sets in the Java class library. © 2001, D. A. Watt and D. F. Brown

Set concepts (1) • A set is a collection of distinct members (values or objects), whose order is insignificant. • Notation for sets: {a, b, …, z}. The empty set is { }. § Set notation is used here, but not supported by Java.

Set concepts (2) • Examples of sets: evens = {0, 2, 4, 6, 8} set of integers punct = {‘. ’, ‘!’, ‘? ’, ‘: ’, ‘; ’, ‘, ’} set of characters EU = {AT, BE, DK, ES, FI, FR, GR, IE, IT, LU, NL, PT, SE, UK} NAFTA = {CA, MX, US} NATO = {BE, CA, CZ, DE, DK, ES, FR, GR, HU, IS, IT, LU, NL, NO, PL, PT, TR, UK, US} sets of countries

Set concepts (3) • The cardinality of a set s is the number of members of s. This is written #s. E. g. : #EU = 15 #{red, white, red} = 2 Duplicate members aren’t counted. • An empty set has cardinality zero. • We can test whether x is a member of set s (i. e. , s contains x). This is the membership test, written x s. E. g. : UK EU SE NATO SE is not a member of NATO.

Set concepts (4) • Two sets are equal if they contain exactly the same members. E. g. : Order of members NAFTA = {US, CA, MX} NAFTA {CA, US} doesn’t matter. These two sets are unequal. • Set s 1 subsumes (is a superset of) set s 2 if every member of s 2 is also a member of s 1. This is written s 1 s 2. E. g. : NATO {CA, US} NATO EU NATO does not subsume EU.

Set concepts (5) • The union of sets s 1 and s 2 is a set containing just those values that are members of s 1 or s 2 or both. This is written s 1 s 2. E. g. : {DK, NO, SE} {FI, IS} = {DK, FI, IS, NO, SE} {DK, NO, SE} {IS, NO} = {DK, IS, NO, SE}

Set concepts (6) • The intersection of sets s 1 and s 2 is a set containing just those values that are members of both s 1 and s 2. This is written s 1 s 2. E. g. : NAFTA NATO = {CA, US} NAFTA EU = {} • Two sets are disjoint if they have no common member, I. e. , if their intersection is empty. E. g. : NAFTA and EU are disjoint NATO and EU are not disjoint.

Set concepts (7) • The difference of sets s 1 and s 2 is a set containing just those values that are members of s 1 but not of s 2. This is written s 1 – s 2. E. g. : NATO – EU EU – NATO = {CA, CZ, HU, IS, NO, PL, TR, US} = {AT, FI, IE, SE}

Set applications • Spelling checker: § A spelling checker’s dictionary is a set of words. § The spelling checker highlights any words in the document that are not in the dictionary. § The spelling checker might allow the user to add words to the dictionary. • Relational database system: § A relation is essentially a set of tuples. § Each tuple is distinct. § The tuples are in no particular order.

Example 1: prime numbers • A prime number is an integer that is divisible only by itself and 1. E. g. : 2, 7, 11, 13 are prime numbers. • Eratosthenes’ sieve algorithm: To compute the set of prime numbers less than m (where m > 0): 1. 1. Set sieve = { }. 1. Set sieve = {2, 3, …, m– 1}. 1. 2. For i = 2, . . . , m– 1, repeat: 2. For i = 2, 3, …, while i 2 < m, repeat: 1. 2. 1. Add i to sieve. 2. 1. If i is a member of sieve: 2. 1. 1. Remove all multiples of i from sieve. 3. Terminate with answer sieve. 2. 1. 1. For mult = 2 i, 3 i, . . . , while mult < m, repeat: 2. 1. 1. 1. Remove mult from sieve.

Set ADT: requirements • Requirements: 1) It must be possible to make a set empty. 2) It must be possible to test whether a set is empty. 3) It must be possible to obtain the cardinality of a set. 4) It must be possible to perform a membership test. 5) It must be possible to add or remove a member of a set. 6) It must be possible to test whether two sets are equal. 7) It must be possible to test whether one set subsumes another. 8) It must be possible to compute the union, intersection, or difference of two sets. 9) It must be possible to traverse a set.

Set ADT: contract (1) • Possible contract: public interface Set { // Each Set object is a set whose members are objects. ////// Accessors ////// public boolean is. Empty (); // Return true if and only if this set is empty. public int size (); // Return the cardinality of this set. public boolean contains (Object obj); // Return true if and only if obj is a member of this set.

Set ADT: contract (2) • Possible contract (continued): public boolean equals (Set that); // Return true if and only if this set is equal to that. public boolean contains. All (Set that); // Return true if and only if this set subsumes that.

Set ADT: contract (3) • Possible contract (continued): ////// Transformers ////// public void clear (); // Make this set empty. public void add (Object obj); // Add obj as a member of this set. public void remove (Object obj); // Remove obj from this set. public void add. All (Set that); // Make this set the union of itself and that.

Set ADT: contract (4) • Possible contract (continued): public void remove. All (Set that); // Make this set the difference of itself and that. public void retain. All (Set that); // Make this set the intersection of itself and that. ////// Iterator ////// public Iterator iterator(); // Return an iterator that will visit all members of this set, in no // particular order. }

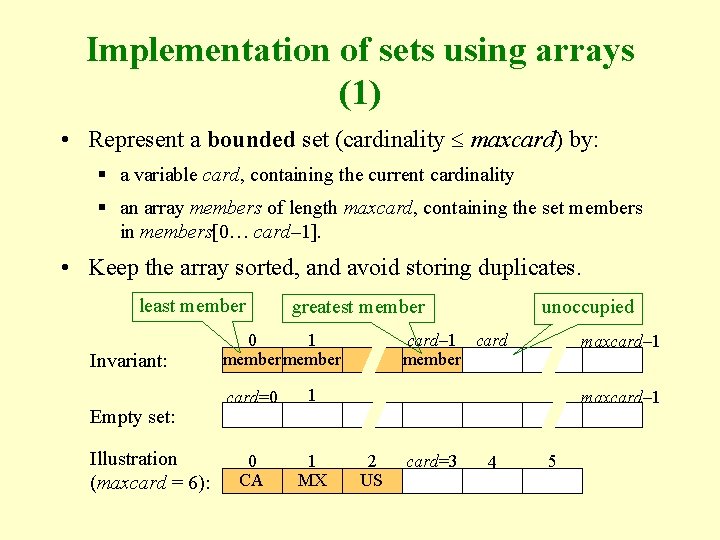
Implementation of sets using arrays (1) • Represent a bounded set (cardinality maxcard) by: § a variable card, containing the current cardinality § an array members of length maxcard, containing the set members in members[0… card– 1]. • Keep the array sorted, and avoid storing duplicates. least member Invariant: Empty set: Illustration (maxcard = 6): unoccupied greatest member 0 1 member card=0 1 0 CA 1 MX card– 1 card member maxcard– 1 2 US card=3 4 5

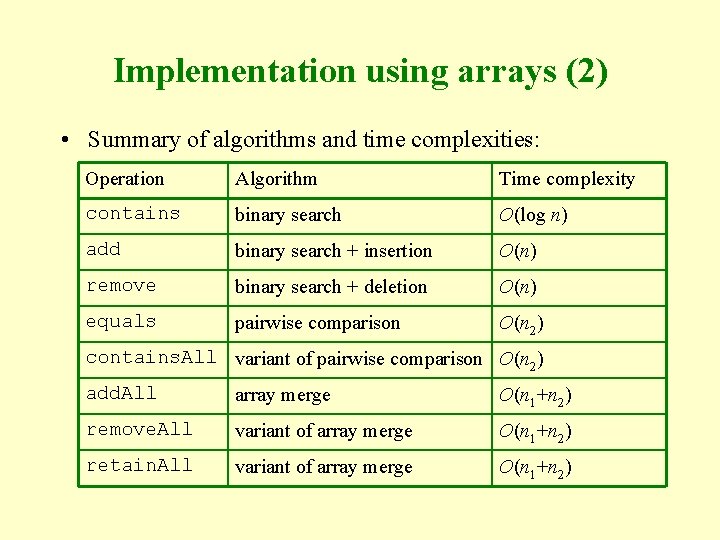
Implementation using arrays (2) • Summary of algorithms and time complexities: Operation Algorithm Time complexity contains binary search O(log n) add binary search + insertion O(n) remove binary search + deletion O(n) equals pairwise comparison O(n 2) contains. All variant of pairwise comparison O(n 2) add. All array merge O(n 1+n 2) remove. All variant of array merge O(n 1+n 2) retain. All variant of array merge O(n 1+n 2)

Implementation of sets using SLLs (1) • Represent an (unbounded) set by: § a variable card, containing the current cardinality § an SLL, containing one member per node. • Keep the SLL sorted, and avoid storing duplicates. least member Invariant: member greatest member Empty set: Illustration: CA MX US represents the set {CA, US, MX}

Implementation using SLLs (2) • Summary of algorithms and time complexities: Operation Algorithm Time complexity contains SLL linear search O(n) add SLL linear search + insertion O(n) remove SLL linear search + deletion O(n) equals pairwise comparison O(n 2) contains. All variant of pairwise comparison O(n 2) add. All SLL merge O(n 1+n 2) remove. All variant of SLL merge O(n 1+n 2) retain. All variant of SLL merge O(n 1+n 2)

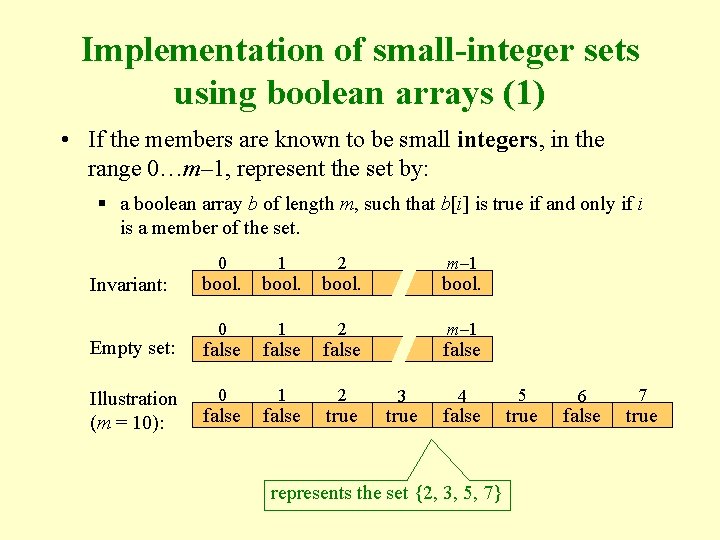
Implementation of small-integer sets using boolean arrays (1) • If the members are known to be small integers, in the range 0…m– 1, represent the set by: § a boolean array b of length m, such that b[i] is true if and only if i is a member of the set. Invariant: 0 1 2 m– 1 bool. Empty set: false Illustration (m = 10): 0 1 2 false true bool. m– 1 false 3 true 4 false represents the set {2, 3, 5, 7} 5 true 6 false 7 true

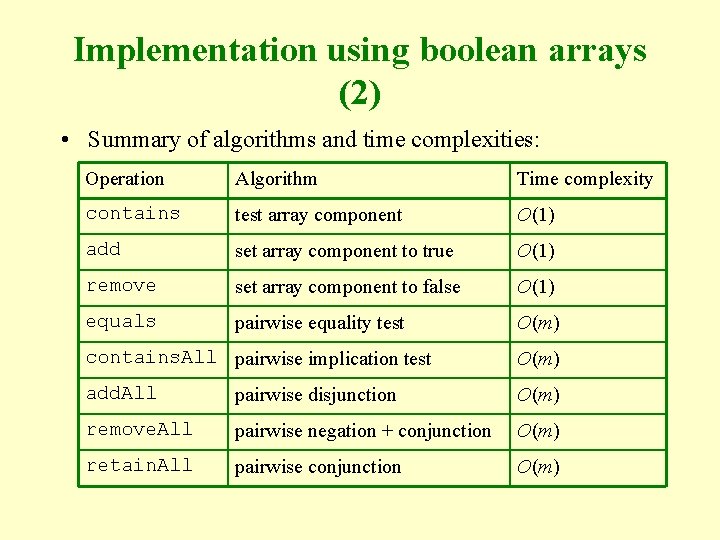
Implementation using boolean arrays (2) • Summary of algorithms and time complexities: Operation Algorithm Time complexity contains test array component O(1) add set array component to true O(1) remove set array component to false O(1) equals pairwise equality test O(m) contains. All pairwise implication test O(m) add. All pairwise disjunction O(m) remove. All pairwise negation + conjunction O(m) retain. All pairwise conjunction O(m)

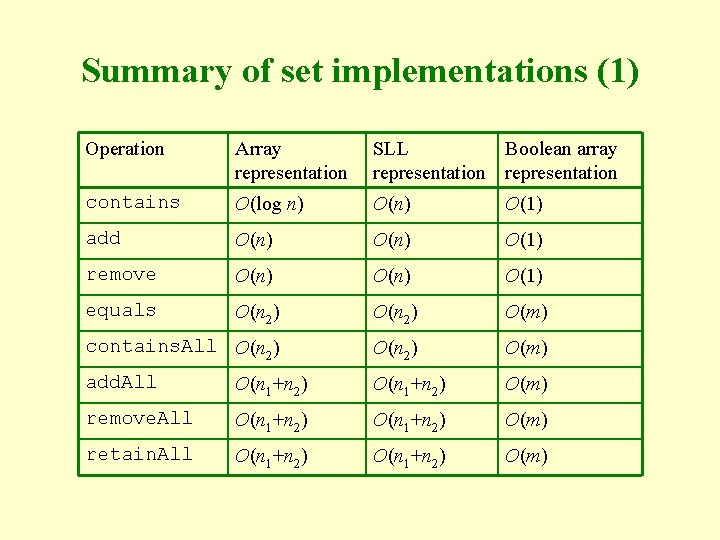
Summary of set implementations (1) Operation Array representation SLL Boolean array representation contains O(log n) O(1) add O(n) O(1) remove O(n) O(1) equals O(n 2) O(m) contains. All O(n 2) O(m) add. All O(n 1+n 2) O(m) remove. All O(n 1+n 2) O(m) retain. All O(n 1+n 2) O(m)

Summary of set implementations (2) • The array representation is suitable only for small or static sets. § A static set is one in which members are never/infrequently added or removed. • The SLL representation is suitable only for small sets. • The boolean-array representation is suitable only for dense sets of small integers. § A dense set is one where most potential members are actually present. • For general applications, we need a more efficient set representation: search tree (see 10) or hash table (see 12).

Sets in the Java class library • The java. util. Set interface is similar to the Set interface above. • The java. util. Tree. Set class implements the java. util. Set interface, representing each set by a search tree (see 10). • The java. util. Hash. Set class implements the java. util. Set interface, representing each set by an open-bucket hash table (see 12).

Example 2: information retrieval (1) • Consider a very simple information retrieval system. • A query is a set of key words. • Each document in the document base is viewed as a set of words. The order of words in a document is of no significance. • In response to a query, the system identifies each document that contains all or some of the key words.

Example 2 (2) • Outline of implementation: public static final int NONE=0, SOME=1, ALL=2; public static int score (String name, Set keywords) { // Return a score reflecting whether the document named name // contains all, some, or none of the words in keywords. Set docwords = read. All. Words(name); if (docwords. contains. All(keywords)) return ALL; else if (disjoint(doc. Words, keywords)) return NONE; else return SOME ; }

Example 2 (3) • Outline of implementation (continued): private static boolean disjoint ( Set docwords, Set keywords) { // Return true if and only if the sets docwords and keywords // have no common words. Iterator iter = keywords. iterator(); while (iter. has. Next()) { String keyword = (String) iter. next(); if (docwords. contains(word)) return false; } return true; }

Example 2 (4) • Outline of implementation (continued): private static Set read. All. Words (String name) { // Return the set of all words occurring in the document name. Buffered. Reader doc = new Buffered. Reader( new Input. Stream. Reader( new File. Input. Stream(name))); or: Set words = new Tree. Set(); new Hash. Set() for (; ; ) { String word = read. Word(doc); if (word == null) break; // end of document words. add(word. to. Lower. Case()); } doc. close(); return words;

Example 2 (5) • Outline of implementation (continued): private static String read. Word ( Buffered. Reader doc) throws IOException { // Read and return the next word from doc, skipping any preceding // white space or punctuation. Return null if no word remains to be // read. … }