9 DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS 9 5 Linear










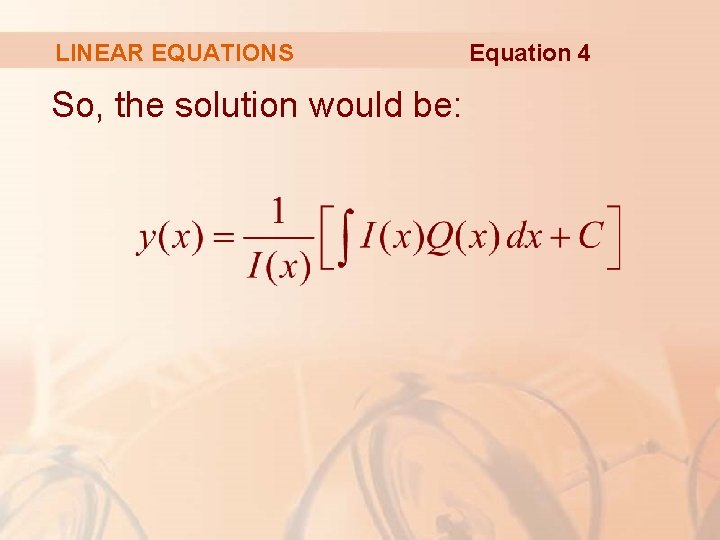
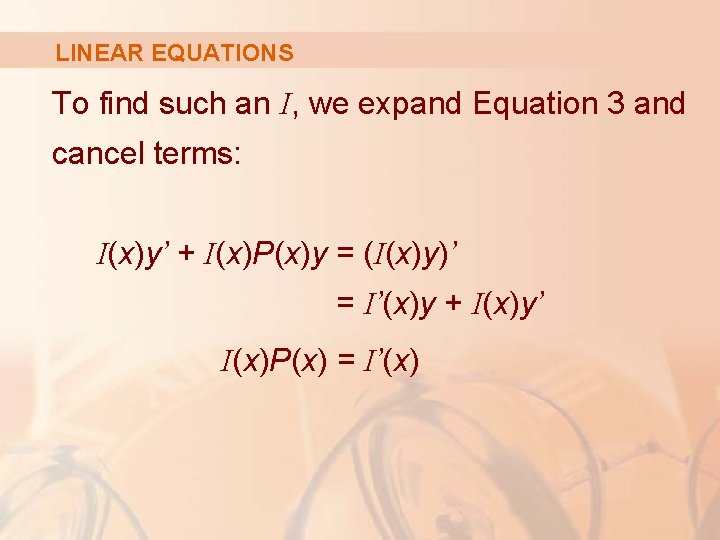










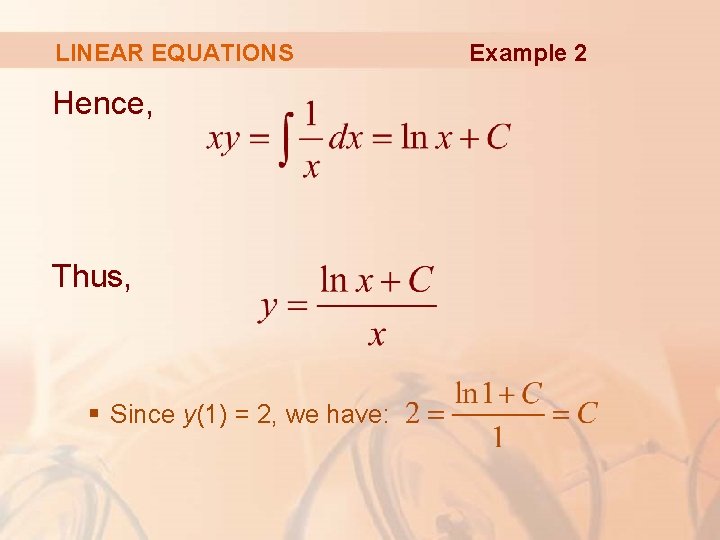



















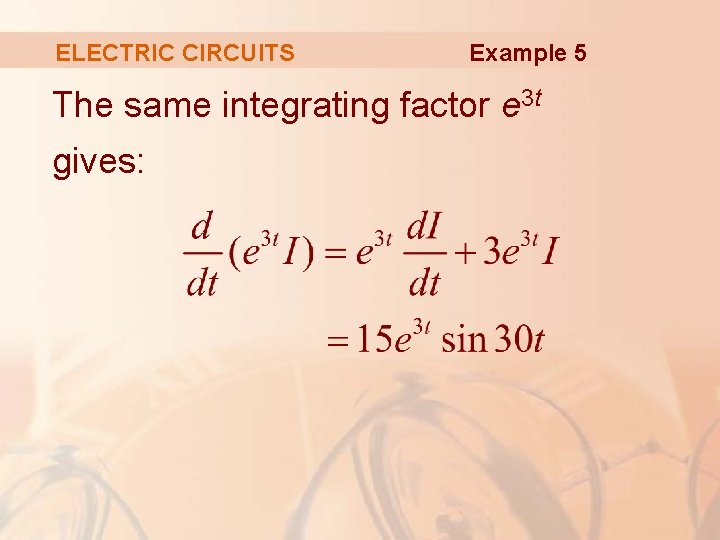


- Slides: 52

9 DIFFERENTIAL EQUATIONS

DIFFERENTIAL EQUATIONS 9. 5 Linear Equations In this section, we will learn: How to solve linear equations using an integrating factor.

LINEAR EQUATIONS Equation 1 A first-order linear differential equation is one that can be put into the form where P and Q are continuous functions on a given interval. § This type of equation occurs frequently in various sciences, as we will see.

Equation 2 LINEAR EQUATIONS An example of a linear equation is xy’ + y = 2 x because, for x ≠ 0, it can be written in the form

LINEAR EQUATIONS Notice that this differential equation is not separable. § It’s impossible to factor the expression for y’ as a function of x times a function of y.

LINEAR EQUATIONS However, we can still solve the equation by noticing, by the Product Rule, that xy’ + y = (xy)’ So, we can rewrite the equation as: (xy)’ = 2 x

LINEAR EQUATIONS If we now integrate both sides, we get: xy = x 2 + C or y = x + C/x § If the differential equation had been in the form of Equation 2, we would have had to initially multiply each side of the equation by x.

INTEGRATING FACTOR It turns out that every first-order linear differential equation can be solved in a similar fashion by multiplying both sides of Equation 1 by a suitable function I(x). § This is called an integrating factor.

LINEAR EQUATIONS Equation 3 We try to find I so that the left side of Equation 1, when multiplied by I(x), becomes the derivative of the product I(x)y: I(x)(y’ + P(x)y) = (I(x)y)’

LINEAR EQUATIONS If we can find such a function I, then Equation 1 becomes: (I(x)y)’ = I(x)Q(x) Integrating both sides, we would have: I(x)y = ∫ I(x)Q(x) dx + C
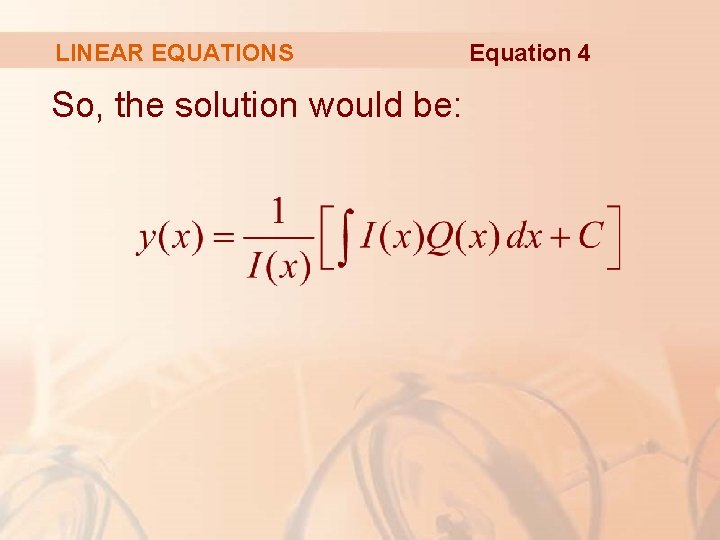
LINEAR EQUATIONS So, the solution would be: Equation 4
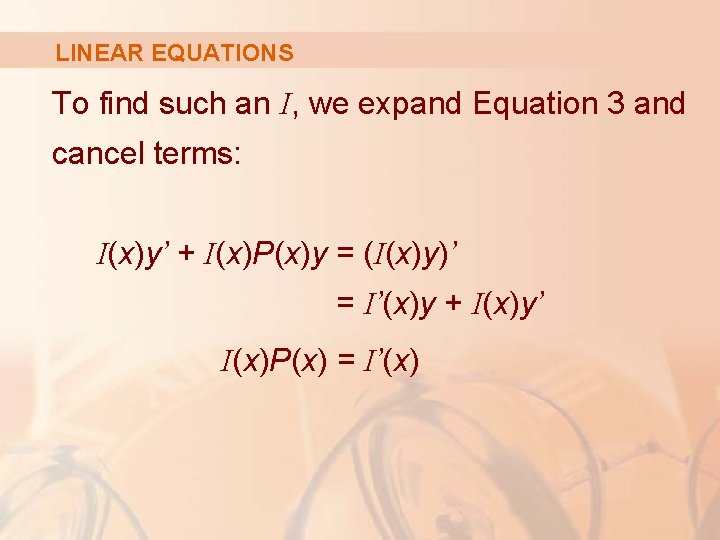
LINEAR EQUATIONS To find such an I, we expand Equation 3 and cancel terms: I(x)y’ + I(x)P(x)y = (I(x)y)’ = I’(x)y + I(x)y’ I(x)P(x) = I’(x)

SEPERABLE DIFFERENTIAL EQUATIONS This is a separable differential equation for I, which we solve as follows: where A = ±e. C.

LINEAR EQUATIONS Equation 5 We are looking for a particular integrating factor—not the most general one. So, we take A = 1 and use:

LINEAR EQUATIONS Thus, a formula for the general solution to Equation 1 is provided by Equation 4, where I is given by Equation 5. § However, instead of memorizing the formula, we just remember the form of the integrating factor—as follows.

LINEAR EQUATIONS To solve the linear differential equation y’ + P(x)y = Q(x) multiply both sides by the integrating factor and integrate both sides.

LINEAR EQUATIONS Example 1 Solve the differential equation § The given equation is linear as it has the form of Equation 1: P(x) = 3 x 2 and Q(x) = 6 x 2 § An integrating factor is:

LINEAR EQUATIONS Example 1 § Multiplying both sides of the equation by we get or 3 x e ,

LINEAR EQUATIONS Example 1 § Integrating both sides, we have:

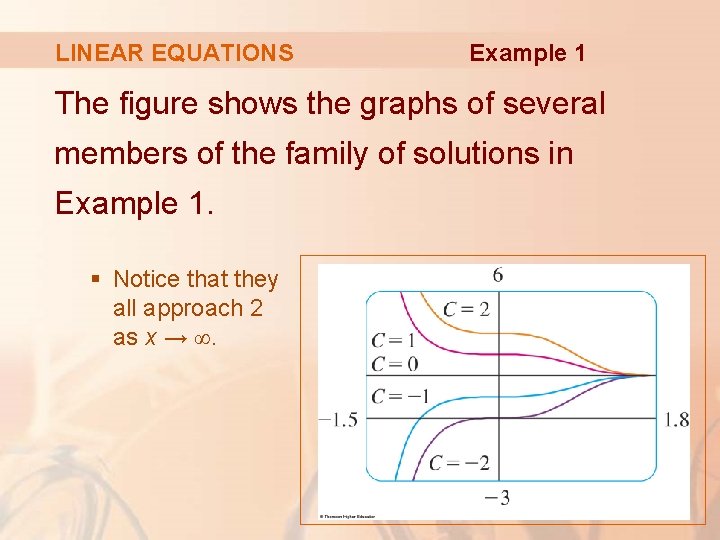
LINEAR EQUATIONS Example 1 The figure shows the graphs of several members of the family of solutions in Example 1. § Notice that they all approach 2 as x → ∞.

Example 2 LINEAR EQUATIONS Find the solution of the initial-value problem x 2 y’ + xy = 1 x>0 y(1) = 2

LINEAR EQUATIONS E. g. 2—Equation 6 First, we must divide both sides by the coefficient of y’ to put the differential equation into standard form:

LINEAR EQUATIONS Example 2 The integrating factor is: I(x) = e ∫ (1/x) dx = eln x = x Multiplication of Equation 6 by x gives:
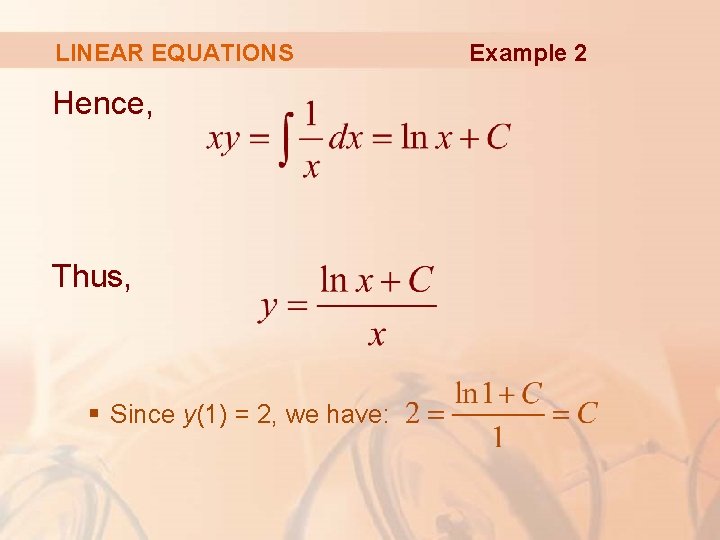
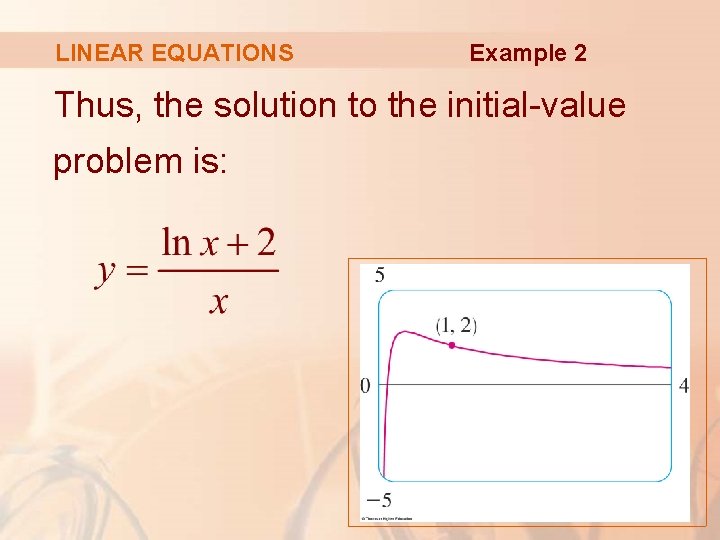
LINEAR EQUATIONS Hence, Thus, § Since y(1) = 2, we have: Example 2

LINEAR EQUATIONS Example 2 Thus, the solution to the initial-value problem is:

Example 3 LINEAR EQUATIONS Solve y’ +2 xy = 1 § The equation is in the standard form for a linear equation. § Multiplying by the integrating factor e we get 2 2 2 x x x e y’ + 2 xe y = e or 2 x (e y)’ = 2 x e ∫ 2 x dx = 2 x e ,

Example 3 LINEAR EQUATIONS x 2 Therefore, e y = ∫ 2 x e dx +C 2 § Recall from Section 7. 5 that ∫ ex dx can’t be expressed in terms of elementary functions. § Nonetheless, it’s a perfectly good function and we can leave the answer as: y= 2 -x e ∫ 2 x e dx + 2 -x Ce

LINEAR EQUATIONS Example 3 Another way of writing the solution is: § Any number can be chosen for the lower limit of integration.

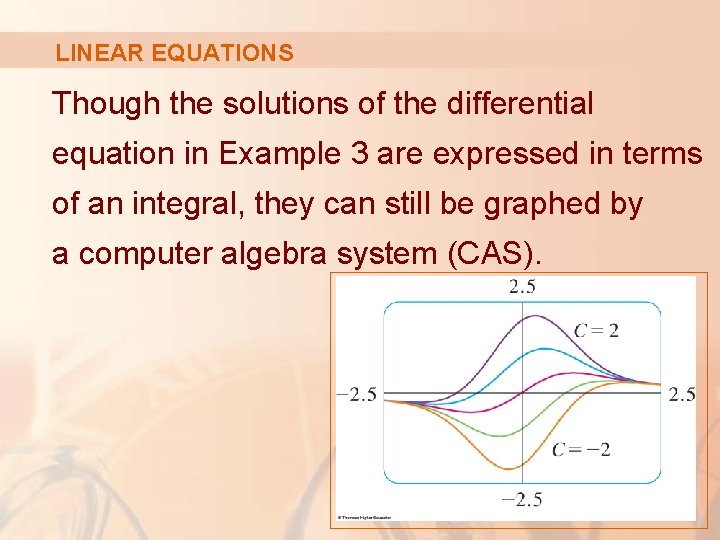
LINEAR EQUATIONS Though the solutions of the differential equation in Example 3 are expressed in terms of an integral, they can still be graphed by a computer algebra system (CAS).

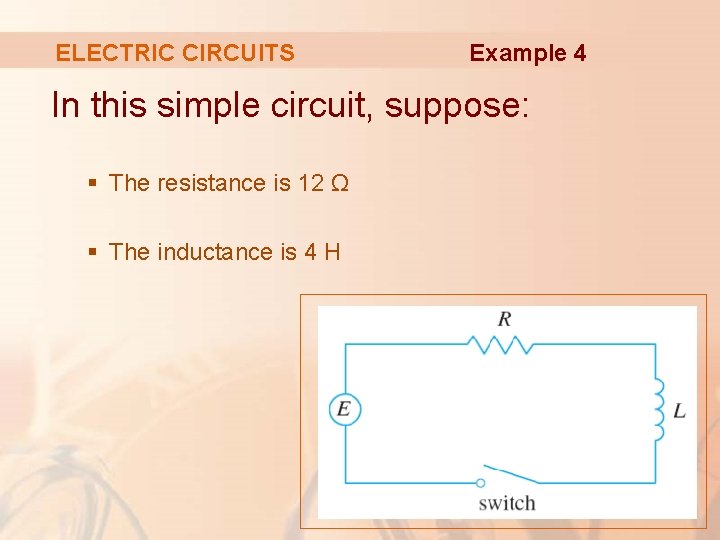
APPLICATION TO ELECTRIC CIRCUITS In Section 9. 2, we considered the simple electric circuit shown here.

APPLICATION TO ELECTRIC CIRCUITS An electromotive force (usually a battery or generator) produces: § A voltage of E(t) volts (V) § A current of I(t) amperes (A) at time t

APPLICATION TO ELECTRIC CIRCUITS The circuit also contains: § A resistor with a resistance of R ohms (Ω) § An inductor with an inductance of L henries (H)

ELECTRIC CIRCUITS Ohm’s Law gives the drop in voltage due to the resistor as RI. The drop due to the inductor is L(d. I/dt).

ELECTRIC CIRCUITS One of Kirchhoff’s laws says that the sum of the voltage drops is equal to the supplied voltage E(t).

ELECTRIC CIRCUITS Equation 7 Thus, we have which is a first-order linear differential equation. § The solution gives the current I at time t.

ELECTRIC CIRCUITS Example 4 In this simple circuit, suppose: § The resistance is 12 Ω § The inductance is 4 H

ELECTRIC CIRCUITS Example 4 Then, a battery gives a constant voltage of 60 V and the switch is closed when t = 0, so the current starts with I(0) = 0.

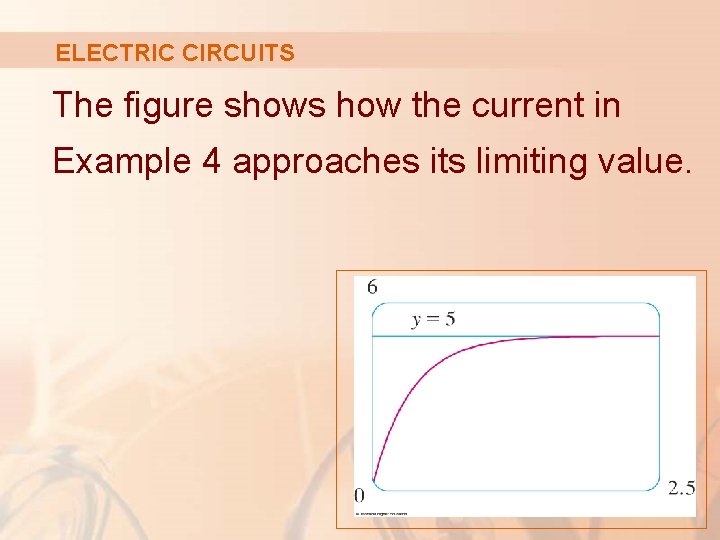
ELECTRIC CIRCUITS Now, find: a. I(t) b. The current after 1 s c. The limiting value of the current Example 4

ELECTRIC CIRCUITS Example 4 a If we put L = 4, R = 12, and E(t) = 60 in Equation 7, we obtain the initial-value problem or

ELECTRIC CIRCUITS Example 4 a Multiplying by the integrating factor e ∫ 3 dt = e 3 t, we get:

Example 4 a ELECTRIC CIRCUITS Since I(0) = 0, we have: 5+C=0 Thus, C = – 5 and I(t) = 5(1 – e-3 t)

ELECTRIC CIRCUITS Example 4 b After 1 second, the current is: I(1) = 5(1 – e-3) ≈ 4. 75 A

ELECTRIC CIRCUITS Example 4 c The limiting value of the current is given by:

ELECTRIC CIRCUITS The figure shows how the current in Example 4 approaches its limiting value.

ELECTRIC CIRCUITS The differential equation in Example 4 is both linear and separable. § So, an alternative method is to solve it as a separable equation (Example 4 in Section 9. 3).

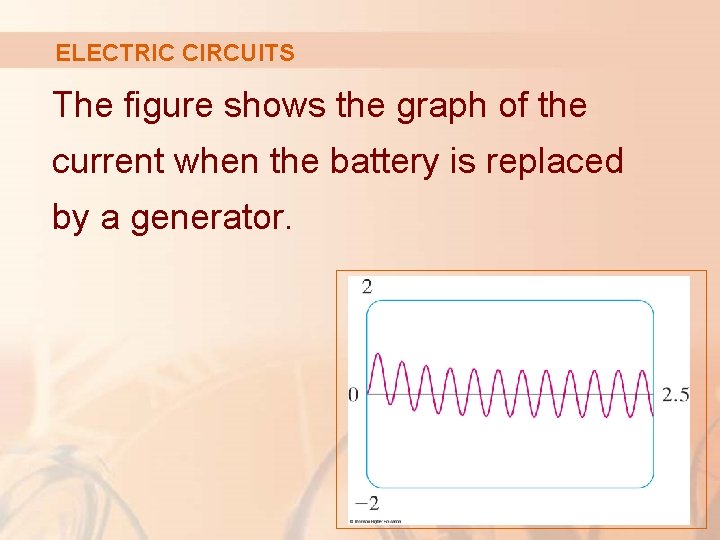
ELECTRIC CIRCUITS However, if we replace the battery by a generator, we get an equation that is linear but not separable—as in the next example.

ELECTRIC CIRCUITS Example 5 Suppose the resistance and inductance remain as in Example 4 but—instead of the battery—we use a generator that produces a variable voltage of: E(t) = 60 sin 30 t volts Find I(t).

ELECTRIC CIRCUITS Example 5 This time, the differential equation becomes or
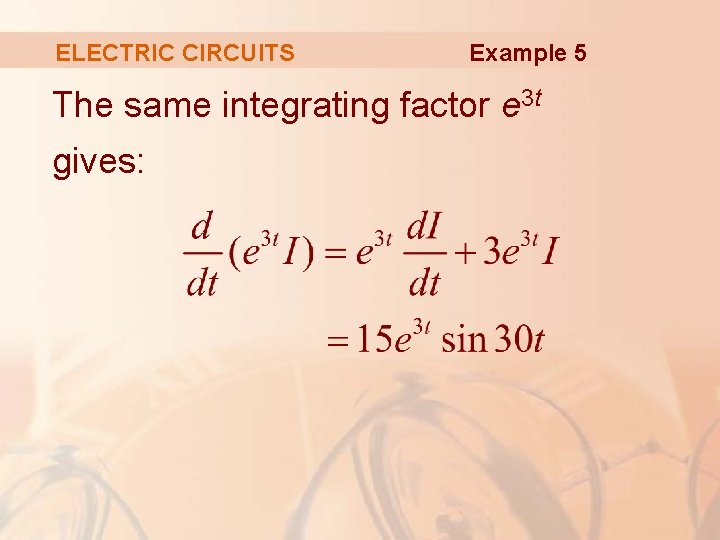
ELECTRIC CIRCUITS Example 5 The same integrating factor e 3 t gives:

ELECTRIC CIRCUITS Example 5 Using Formula 98 in the Table of Integrals, we have:

ELECTRIC CIRCUITS Since I(0) = 0, we get: Thus, Example 5

ELECTRIC CIRCUITS The figure shows the graph of the current when the battery is replaced by a generator.