9 7 Divergence and Curl Vector Fields Fx

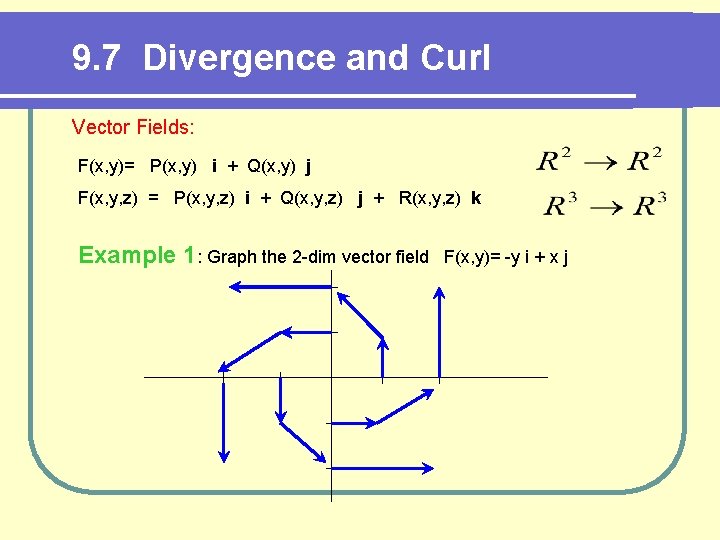
9. 7 Divergence and Curl Vector Fields: F(x, y)= P(x, y) i + Q(x, y) j F(x, y, z) = P(x, y, z) i + Q(x, y, z) j + R(x, y, z) k Example 1: Graph the 2 -dim vector field F(x, y)= -y i + x j

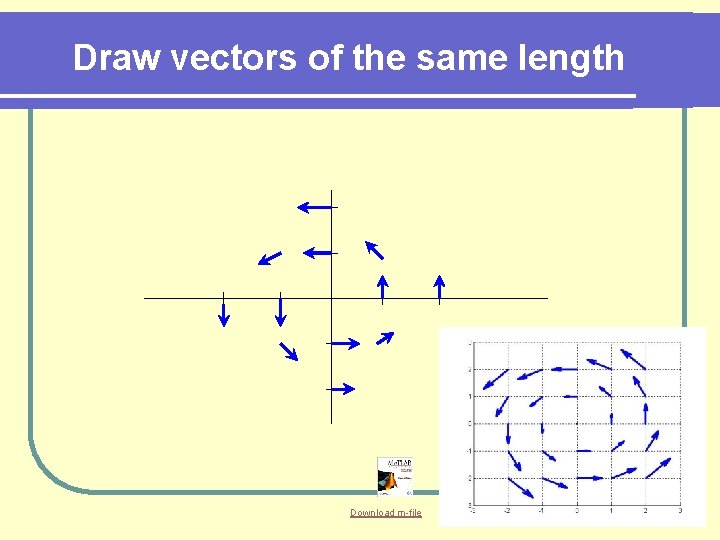
Draw vectors of the same length Download m-file

Divergence Scalar Example 2 IF Find div F

Curl vector Example 2 IF Find curl F

Curl Cross product of the del operator and the vector F Remarks: 1) 2)

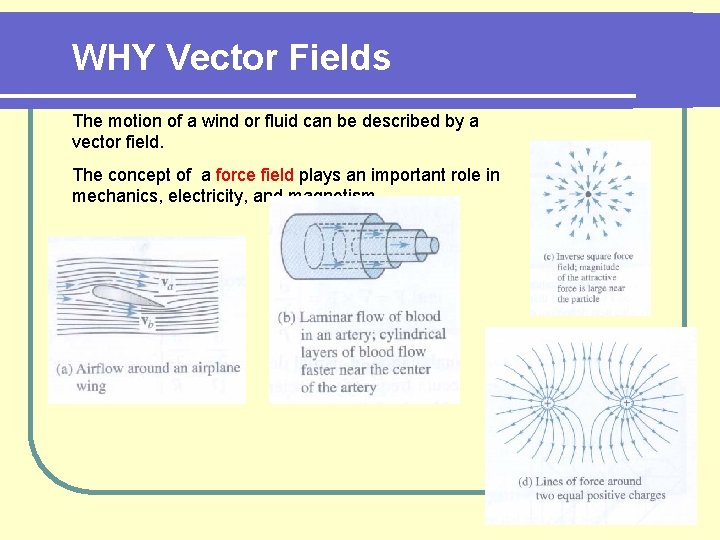
WHY Vector Fields The motion of a wind or fluid can be described by a vector field. The concept of a force field plays an important role in mechanics, electricity, and magnetism.

Physical Interpretations Curl was introduced by Maxwell James Clerk Maxwell (1831 -1879) Scottish Physicist [b. Edinburgh, Scotland, June 13, 1831, d. Cambridge, England, November 5, 1879] He published his first scientific paper at age 14, entered the University of Edinburgh at 16, and graduated from Cambridge University.

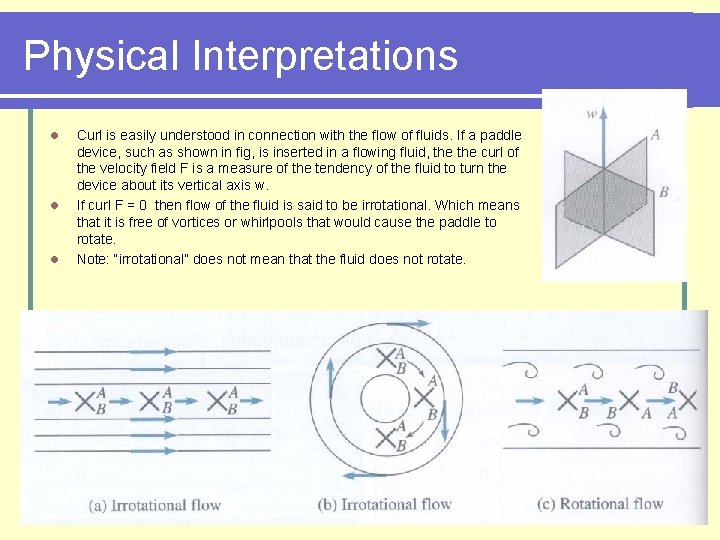
Physical Interpretations l l l Curl is easily understood in connection with the flow of fluids. If a paddle device, such as shown in fig, is inserted in a flowing fluid, the curl of the velocity field F is a measure of the tendency of the fluid to turn the device about its vertical axis w. If curl F = 0 then flow of the fluid is said to be irrotational. Which means that it is free of vortices or whirlpools that would cause the paddle to rotate. Note: “irrotational” does not mean that the fluid does not rotate.

Physical Interpretations l l l l The volume of the fluid flowing through an element of surface area per unit time that is , the flux of the vector field F through the area. The divergence of a velocity field F near a point p(x, y, z) is the flux per unit volume. If div F(p) > 0 then p is said to be a source for F. since there is a net outward flow of fluid near p If div F(p) < 0 then p is said to be a sink for F. since there is a net inward flow of fluid near p If div F(p) = 0 then there are no sources or sinks near p. The divergence of a vector field can also be interpreted as a measure of the rate of change of the density of the fluid at a point. If div F = 0 the fluid is said to be incompressible