9 6 Geometric Probability Objectives Calculate geometric probabilities

9 -6 Geometric Probability Objectives Calculate geometric probabilities. Use geometric probability to predict results in real-world situations. Holt Geometry

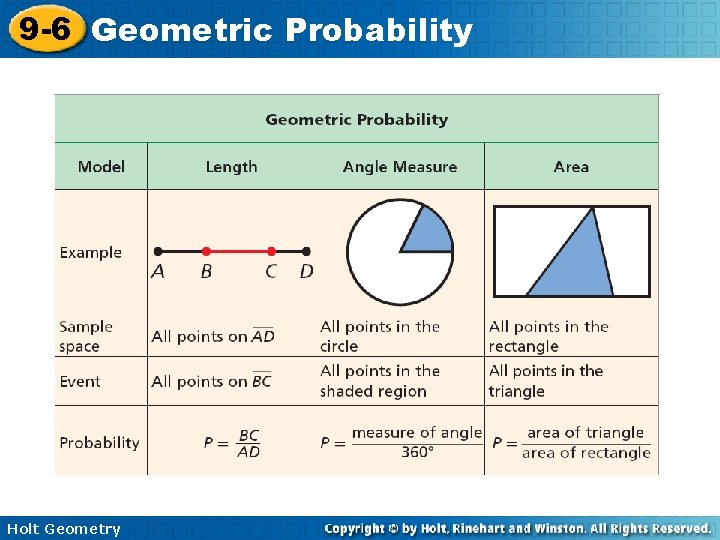
9 -6 Geometric Probability Remember that in probability, the set of all possible outcomes of an experiment is called the sample space. Any set of outcomes is called an event. If every outcome in the sample space is equally likely, theoretical probability of an event is Holt Geometry
9 -6 Geometric Probability Holt Geometry

9 -6 Geometric Probability Remember! If an event has a probability p of occurring, the probability of the event not occurring is 1 – p. Holt Geometry

9 -6 Geometric Probability Example 1 A: Using Length to Find Geometric Probability A point is chosen randomly on PS. Find the probability of each event. The point is on RS. Holt Geometry

9 -6 Geometric Probability Example 1 B: Using Length to Find Geometric Probability The point is not on QR. Subtract from 1 to find the probability that the point is not on QR. Holt Geometry

9 -6 Geometric Probability Example 1 C: Using Length to Find Geometric Probability The point is on PQ or QR. P(PQ or QR) = P(PQ) + P(QR) Holt Geometry

9 -6 Geometric Probability Check It Out! Example 1 Use the figure below to find the probability that the point is on BD. Holt Geometry

9 -6 Geometric Probability Example 2 A: Transportation Application A pedestrian signal at a crosswalk has the following cycle: “WALK” for 45 seconds and “DON’T WALK” for 70 seconds. What is the probability the signal will show “WALK” when you arrive? To find the probability, draw a segment to represent the number of seconds that each signal is on. The signal is “WALK” for 45 out of every 115 seconds. Holt Geometry

9 -6 Geometric Probability Example 3 A: Using Angle Measures to Find Geometric Probability Use the spinner to find the probability of each event. the pointer landing on yellow The angle measure in the yellow region is 140°. Holt Geometry

9 -6 Geometric Probability Example 3 B: Using Angle Measures to Find Geometric Probability Use the spinner to find the probability of each event. the pointer landing on blue or red The angle measure in the blue region is 52°. The angle measure in the red region is 60°. Holt Geometry

9 -6 Geometric Probability Example 3 C: Using Angle Measures to Find Geometric Probability Use the spinner to find the probability of each event. the pointer not landing on green The angle measure in the green region is 108°. Subtract this angle measure from 360°. Holt Geometry
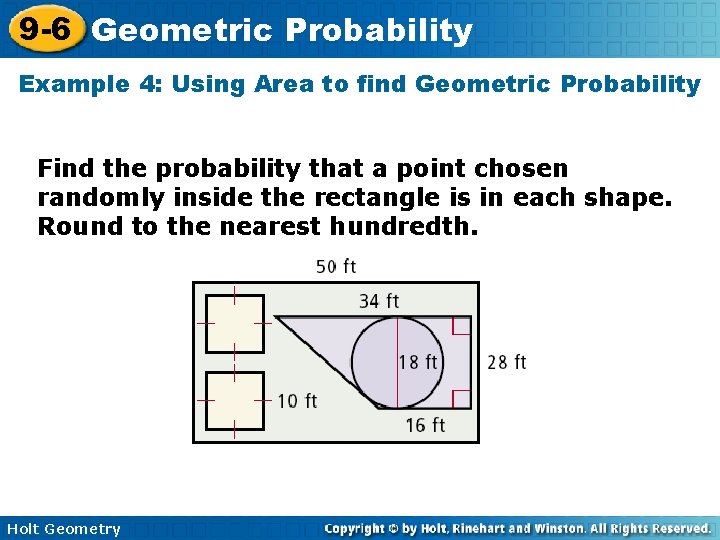
9 -6 Geometric Probability Example 4: Using Area to find Geometric Probability Find the probability that a point chosen randomly inside the rectangle is in each shape. Round to the nearest hundredth. Holt Geometry

9 -6 Geometric Probability Example 4 A: Using Area to find Geometric Probability the circle The area of the circle is A = r 2 = (9)2 = 81 ≈ 254. 5 ft 2. The area of the rectangle is A = bh = 50(28) = 1400 ft 2. The probability is P = 254. 5 ≈ 0. 18. 1400 Holt Geometry

9 -6 Geometric Probability Example 4 B: Using Area to find Geometric Probability the trapezoid The area of the trapezoid is The area of the rectangle is A = bh = 50(28) = 1400 ft 2. The probability is Holt Geometry

9 -6 Geometric Probability Example 4 C: Using Area to find Geometric Probability one of the two squares The area of the two squares is A = 2 s 2 = 2(10)2 = 200 ft 2. The area of the rectangle is A = bh = 50(28) = 1400 ft 2. The probability is Holt Geometry
- Slides: 16