9 5 Trigonometric Ratios Geometry Mrs Spitz Spring

9. 5 Trigonometric Ratios Geometry Mrs. Spitz Spring 2005

Objectives/Assignment • Find the since, the cosine, and the tangent of an acute triangle. • Use trionometric ratios to solve real-life problems, such as estimating the height of a tree or flagpole. • To solve real-life problems such as in finding the height of a water slide. • Assignment: pp. 562 -563 #3 -38 all • Due TODAY– 9. 4 • Quiz next time we meet

Finding Trig Ratios • A trigonometric ratio is a ratio of the lengths of two sides of a right triangle. The word trigonometry is derived from the ancient Greek language and means measurement of triangles. The three basic trigonometric ratios are sine, cosine, and tangent, which are abbreviated as sin, cos, and tan respectively.

Trigonometric Ratios • Let ∆ABC be a right triangle. The since, the cosine, and the tangent of the acute angle A are defined as follows. cos A = Side adjacent to A hypotenuse sin A = Side opposite A hypotenuse = = b c a c tan A = Side opposite A a = Side adjacent to A b

Note: • The value of a trigonometric ratio depends only on the measure of the acute angle, not on the particular right triangle that is used to compute the value.

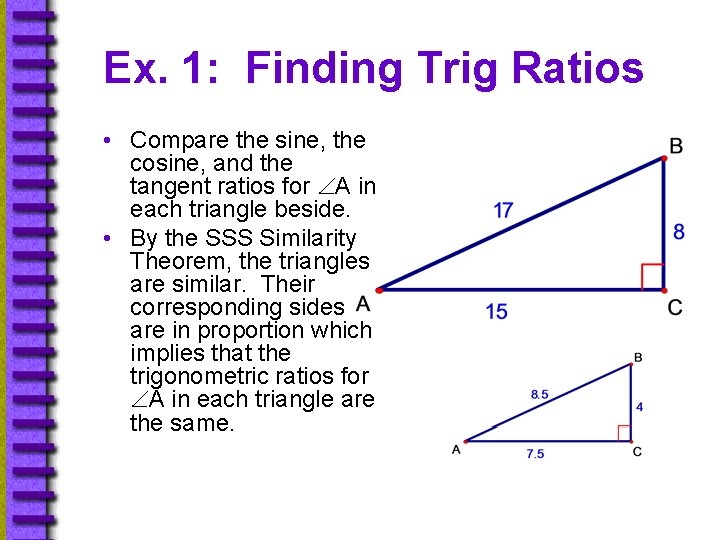
Ex. 1: Finding Trig Ratios • Compare the sine, the cosine, and the tangent ratios for A in each triangle beside. • By the SSS Similarity Theorem, the triangles are similar. Their corresponding sides are in proportion which implies that the trigonometric ratios for A in each triangle are the same.

Ex. 1: Finding Trig Ratios Large sin A = cos. A = tan. A = opposite hypotenuse adjacent hypotenuse opposite adjacent 8 Small ≈ 0. 4706 4 ≈ 0. 4706 8. 5 15 ≈ 0. 8824 17 7. 5 ≈ 0. 8824 8. 5 17 8 ≈ 0. 5333 15 4 ≈ 0. 5333 7. 5 Trig ratios are often expressed as decimal approximations.

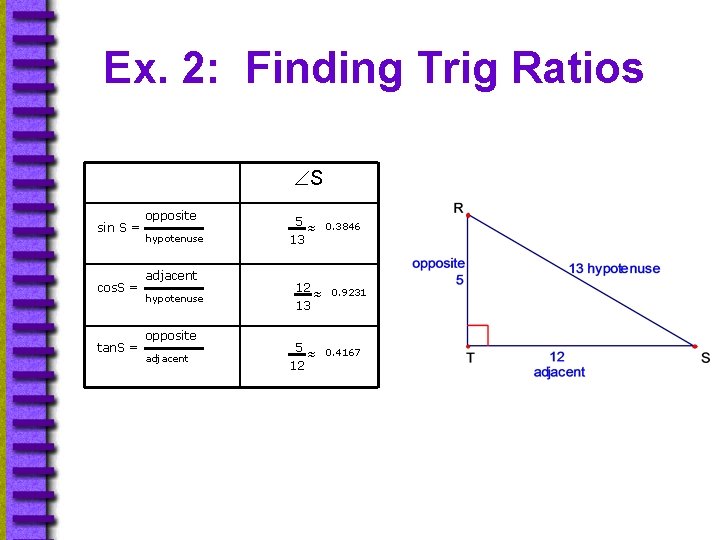
Ex. 2: Finding Trig Ratios S sin S = cos. S = tan. S = opposite hypotenuse adjacent hypotenuse opposite adjacent 5 ≈ 0. 3846 13 12 ≈ 0. 9231 13 5 ≈ 0. 4167 12

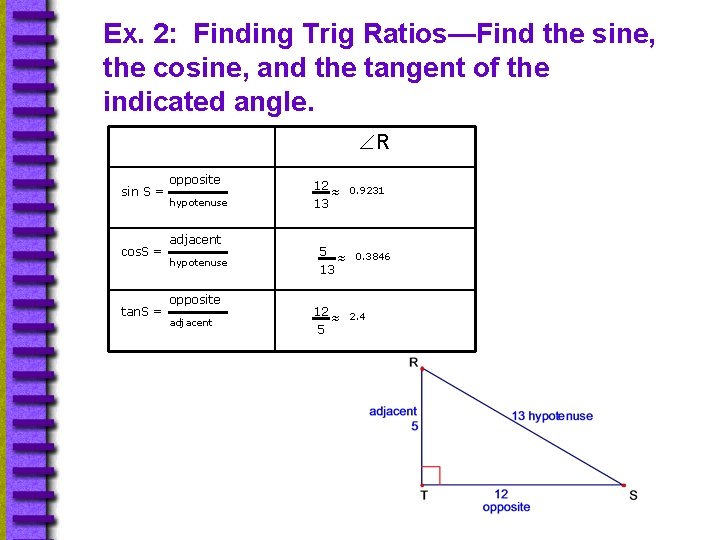
Ex. 2: Finding Trig Ratios—Find the sine, the cosine, and the tangent of the indicated angle. R sin S = cos. S = tan. S = opposite hypotenuse adjacent hypotenuse opposite adjacent 12 ≈ 0. 9231 13 5 13 ≈ 0. 3846 12 ≈ 2. 4 5

Ex. 3: Finding Trig Ratios—Find the sine, the cosine, and the tangent of 45 45 sin 45 = cos 45 = tan 45 = opposite hypotenuse adjacent hypotenuse opposite adjacent 1 √ 2 = = √ 2 2 1 1 ≈ 0. 7071 = 1 Begin by sketching a 45 -90 triangle. Because all such triangles are similar, you can make calculations simple by choosing 1 as the length of each leg. From Theorem 9. 8 on page 551, it follows that the length of the hypotenuse is √ 2 45

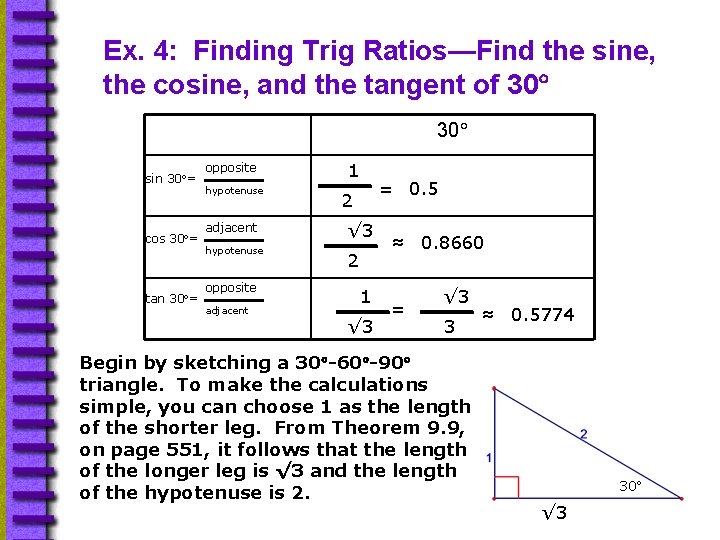
Ex. 4: Finding Trig Ratios—Find the sine, the cosine, and the tangent of 30 30 sin 30 = cos 30 = tan 30 = opposite hypotenuse adjacent hypotenuse opposite adjacent 1 = 0. 5 2 √ 3 2 1 √ 3 ≈ 0. 8660 = √ 3 3 Begin by sketching a 30 -60 -90 triangle. To make the calculations simple, you can choose 1 as the length of the shorter leg. From Theorem 9. 9, on page 551, it follows that the length of the longer leg is √ 3 and the length of the hypotenuse is 2. ≈ 0. 5774 30 √ 3

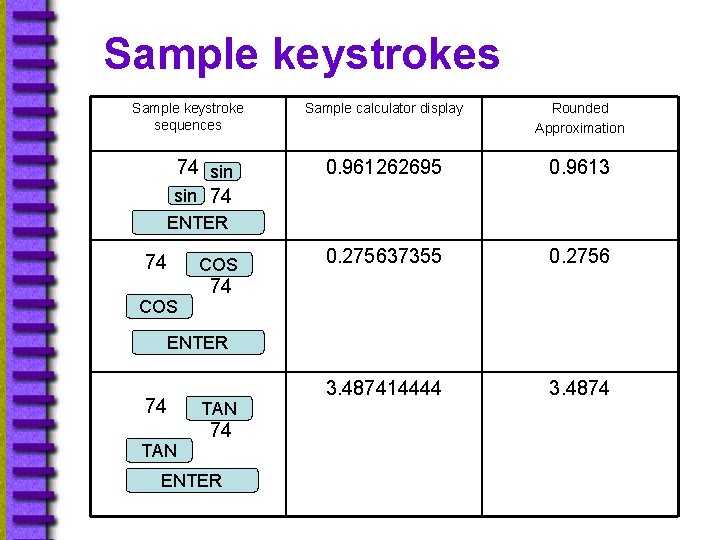
Ex: 5 Using a Calculator • You can use a calculator to approximate the sine, cosine, and the tangent of 74. Make sure that your calculator is in degree mode. The table shows some sample keystroke sequences accepted by most calculators.

Sample keystrokes Sample keystroke sequences 74 sin 74 Sample calculator display Rounded Approximation 0. 961262695 0. 9613 0. 275637355 0. 2756 3. 487414444 3. 4874 ENTER 74 COS 74 ENTER 74 TAN 74 ENTER

Notes: • If you look back at Examples 1 -5, you will notice that the sine or the cosine of an acute triangles is always less than 1. The reason is that these trigonometric ratios involve the ratio of a leg of a right triangle to the hypotenuse. The length of a leg or a right triangle is always less than the length of its hypotenuse, so the ratio of these lengths is always less than one.

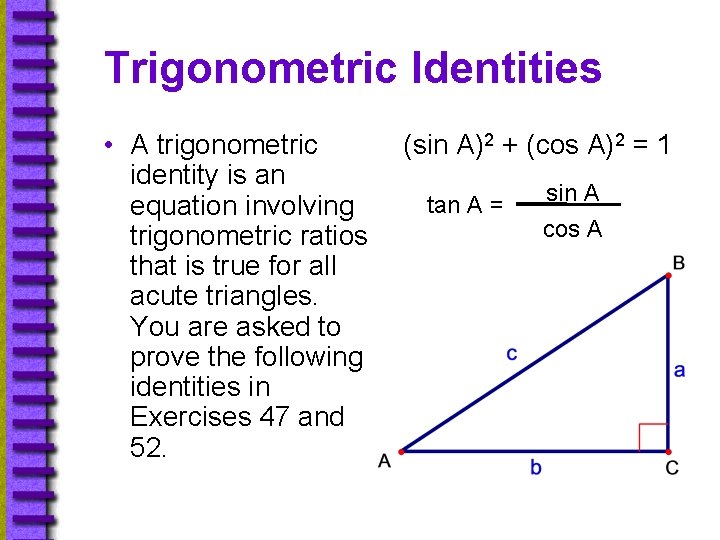
Trigonometric Identities • A trigonometric identity is an equation involving trigonometric ratios that is true for all acute triangles. You are asked to prove the following identities in Exercises 47 and 52. (sin A)2 + (cos A)2 = 1 tan A = sin A cos A

Using Trigonometric Ratios in Real-life • Suppose you stand look up at a point in the distance. Maybe you are looking up at the top of a tree as in Example 6. The angle that your line of sight makes with a line drawn horizontally is called angle of elevation.

Ex. 6: Indirect Measurement • You are measuring the height of a Sitka spruce tree in Alaska. You stand 45 feet from the base of the tree. You measure the angle of elevation from a point on the ground to the top of the tree to be 59°. To estimate the height of the tree, you can write a trigonometric ratio that involves the height h and the known length of 45 feet.

The math tan 59° = opposite Write the ratio adjacent tan 59° = h Substitute values 45 45 tan 59° = h Multiply each side by 45 45 (1. 6643) ≈ h Use a calculator or table to find tan 59° 75. 9 ≈ h Simplify The tree is about 76 feet tall.

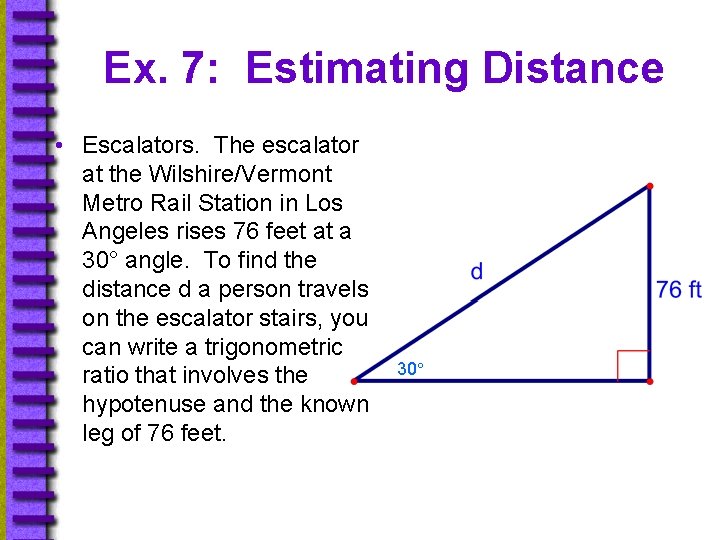
Ex. 7: Estimating Distance • Escalators. The escalator at the Wilshire/Vermont Metro Rail Station in Los Angeles rises 76 feet at a 30° angle. To find the distance d a person travels on the escalator stairs, you can write a trigonometric ratio that involves the hypotenuse and the known leg of 76 feet. 30°

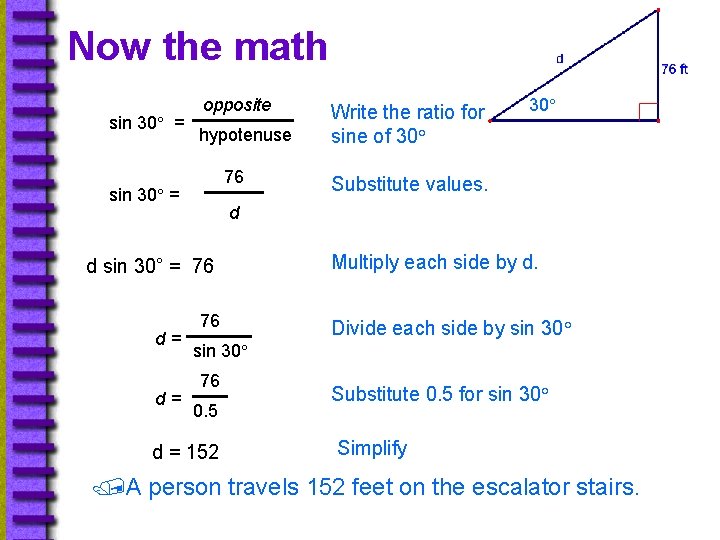
Now the math sin 30° = opposite hypotenuse 76 sin 30° = d= 30° Substitute values. d d sin 30° = 76 d= Write the ratio for sine of 30° 76 Multiply each side by d. Divide each side by sin 30° 76 0. 5 d = 152 Substitute 0. 5 for sin 30° Simplify A person travels 152 feet on the escalator stairs.

Reminders: • After this section, you have a quiz on Thursday or Friday. • Chapter 9 exam will take place before you leave for spring break. . . Take it before you go on break. • Binder check before spring break. These are your new grades for the last quarter of the year. Study and don’t slack off now.