9 5 Solving by Factoring Algebra 14 0

9. 5 Solving by Factoring Algebra 14. 0, 23. 0

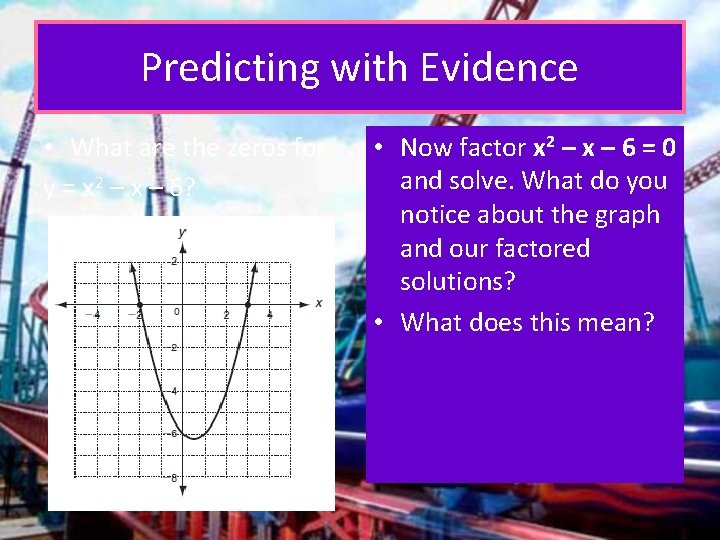
Predicting with Evidence • What are the zeros for y = x 2 – x – 6? • Now factor x 2 – x – 6 = 0 and solve. What do you notice about the graph and our factored solutions? • What does this mean?

Main Idea • For the rest of the chapter, we are going to learn different methods to solve a quadratic equation, besides graphing. • Instead of graphing a parabola to find the zeros, we are going to learn ways to find the zeros, which are solutions. • Today, we are going to use our chapter 8 skills to factor a quadratic equation. By breaking it down, we can find the zeros!

Zero Product Property • Zero Product Property: if the product equals zero, then one of the values must equal zero. • This property helps to find our ZEROS. • Meaning: Our quadratic equation must equal 0 in order to find the zeros by solving.

Ex 1 -Using the Zero Product Property • These quadratic equations are already factored, so finish by setting each factor equal to 0 and solve.

Practice 1

Example 2: Solving by Factoring • Solving by factoring: 1) Write the quadratic equation in standard form: y = ax 2 + bx + c OR ax 2 + bx + c = 0 2) Factor the quadratic equation (chapter 8) 3) Use the Zero Product Property to set each factor to 0 and solve. The answers are your zeros on the graph!

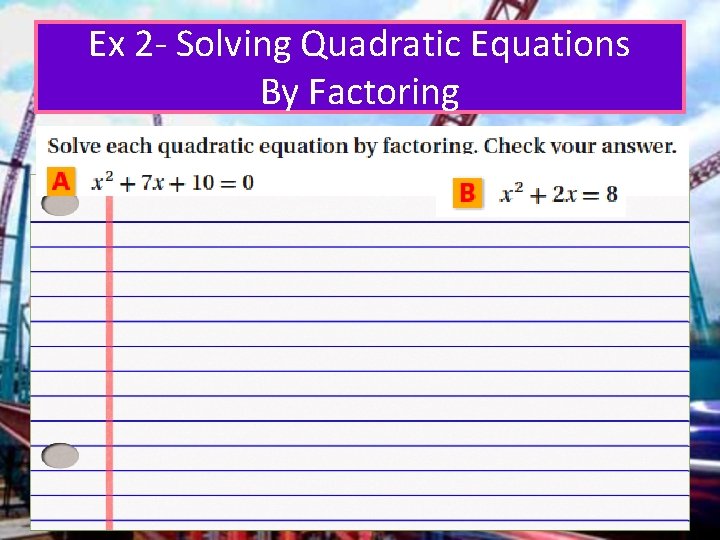
Ex 2 - Solving Quadratic Equations By Factoring

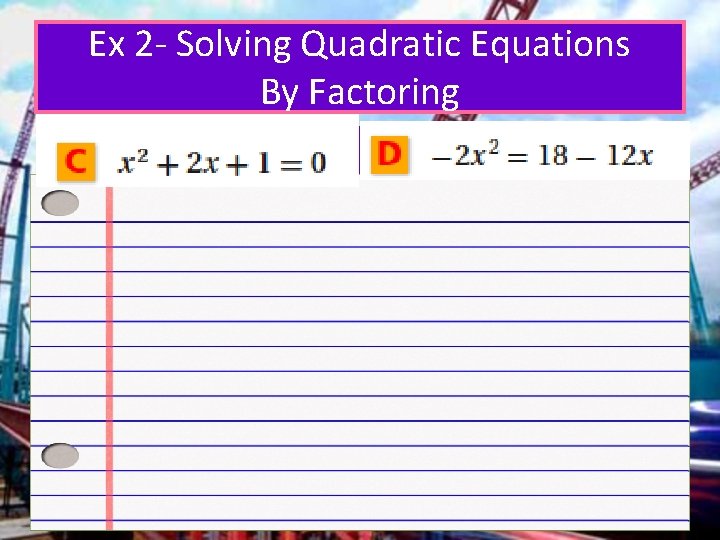
Ex 2 - Solving Quadratic Equations By Factoring

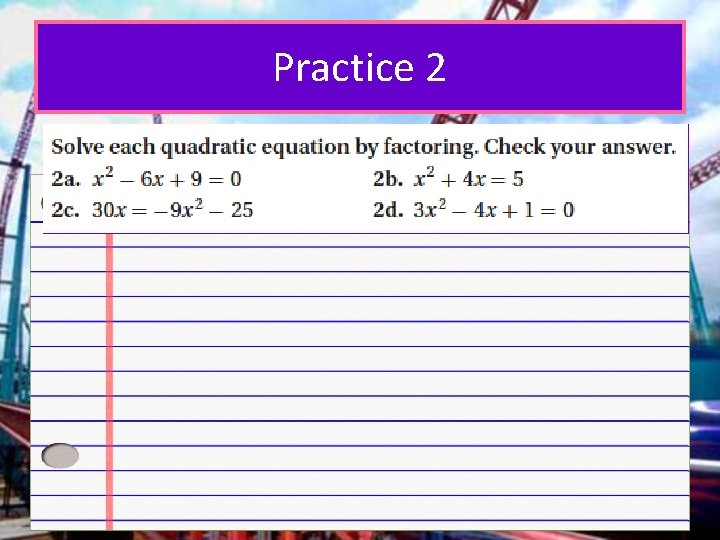
Practice 2

Ex 3 Sports Application Same steps: 1) Write in standard form 2) Factor 3) Solve each factor to find the zeros!

Practice 3

Review • What are you trying to find when you graph or solve quadratic equations? • What is the zero product property? How does it help you solve? • How do you know if your solutions are correct?