9 4 Radius of Convergence Convergence The series












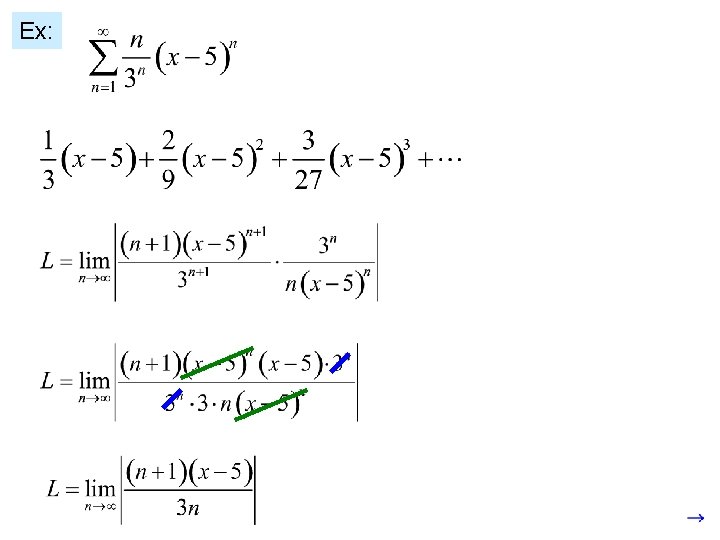




- Slides: 17

9. 4 Radius of Convergence

Convergence The series that are of the most interest to us are those that converge. Today we will consider the question: “Does this series converge, and if so, for what values of x does it converge? ”

The first requirement of convergence is that the terms must approach zero. nth term test for divergence diverges if fails to exist or is not zero. Ex. Note 2: that this can prove If that athen grows without series diverges, but can not prove that a series converges. bound. If As then , eventually is larger than , therefore The series diverges. (except when x=0) the numerator grows faster than the denominator.

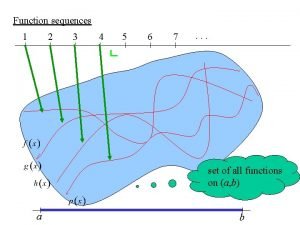
There are three possibilities for power series convergence. 1 The series converges over some finite interval: (the interval of convergence). There is a positive number R such that the series diverges for but converges for . The series may or may not converge at the endpoints of the interval. 2 The series converges for every x. ( 3 The series converges at everywhere else. ( ) and diverges ) (As in the previous example. ) The number R is the radius of convergence.

Direct Comparison Test For non-negative series: If every term of a series is less than the corresponding term of a convergent series, then both series converge. If every term of a series is greater than the corresponding term of a divergent series, then both series diverge. This series converges. So this series must also converge. So this series must also diverge. This series diverges.

Ex. 3: Prove that converges for all real x. There are no negative terms: larger denominator is the Taylor series for , which converges. The original series converges. The direct comparison test only works when the terms are non-negative.

Absolute Convergence If converges, then we say converges absolutely. The term “converges absolutely” means that the series formed the absolute value of each term If by taking converges, then converges. Sometimes in the English language we use the word “absolutely” to mean “really” or “actually”. This is If the series not the caseformed here! by taking the absolute value of each term converges, then the original series must also converge. “If a series converges absolutely, then it converges. ”

Ex. 4: We test for absolute convergence: Since , converges to converges by the direct comparison test. Since converges absolutely, it converges.

Ratio Technique We have learned that the partial sum of a geometric series is given by: where r = common ratio between terms When , the series converges.

Geometric series have a constant ratio between terms. Other series have ratios that are not constant. If the absolute value of the limit of the ratio between consecutive terms is less than one, then the series will converge. For , if then: if the series converges. if the series diverges. if the series may or may not converge.

Ex: If we replace x with x-1, we get: If the limit of the ratio between consecutive terms is less than one, then the series will converge.

If the limit of the ratio between consecutive terms is less than one, then the series will converge. The interval of convergence is (0, 2). The radius of convergence is 1.
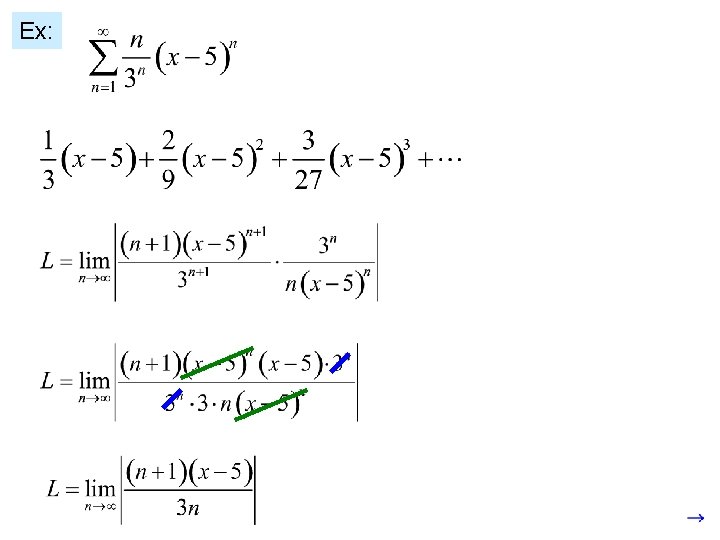
Ex:

Ex: The interval of convergence is (2, 8). The radius of convergence is .

Ex:

Ex: for all At , the series is . Radius of convergence = 0. , which converges to zero. Note: If R is infinite, then the series converges for all values of x.

Another series for which it is easy to find the sum is the telescoping series. Ex. 6: Using partial fractions: Telescoping Series converges to p
 Maclaurin series radius of convergence
Maclaurin series radius of convergence Atomic size in periodic table
Atomic size in periodic table Interval of convergence
Interval of convergence Radius of convergence
Radius of convergence Converges conditionally
Converges conditionally Uniform convergence of series
Uniform convergence of series The test for divergence
The test for divergence Uniform convergence of series
Uniform convergence of series Divergent convergent
Divergent convergent Uniform convergence of series
Uniform convergence of series Uniform convergence of series examples
Uniform convergence of series examples Geometric series
Geometric series Heisenberg 1925 paper
Heisenberg 1925 paper Series aiding and series opposing
Series aiding and series opposing Taylor series lesson
Taylor series lesson Taylor series of composite functions
Taylor series of composite functions Arithmetic series vs geometric series
Arithmetic series vs geometric series Ibm p series server
Ibm p series server