9 4 Perimeter and Area in the Coordinate

9 -4 Perimeter and Area in the Coordinate Plane Warm Up Use the slope formula to determine the slope of each line. 1. 2. 3. Simplify Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Holt Geometry

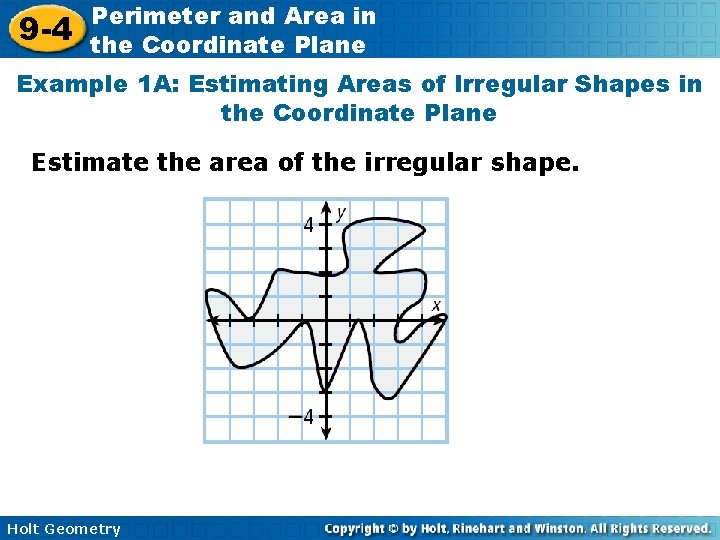
9 -4 Perimeter and Area in the Coordinate Plane Example 1 A: Estimating Areas of Irregular Shapes in the Coordinate Plane Estimate the area of the irregular shape. Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Example 1 A Continued Method 1: Draw a composite figure that approximates the irregular shape and find the area of the composite figure. The area is approximately 4 + 5. 5 + 2 + 3 + 4 + 1. 5 + 1 + 6 = 30 units 2. Holt Geometry

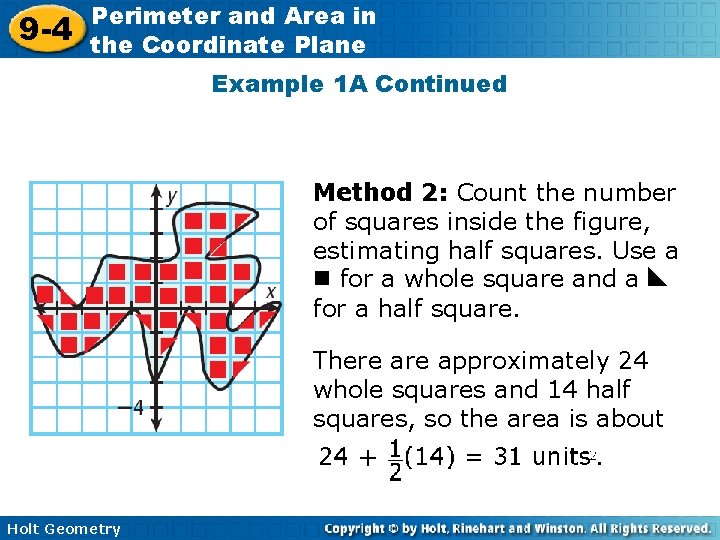
9 -4 Perimeter and Area in the Coordinate Plane Example 1 A Continued Method 2: Count the number of squares inside the figure, estimating half squares. Use a for a whole square and a for a half square. There approximately 24 whole squares and 14 half squares, so the area is about Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Check It Out! Example 1 Estimate the area of the irregular shape. There approximately 33 whole squares and 9 half squares, so the area is about 38 units 2. Holt Geometry

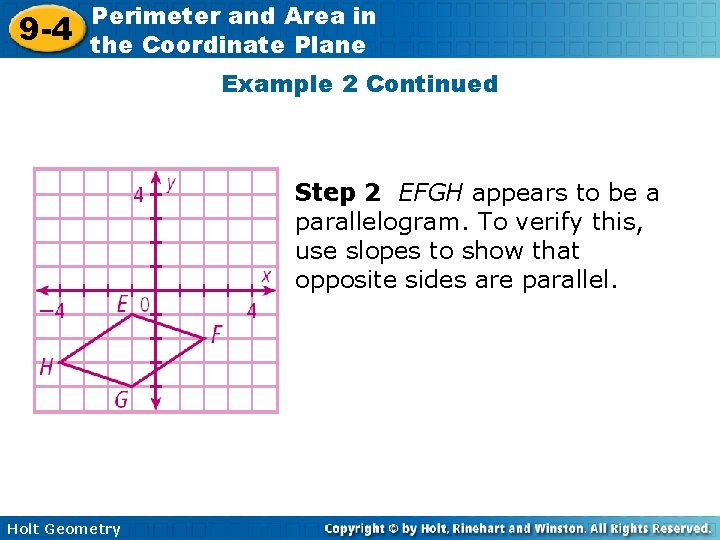
9 -4 Perimeter and Area in the Coordinate Plane Example 2: Finding Perimeter and Area in the Coordinate Plane Draw and classify the polygon with vertices E( – 1, – 1), F(2, – 2), G(– 1, – 4), and H(– 4, – 3). Find the perimeter and area of the polygon. Step 1 Draw the polygon. Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Example 2 Continued Step 2 EFGH appears to be a parallelogram. To verify this, use slopes to show that opposite sides are parallel. Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Example 2 Continued slope of EF = slope of GH = slope of FG = slope of HE = Holt Geometry The opposite sides are parallel, so EFGH is a parallelogram.

9 -4 Perimeter and Area in the Coordinate Plane Example 2 Continued Step 3 Since EFGH is a parallelogram, EF = GH, and FG = HE. Use the Distance Formula to find each side length. perimeter of EFGH: Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Example 2 Continued To find the area of EFGH, draw a line to divide EFGH into two triangles. The base and height of each triangle is 3. The area of each triangle is The area of EFGH is 2(4. 5) = 9 units 2. Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Check It Out! Example 2 Continued To find the area of HJKL, draw a line to divide HJKL into two triangles. The base and height of each triangle is 3. The area of each triangle is The area of HJKL is 2(12. 5) = 25 units 2. Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Check It Out! Example 3 Find the area of the polygon with vertices K(– 2, 4), L(6, – 2), M(4, – 4), and N(– 6, – 2). Draw the polygon and close it in a rectangle. Area of rectangle: A = bh = 12(8)= 96 units 2. Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Check It Out! Example 3 Continued Area of triangles: a d b c The area of the polygon is 96 – 12 – 24 – 2 – 10 = 48 units 2. Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane P 619 #2 -8 evens Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Lesson Quiz: Part I 1. Estimate the area of the irregular shape. 25. 5 units 2 2. Draw and classify the polygon with vertices L(– 2, 1), M(– 2, 3), N(0, 3), and P(1, 0). Find the perimeter and area of the polygon. Kite; P = 4 + 2√ 10 units; A = 6 units 2 Holt Geometry

9 -4 Perimeter and Area in the Coordinate Plane Lesson Quiz: Part II 3. Find the area of the polygon with vertices S(– 1, – 1), T(– 2, 1), V(3, 2), and W(2, – 2). A = 12 units 2 4. Show that the two composite figures cover the same area. For both figures, A = 3 + 1 + 2 = 6 units 2. Holt Geometry