9 3 Rotations Warm Up Lesson Presentation Lesson

9 -3 Rotations Warm Up Lesson Presentation Lesson Quiz Holt. Mc. Dougal Geometry Holt

9 -3 Rotations Warm Up 1. The translation image of P(– 3, – 1) is P’(1, 3). Find the translation image of Q(2, – 4). Q’(6, 0) Holt Mc. Dougal Geometry

9 -3 Rotations Objective Identify and draw rotations. Holt Mc. Dougal Geometry

9 -3 Rotations COPY THIS SLIDE: A rotation is a transformation that turns a figure around a fixed point, called the center of rotation. A rotation is an isometry, so the image of a rotated figure is congruent to the preimage. Holt Mc. Dougal Geometry

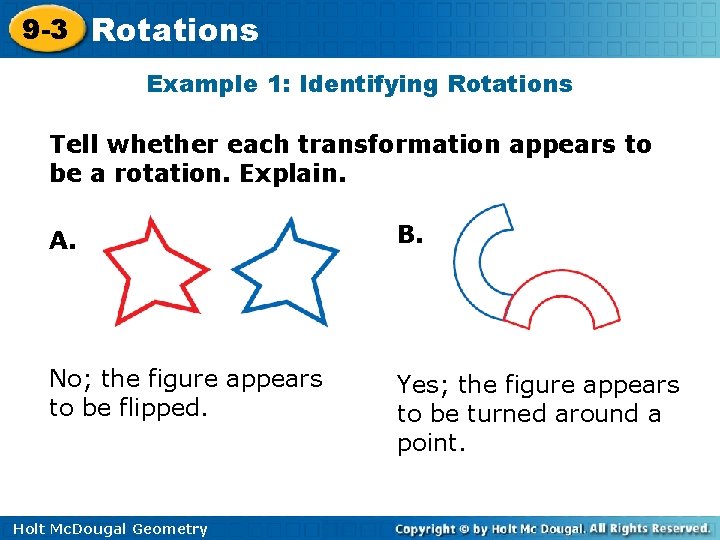
9 -3 Rotations Example 1: Identifying Rotations Tell whether each transformation appears to be a rotation. Explain. A. B. No; the figure appears to be flipped. Yes; the figure appears to be turned around a point. Holt Mc. Dougal Geometry

9 -3 Rotations Check It Out! Example 1 COPY THIS SLIDE: Tell whether each transformation appears to be a rotation. b. a. No, the figure appears to be a translation. Holt Mc. Dougal Geometry Yes, the figure appears to be turned around a point.

9 -3 Rotations COPY THIS SLIDE: Holt Mc. Dougal Geometry

9 -3 Rotations Helpful Hint Unless otherwise stated, all rotations in this book are counterclockwise. Holt Mc. Dougal Geometry

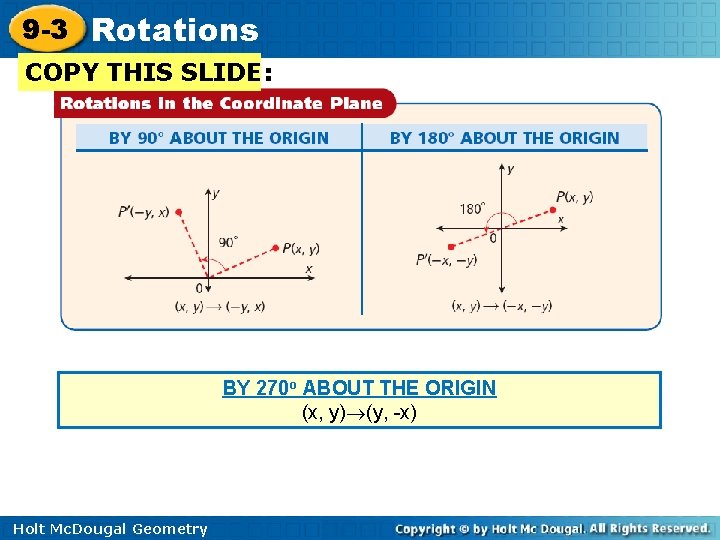
9 -3 Rotations COPY THIS SLIDE: BY 270 o ABOUT THE ORIGIN (x, y) (y, -x) Holt Mc. Dougal Geometry

9 -3 Rotations Example 3: Drawing Rotations in the Coordinate Plane COPY THIS SLIDE: Rotate ΔJKL with vertices J(2, 2), K(4, – 5), and L(– 1, 6) by 180° about the origin. The rotation of (x, y) is (–x, –y). J(2, 2) J’(– 2, – 2) K(4, – 5) K’(– 4, 5) L(– 1, 6) L’(1, – 6) Graph the preimage and image. Holt Mc. Dougal Geometry

9 -3 Rotations Check It Out! Example 3 COPY THIS SLIDE: Rotate ∆ABC by 180° about the origin. The rotation of (x, y) is (–x, –y). A(2, – 1) A’(– 2, 1) B(4, 1) B’(– 4, – 1) C(3, 3) C’(– 3, – 3) Graph the preimage and image. Holt Mc. Dougal Geometry

9 -3 Rotations COPY THIS SLIDE: Examples: Rotate ∆RST with vertices R(– 1, 4), S(2, 1), and T(3, – 3) about the origin by the given angle. 1. 90° R’(– 4, – 1), S’(– 1, 2), T’(3, 3) 2. 180° R’(1, – 4), S’(– 2, – 1), T’(– 3, 3) 3. 270° R’(4, 1), S’(1, – 2), T’(– 3, – 3) Holt Mc. Dougal Geometry

9 -3 Rotations Classwork/Homework • 9. 3 W/S Holt Mc. Dougal Geometry