9 3 Arithmetic Sequences and Series Objectives Find

9 -3 Arithmetic Sequences and Series Objectives Find the indicated terms of an arithmetic sequence. Find the sums of arithmetic series. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Vocabulary arithmetic sequence arithmetic series Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series The cost of mailing a letter in 2005 gives the sequence 0. 37, 0. 60, 0. 83, 1. 06, …. This sequence is called an arithmetic sequence because its successive terms differ by the same number d (d ≠ 0), called the common difference. For the mail costs, d is 0. 23, as shown. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Recall that linear functions have a constant first difference. Notice also that when you graph the ordered pairs (n, an) of an arithmetic sequence, the points lie on a straight line. Thus, you can think of an arithmetic sequence as a linear function with sequential natural numbers as the domain. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 1 A: Identifying Arithmetic Sequences Determine whether the sequence could be arithmetic. If so, find the common first difference and the next term. – 10, – 4, 2, 8, 14, … – 10, Differences – 4, 6 2, 6 8, 6 14 6 The sequence could be arithmetic with a common difference of 6. The next term is 14 + 6 = 20. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 1 B: Identifying Arithmetic Sequences Determine whether the sequence could be arithmetic. If so, find the common first difference and the next term. – 2, – 5, – 11, – 20, – 32, … – 2, Differences – 5, – 3 – 11, – 6 – 20, – 32 – 9 – 12 The sequence is not arithmetic because the first differences are not common. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 1 a Determine whether the sequence could be arithmetic. If so, find the common difference and the next term. 1. 9, 1. 2, 0. 5, – 0. 2, – 0. 9, . . . 1. 9, Differences 1. 2, – 0. 7 0. 5, – 0. 7 – 0. 2, – 0. 7 – 0. 9 – 0. 7 The sequence could be arithmetic with a common difference of – 0. 7. The next term would be – 0. 9 – 0. 7 = – 1. 6. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 1 b Determine whether the sequence could be arithmetic. If so, find the common difference and the next term. Differences The sequence is not arithmetic because the first differences are not common. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Each term in an arithmetic sequence is the sum of the previous term and the common difference. This gives the recursive rule an = an – 1 + d. You also can develop an explicit rule for an arithmetic sequence. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Notice the pattern in the table. Each term is the sum of the first term and a multiple of the common difference. This pattern can be generalized into a rule for all arithmetic sequences. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 2: Finding the nth Term Given an Arithmetic Sequence Find the 12 th term of the arithmetic sequence 20, 14, 8, 2, 4, . . Step 1 Find the common difference: d = 14 – 20 = – 6. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 2 Continued Step 2 Evaluate by using the formula. an = a 1 + (n – 1)d a 12 General rule. = 20 + (12 – 1)(– 6) Substitute 20 for a 1, 12 for n, and – 6 for d. = – 46 The 12 th term is – 46. Check Continue the sequence. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 2 a Find the 11 th term of the arithmetic sequence. – 3, – 5, – 7, – 9, … Step 1 Find the common difference: d = – 5 – (– 3)= – 2. Step 2 Evaluate by using the formula. an = a 1 + (n – 1)d General rule. a 11= – 3 + (11 – 1)(– 2) = – 23 The 11 th term is – 23. Holt Mc. Dougal Algebra 2 Substitute – 3 for a 1, 11 for n, and – 2 for d.

9 -3 Arithmetic Sequences and Series Check It Out! Example 2 a Continued Check Continue the sequence. n 1 2 3 4 5 6 7 8 9 10 11 an – 3 – 5 – 7 – 9 – 11 – 13 – 15 – 17 – 19 – 21 – 23 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 2 b Find the 11 th term of the arithmetic sequence. 9. 2, 9. 15, 9. 1, 9. 05, … Step 1 Find the common difference: d = 9. 15 – 9. 2 = – 0. 05. Step 2 Evaluate by using the formula. an = a 1 + (n – 1)d General rule. a 11= 9. 2 + (11 – 1)(– 0. 05) Substitute 9. 2 for a 1, 11 for n, and – 0. 05 for d. = 8. 7 The 11 th term is 8. 7. Holt Mc. Dougal Algebra 2

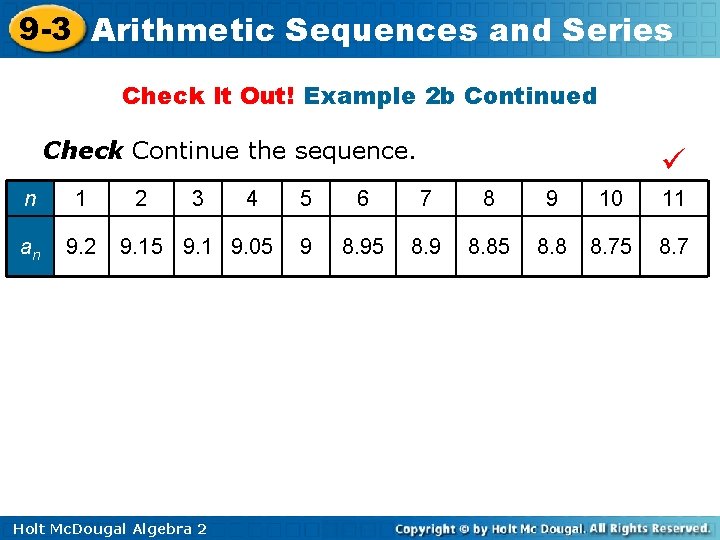
9 -3 Arithmetic Sequences and Series Check It Out! Example 2 b Continued Check Continue the sequence. n 1 an 9. 2 2 3 4 9. 15 9. 1 9. 05 Holt Mc. Dougal Algebra 2 5 6 7 8 9 10 11 9 8. 95 8. 9 8. 85 8. 8 8. 75 8. 7

9 -3 Arithmetic Sequences and Series Example 3: Finding Missing Terms Find the missing terms in the arithmetic sequence 17, , – 7. Step 1 Find the common difference. an = a 1 + (n – 1)d General rule. – 7 = 17 + (5 – 1)(d) Substitute – 7 for an, 17 for a 1, and 5 for n. – 6 = d Solve for d. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 3 Continued Step 2 Find the missing terms using d= – 6 and a 1 = 17. a 2 = 17 + (2 – 1)(– 6) = 11 a 3 = 17 +(3 – 1)(– 6) =5 a 4 = 17 + (4 – 1)(– 6) = – 1 Holt Mc. Dougal Algebra 2 The missing terms are 11, 5, and – 1.

9 -3 Arithmetic Sequences and Series Check It Out! Example 3 Find the missing terms in the arithmetic sequence 2, , 0. Step 1 Find the common difference. an = a 1 + (n – 1)d 0 = 2 + (5 – 1)d – 2 = 4 d General rule. Substitute 0 for an, 2 for a 1, and 5 for n. Solve for d. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 3 Continued Step 2 Find the missing terms using d= and a 1= 2. The missing terms are =1 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Because arithmetic sequences have a common difference, you can use any two terms to find the difference. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 4: Finding the nth Term Given Two Terms Find the 5 th term of the arithmetic sequence with a 8 = 85 and a 14 = 157. Step 1 Find the common difference. an = a 1 + (n – 1)d a 14 = a 8 + (14 – 8)d Let an = a 14 and a 1 = a 8. Replace 1 with 8. a 14 = a 8 + 6 d Simplify. 157 = 85 + 6 d 72 = 6 d 12 = d Holt Mc. Dougal Algebra 2 Substitute 157 for a 14 and 85 for a 8.

9 -3 Arithmetic Sequences and Series Example 4 Continued Step 2 Find a 1. an = a 1 + (n – 1)d General rule 85 = a 1 + (8 - 1)(12) Substitute 85 for a 8, 8 for n, and 12 for d. 85 = a 1 + 84 Simplify. 1 = a 1 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 4 Continued Step 3 Write a rule for the sequence, and evaluate to find a 5. an = a 1 + (n – 1)d General rule. an = 1 + (n – 1)(12) Substitute 1 for a 1 and 12 for d. a 5 = 1 + (5 – 1)(12) Evaluate for n = 5. = 49 The 5 th term is 49. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 4 a Find the 11 th term of the arithmetic sequence. a 2 = – 133 and a 3 = – 121 Step 1 Find the common difference. an = a 1 + (n – 1)d a 3 = a 2 + (3 – 2)d Let an = a 3 and a 1 = a 2. Replace 1 with 2. a 3 = a 2 + d – 121 = – 133 + d d = 12 Holt Mc. Dougal Algebra 2 Simplify. Substitute – 121 for a 3 and – 133 for a 2.

9 -3 Arithmetic Sequences and Series Check It Out! Example 4 a Continued Step 2 Find a 1. an = a 1 + (n – 1)d General rule Substitute – 133 for an, 2 for n, – 133 = a 1 + (2 – 1)(12) and 12 for d. – 133 = a 1 + 12 – 145 = a 1 Holt Mc. Dougal Algebra 2 Simplify.

9 -3 Arithmetic Sequences and Series Check It Out! Example 4 a Continued Step 3 Write a rule for the sequence, and evaluate to find a 11. an = a 1 + (n – 1)d General rule. a 11 = – 145 + (n – 1)(12) Substitute – 145 for a 1 and 12 for d. a 11 = – 145 + (11 – 1)(12) Evaluate for n = 11. = – 25 The 11 th term is – 25. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 4 b Find the 11 th term of each arithmetic sequence. a 3 = 20. 5 and a 8 = 13 Step 1 Find the common difference. an = a 1 + (n – 1)d a 8 = a 3 + (8 – 3)d General rule Let an = a 8 and a 1 = a 3. Replace 1 with 3. a 8 = a 3 + 5 d Simplify. 13 = 20. 5 + 5 d Substitute 13 for a 8 and 20. 5 for a 3. – 7. 5 = 5 d – 1. 5 = d Holt Mc. Dougal Algebra 2 Simplify.

9 -3 Arithmetic Sequences and Series Check It Out! Example 4 b Continued Step 2 Find a 1. an = a 1 + (n – 1)d General rule 20. 5 = a 1 + (3 – 1)(– 1. 5) Substitute 20. 5 for an, 3 for n, and – 1. 5 for d. 20. 5 = a 1 – 3 Simplify. 23. 5 = a 1 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 4 b Continued Step 3 Write a rule for the sequence, and evaluate to find a 11. an = a 1 + (n – 1)d a 11 = 23. 5 + (n – 1)(– 1. 5) a 11 = 23. 5 + (11 – 1)(– 1. 5) a 11 = 8. 5 The 11 th term is 8. 5. Holt Mc. Dougal Algebra 2 General rule Substitute 23. 5 for a 1 and – 1. 5 for d. Evaluate for n = 11.

9 -3 Arithmetic Sequences and Series In Lesson 12 -2 you wrote and evaluated series. An arithmetic series is the indicated sum of the terms of an arithmetic sequence. You can derive a general formula for the sum of an arithmetic series by writing the series in forward and reverse order and adding the results. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 5 A: Finding the Sum of an Arithmetic Series Find the indicated sum for the arithmetic series. S 18 for 13 + 2 + (– 9) + (– 20) +. . . Find the common difference. d = 2 – 13 = – 11 Find the 18 th term. a 18 = 13 + (18 – 1)(– 11) = – 174 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 5 A Continued Sum formula Substitute. = 18(-80. 5) = – 1449 Check Use a graphing calculator. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Remember! These sums are actually partial sums. You cannot find the complete sum of an infinite arithmetic series because the term values increase or decrease indefinitely. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 5 B: Finding the Sum of an Arithmetic Series Find the indicated sum for the arithmetic series. Find S 15. Find 1 st and 15 th terms. a 1 = 5 + 2(1) = 7 a 15 = 5 + 2(15) = 35 = 15(21) = 315 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 5 B Continued Check Use a graphing calculator. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 5 a Find the indicated sum for the arithmetic series. S 16 for 12 + 7 + 2 +(– 3)+ … Find the common difference. d = 7 – 12 = – 5 Find the 16 th term. a 16 = 12 + (16 – 1)(– 5) = – 63 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 5 a Continued Find S 16. Sum formula. Substitute. = 16(– 25. 5) = – 408 Holt Mc. Dougal Algebra 2 Simplify.

9 -3 Arithmetic Sequences and Series Check It Out! Example 5 b Find the indicated sum for the arithmetic series. Find 1 st and 15 th terms. a 1 = 50 – 20(1) = 30 a 15 = 50 – 20(15) = – 250 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 5 b Continued Find S 15. Sum formula. Substitute. = 15(– 110) = – 1650 Holt Mc. Dougal Algebra 2 Simplify.

9 -3 Arithmetic Sequences and Series Example 6 A: Theater Application The center section of a concert hall has 15 seats in the first row and 2 additional seats in each subsequent row. How many seats are in the 20 th row? Write a general rule using a 1 = 15 and d = 2. an = a 1 + (n – 1)d a 20 = 15 + (20 – 1)(2) Explicit rule for nth term Substitute. = 15 + 38 Simplify. = 53 There are 53 seats in the 20 th row. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Example 6 B: Theater Application How many seats in total are in the first 20 rows? Find S 20 using the formula for finding the sum of the first n terms. Formula for first n terms Substitute. Simplify. There are 680 seats in rows 1 through 20. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 6 a What if. . . ? The number of seats in the first row of a theater has 14 seats. Suppose that each row after the first had 2 additional seats. How many seats would be in the 14 th row? Write a general rule using a 1 = 14 and d = 2. an = a 1 + (n – 1)d a 14 = 11 + (14 – 1)(2) = 11 + 26 = 37 Explicit rule for nth term Substitute. Simplify. There are 37 seats in the 14 th row. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Check It Out! Example 6 b How many seats in total are in the first 14 rows? Find S 14 using the formula for finding the sum of the first n terms. Formula for first n terms Substitute. Simplify. There are 336 total seats in rows 1 through 14. Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Lesson Quiz: Part I 1. Determine whether the sequence could be arithmetic. If so, find the first difference and the next term. – 1, – 4, – 7, – 10, – 13, … yes; – 3, – 16 2. Find the 10 th term of the arithmetic sequence – 2, – 5, – 8, – 11, – 14, … – 29 3. Find the missing terms in the arithmetic sequence 15, , 17. 15. 5, 16. 5 4. Find the 6 th term of the arithmetic sequence with a 9 = 64 and a 12 = 88. 40 Holt Mc. Dougal Algebra 2

9 -3 Arithmetic Sequences and Series Lesson Quiz: Part II 5. Find the indicated sum for – 132 6. The side section of an auditorium has 12 seats in the first row and 3 additional seats in each subsequent row. How many seats are in the 10 th row? How many seats in total are in the first 10 rows? 39; 255 Holt Mc. Dougal Algebra 2