9 2 Graph Terminology Special Simple Graphs Complete

9. 2: Graph Terminology

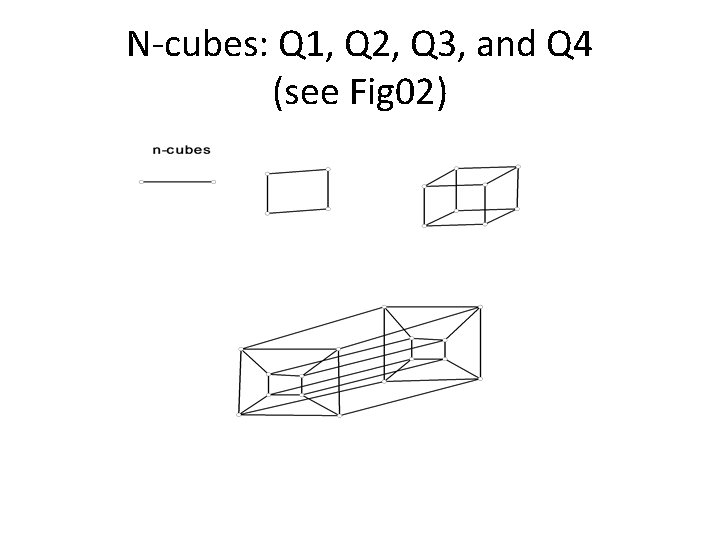
Special Simple Graphs • • • Complete Graphs Cycles Wheels N-cubes Complete bipartite K 1, … C 3, … W 3, … Q 1, … K 2, 2, …

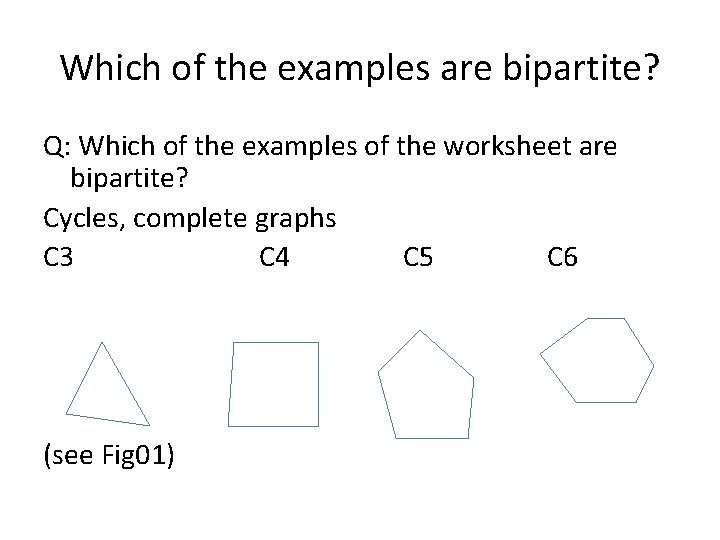
Special Graphs (see Fig 01)

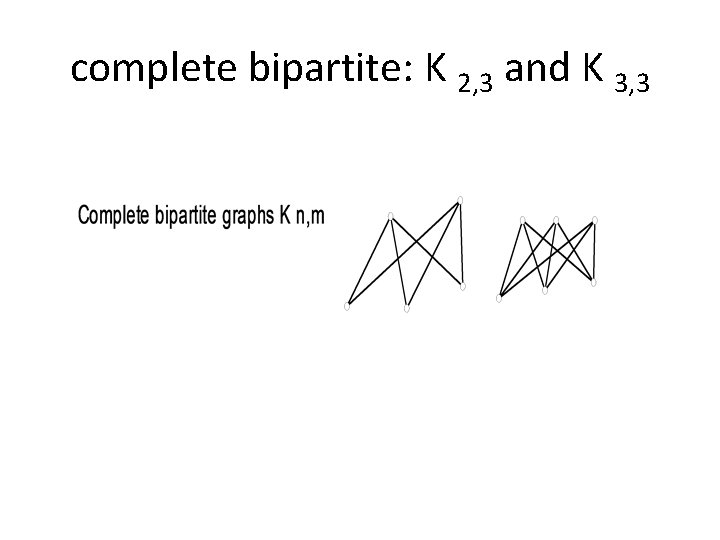
complete bipartite: K 2, 3 and K 3, 3

N-cubes: Q 1, Q 2, Q 3, and Q 4 (see Fig 02)

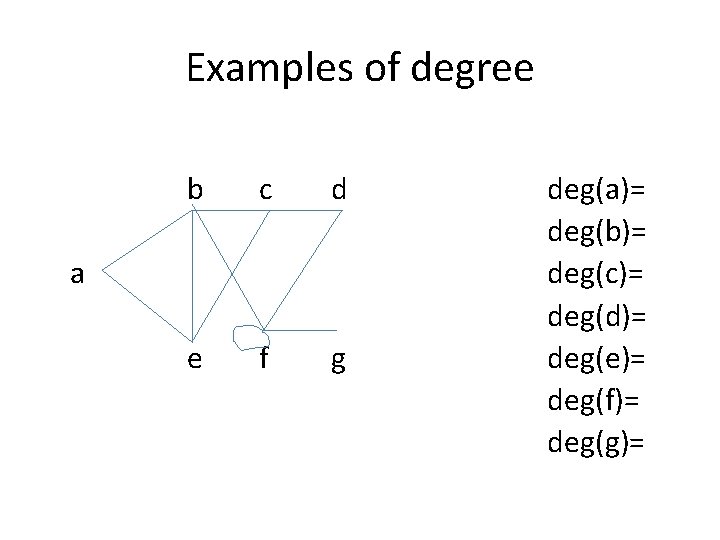
Basic Terminology – Undirected Graphs Def: If e={u, v} is an edge, u and v are adjacent. The edge e is incident with vertices u and v. e connects u and v. The degree of a vertex v, deg(v), is the number of edges incident with it, with loops contributing twice.

Examples of degree b c d e f g a deg(a)= deg(b)= deg(c)= deg(d)= deg(e)= deg(f)= deg(g)=

Theorem 1: The Handshaking Theorem: • Let G=(V, E) be an undirected graph with e edges. • Then = ____

Questions Example: How many edges are there in a graph with 10 vertices each of degree 6? Question: Could you construct a graph with 1 vertex of odd degree?

Questions Could you construct a graph: With 2 vertices of odd degree? With 3, 4, 5, … vertices of odd degree?

Thm. 2: Theorem 2: An undirected graph has an even number of vertices of odd degree. Proof idea: Let V 1 be the set of vertices of odd degree and V 2 be the set of vertices of even degree in the undirected graph G=(V, E). Then, using Thm. 1, ___= = + … Therefore, there an even # of vertices of odd degree.

Directed Graphs- Basic Terms If (u, v) is an edge, u is adjacent to v, and v is adjacent from u u is the initial vertex, and v is the terminal vertex

Deg - (v) and Deg + (v) – Def and Ex Deg - (v) is the in degree of v: the number of edges with v an the terminal vertex Deg + (v) is the out degree of v: the number of edges with v as the initial vertex in out a b c Deg - (a) Deg + (a) Deg - (b) Deg + (b) d e f Deg - (c) Deg + (c) Deg - (d) Deg + (d) Deg - (e) Deg + (e) Deg - (f) Deg + (f)

Thm. 3 Theorem 3: Let G=(V, E) be a graph with directed edges Then = ______ Def: The underlying undirected graph is the undirected graph that results from ignoring directions of edges on a directed graph.

Bipartite Def: A simple graph G is called bipartite if its vertex set V can be partitioned into disjoint nonempty sets V 1 and V 2 such that: If there is an edge between 2 vertices, then one vertex is an element of V 1 and one vertex is an element of V 2.

Which of the examples are bipartite? Q: Which of the examples of the worksheet are bipartite? Cycles, complete graphs C 3 C 4 C 5 C 6 (see Fig 01)

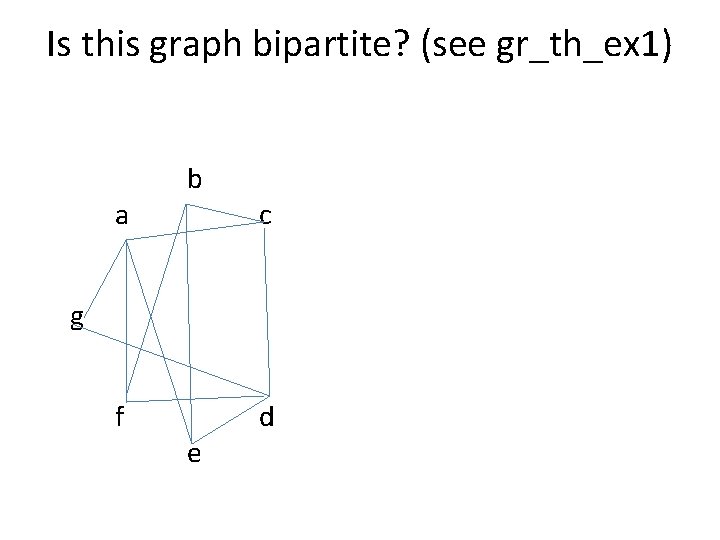
Is this graph bipartite? (see gr_th_ex 1) a b c g f e d

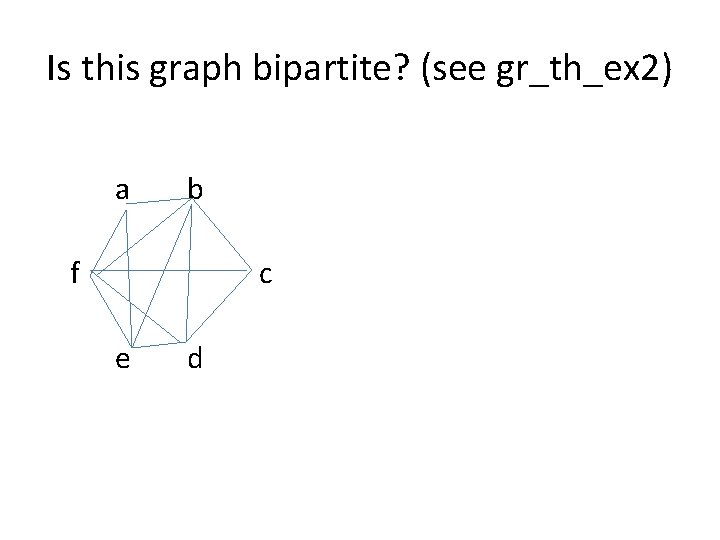
Is this graph bipartite? (see gr_th_ex 2) a b f c e d

Complete Bipartite Graphs Km, n is the graph that is partitioned into two subsets V 1 and V 2 of m and n vertices where There is an edge between two vertices iff one vertex is in V 1 and the other is in V 2. Examples:

Local Area Networks • Star Topology, Ring Topology, Hybrid • Parallel Processing v. Serial

New graphs from old • Def: A subgraph of G=(V, E) is a graph H=(W, F) where W� V and F � E. • Def: The union of two simple graphs G 1=(V 1, E 1) and G 2=(V 2, E 2) is the simple graph G 1� G 2=( V 1 � V 2, E 1 � E 2)