9 1 Developing Formulas for Triangles and Quadrilaterals

9 -1 Developing Formulas for Triangles and Quadrilaterals Warm up Holt Geometry

9 -1 Developing Formulas for Triangles and Quadrilaterals Objectives Develop and apply the formulas for the areas of triangles and special quadrilaterals. Solve problems involving perimeters and areas of triangles and special quadrilaterals. Holt Geometry

9 -1 Developing Formulas for Triangles and Quadrilaterals Remember! The diagonals of a rhombus or kite are perpendicular, and the diagonals of a rhombus bisect each other. Holt Geometry

9 -1 Developing Formulas for Triangles and Quadrilaterals Example 3 A: Finding Measurements of Rhombuses and Kites Find d 2 of a kite in which d 1 = 14 in. and A = 238 in 2. Area of a kite Substitute 238 for A and 14 for d 1. 34 = d 2 Solve for d 2 = 34 Sym. Prop. of = Holt Geometry

9 -1 Developing Formulas for Triangles and Quadrilaterals Example 3 B: Finding Measurements of Rhombuses and Kites Find the area of a rhombus. Area of a rhombus Substitute (8 x+7) for d 1 and (14 x-6) for d 2. . Multiply the binomials (FOIL). Distrib. Prop. Holt Geometry

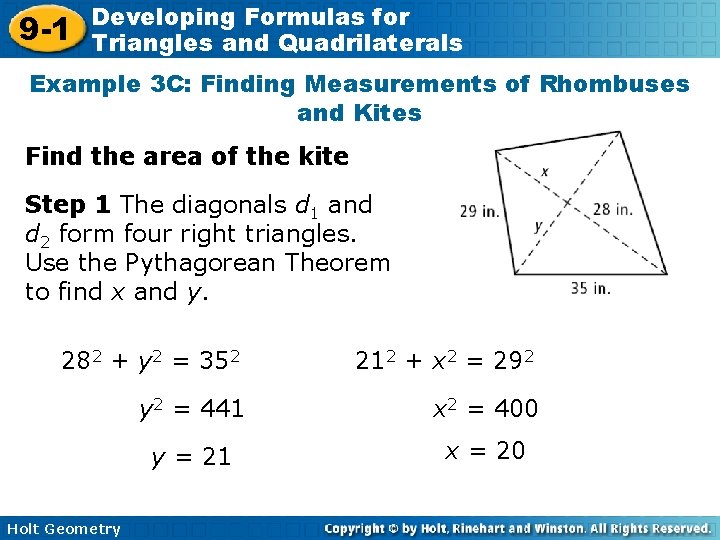
9 -1 Developing Formulas for Triangles and Quadrilaterals Example 3 C: Finding Measurements of Rhombuses and Kites Find the area of the kite Step 1 The diagonals d 1 and d 2 form four right triangles. Use the Pythagorean Theorem to find x and y. 282 + y 2 = 352 212 + x 2 = 292 y 2 = 441 x 2 = 400 y = 21 x = 20 Holt Geometry

9 -1 Developing Formulas for Triangles and Quadrilaterals Example 3 C Continued Step 2 Use d 1 and d 2 to find the area. d 1 is equal to x + 28, which is 48. Half of d 2 is equal to 21, so d 2 is equal to 42. Area of kite Substitute 48 for d 1 and 42 for d 2. A = 1008 in 2 Holt Geometry Simplify.

9 -1 Developing Formulas for Triangles and Quadrilaterals Lesson Quiz: Part II 1. the area of the rhombus A = 1080 m 2 Holt Geometry