8817 Warm Up Solve the inequality 81017 Warm

8/8/17 Warm Up Solve the inequality.

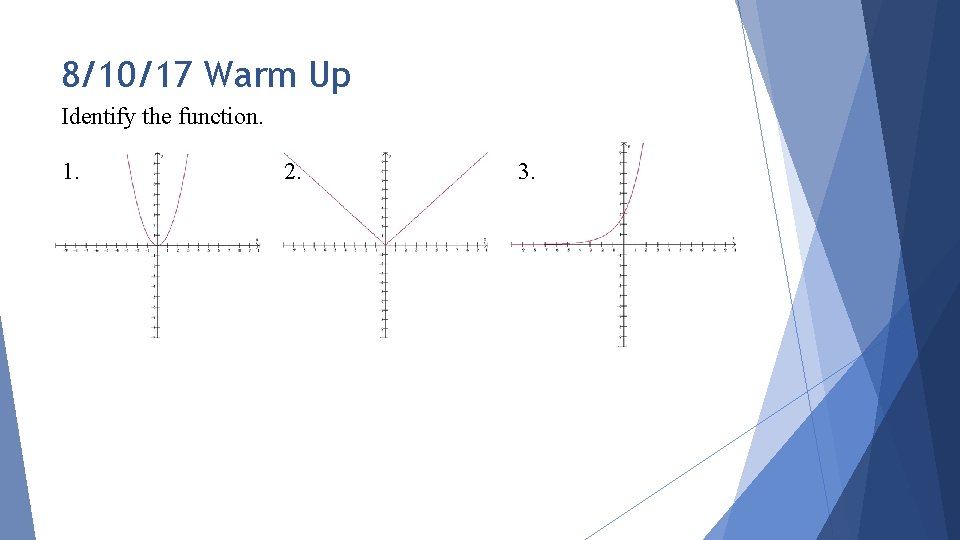
8/10/17 Warm Up Identify the function. 1. 2. 3.

Relations & Functions Domain/Range Parent Functions

Relation A relation is a set of ordered pairs.

Domain and Range The set of input values (x) for a relation is called the domain, and the set of output values (y) is called the range.

Function (vertical line test) a special type of relation in which each element of the domain is paired with exactly one element of the range.

Not a function: The relationship from number to letter is not a function because the domain value 2 is mapped to the range values A, B, and C. Function: The relationship from letter to number is a function because each letter in the domain is mapped to only one number in the range.

Families of Functions or Relations

Polynomial Functions

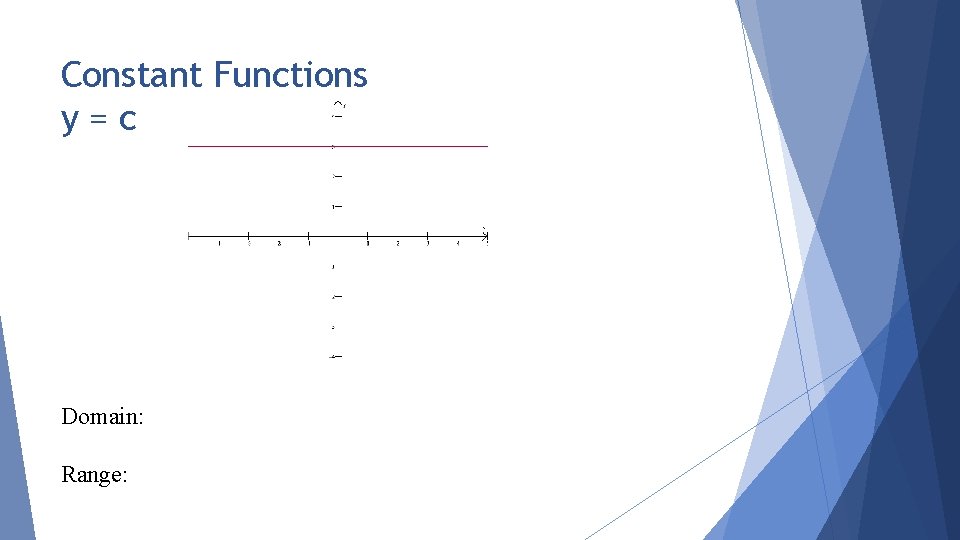
Constant Functions y=c Domain: Range:

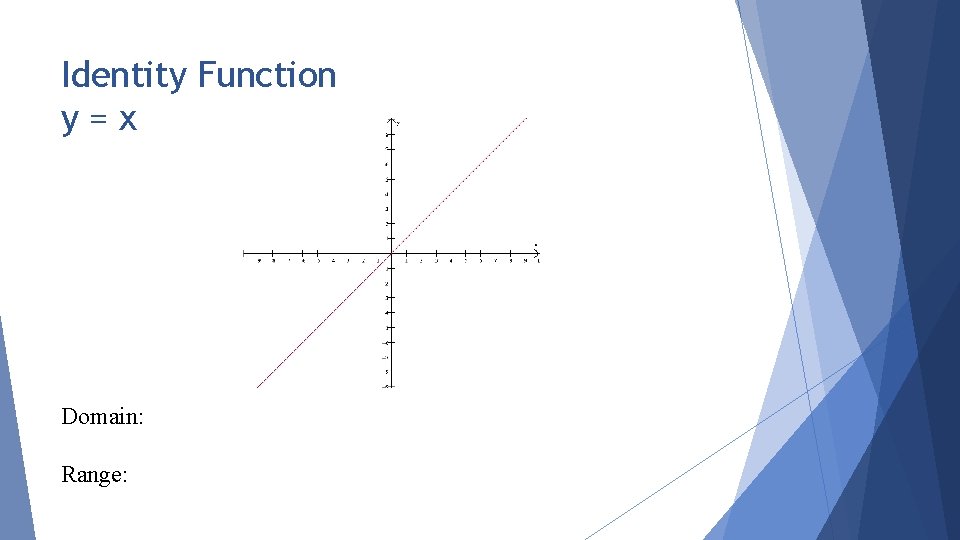
Identity Function y=x Domain: Range:

Linear Functions Domain: Range:

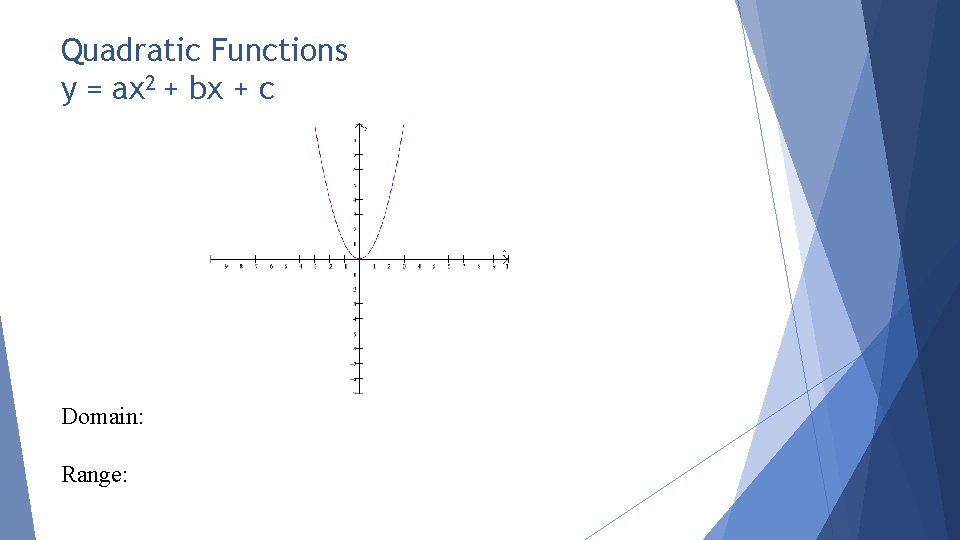
Quadratic Functions y = ax 2 + bx + c Domain: Range:

Cubic Functions Domain: Range:

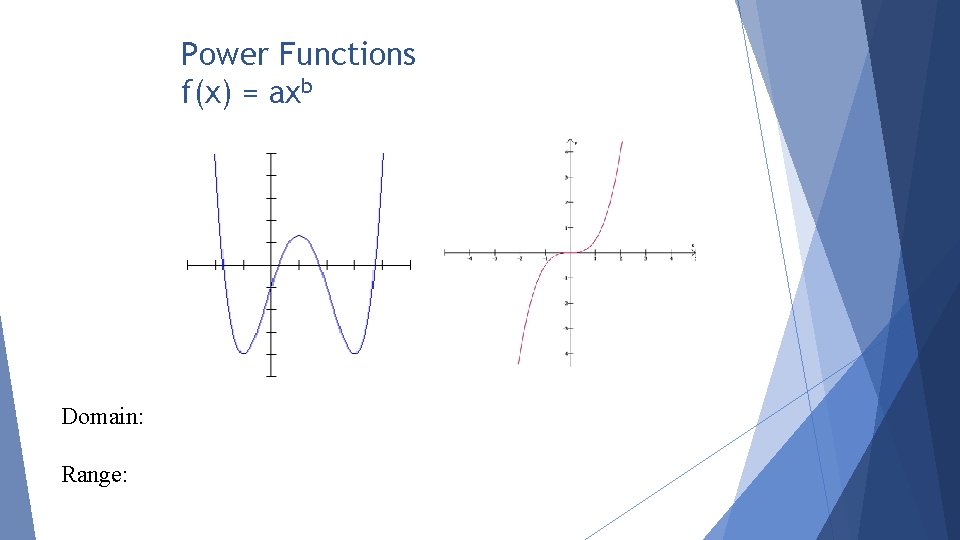
Power Functions f(x) = axb Domain: Range:

Absolute Value Functions y = │x│+1 Domain: Range:

Step Functions and Greatest Integer Function y = [x] Domain: Range:

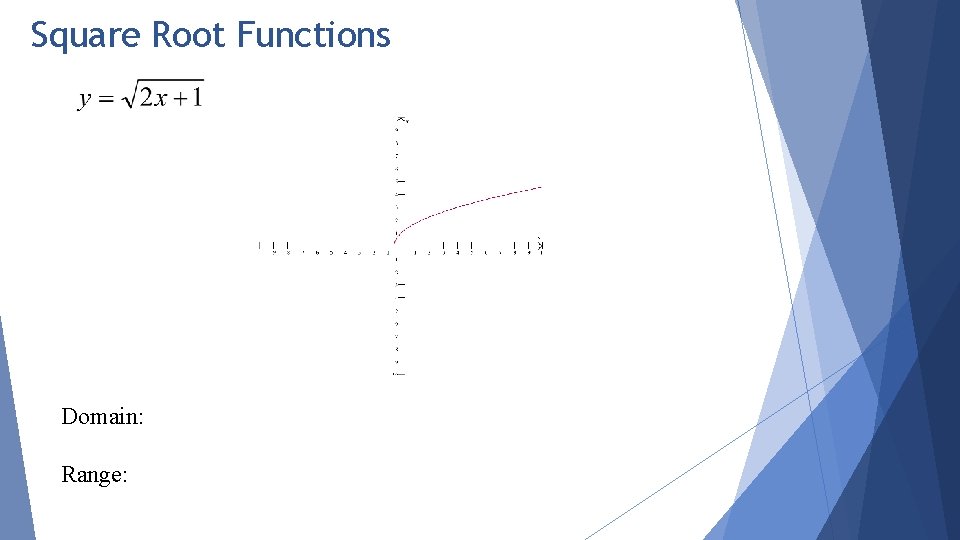
Square Root Functions Domain: Range:

Exponential Functions y = abx y = 3(2)x Domain: Range:

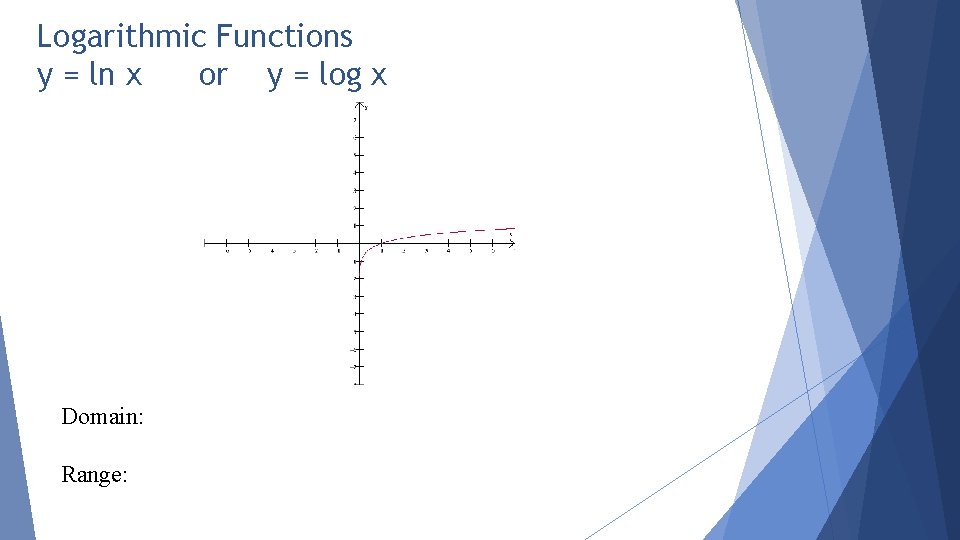
Logarithmic Functions y = ln x or y = log x Domain: Range:

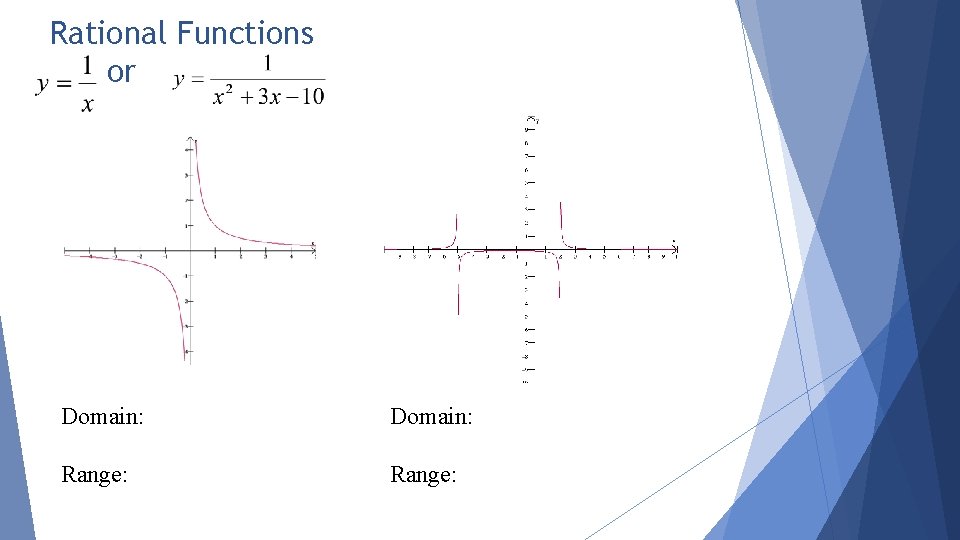
Rational Functions or Domain: Range:

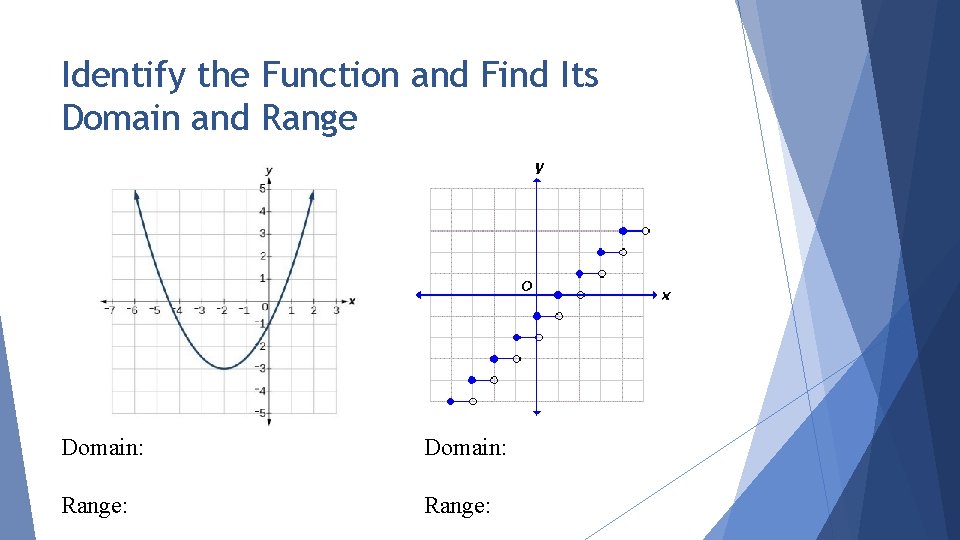
Identify the Function and Find Its Domain and Range Domain: Range:

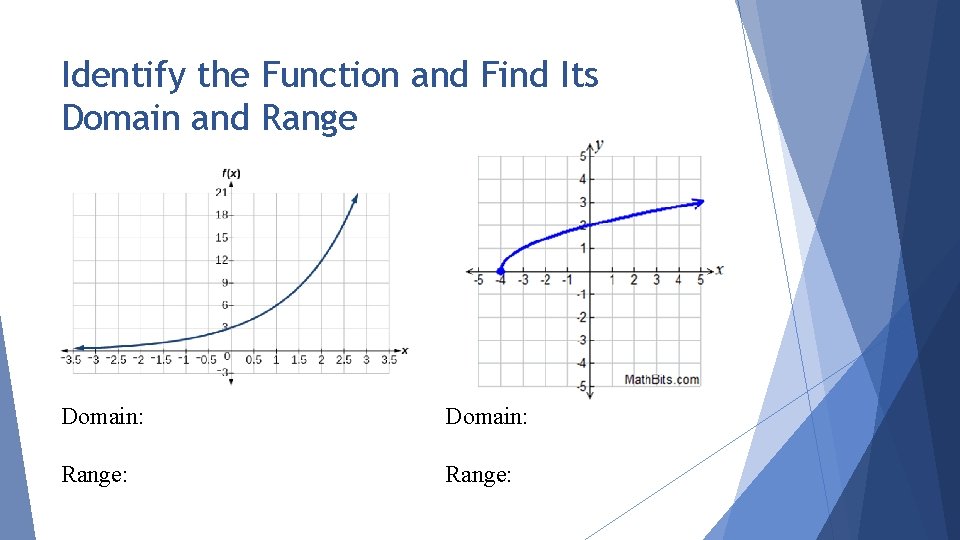
Identify the Function and Find Its Domain and Range Domain: Range:

Trig Functions

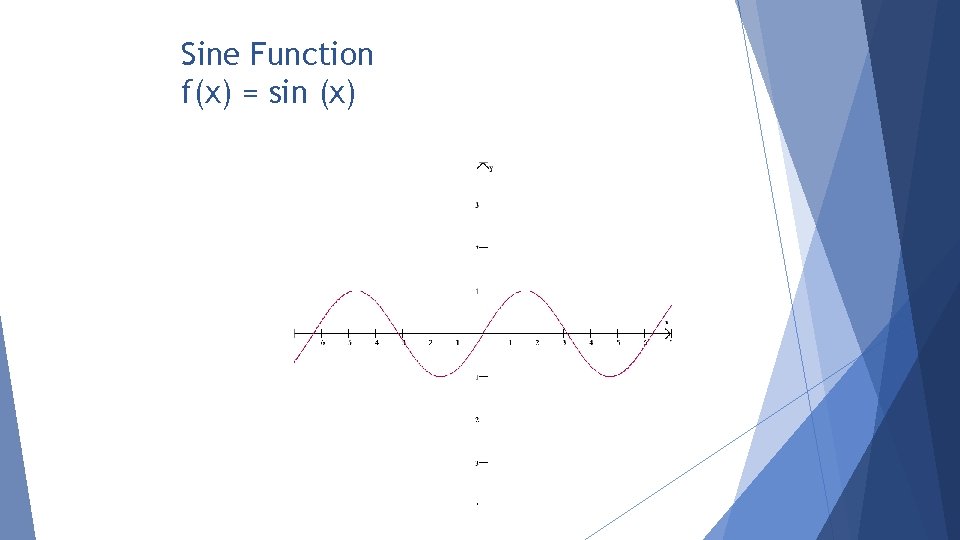
Sine Function f(x) = sin (x)

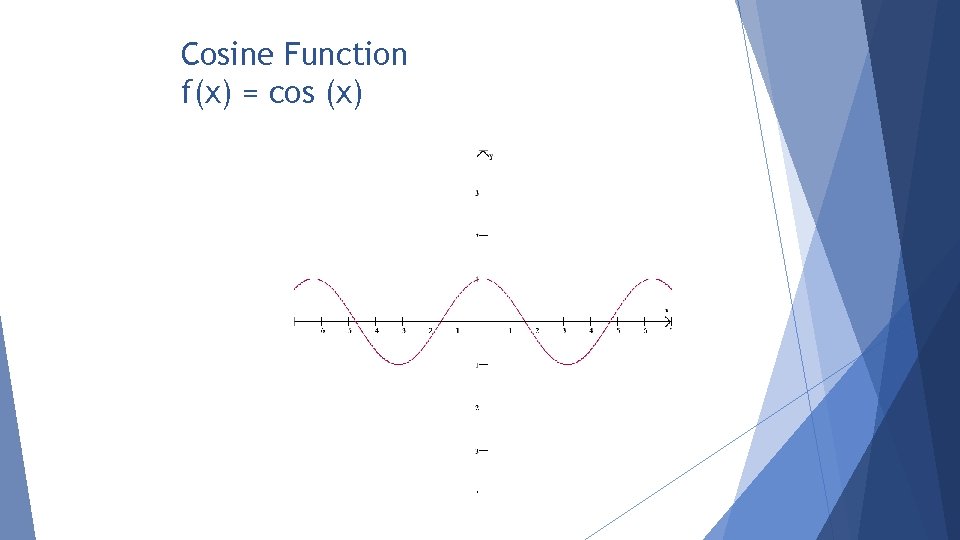
Cosine Function f(x) = cos (x)

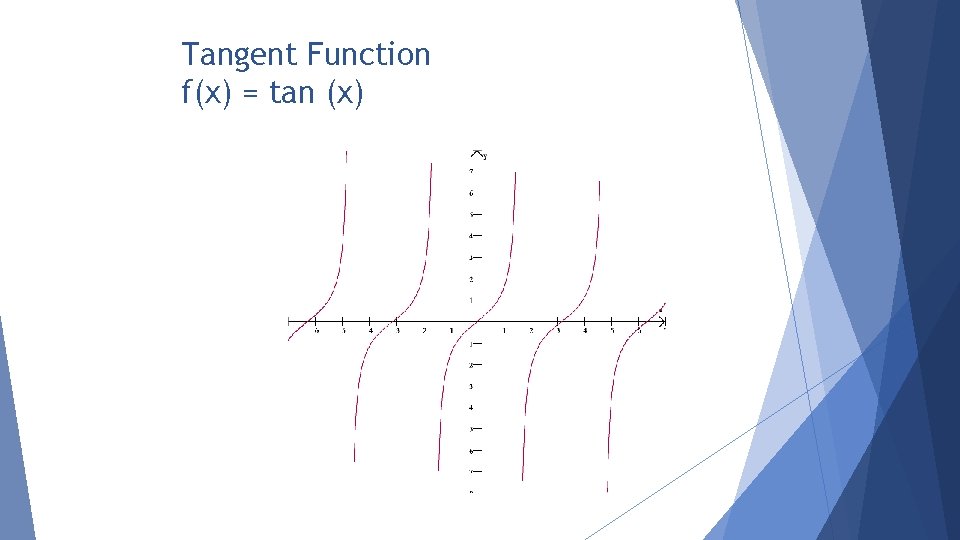
Tangent Function f(x) = tan (x)

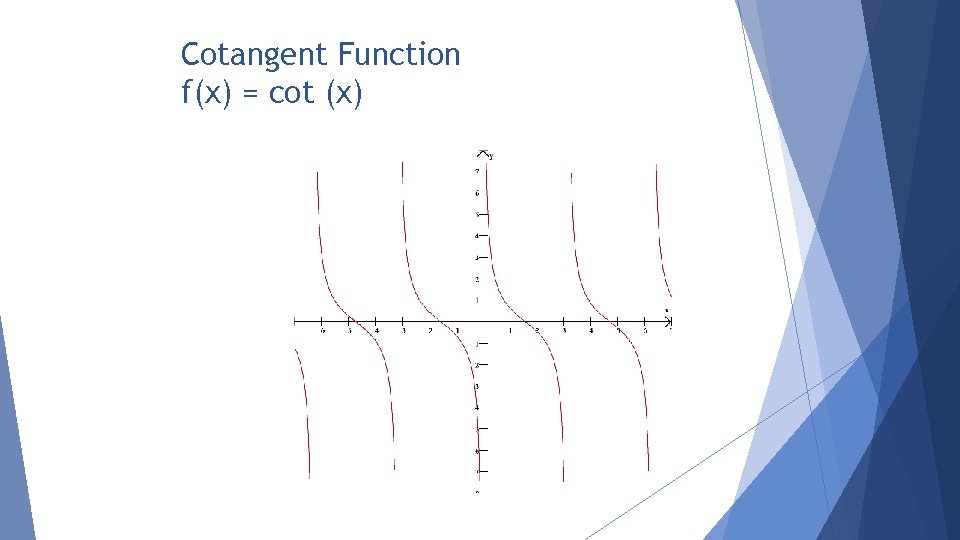
Cotangent Function f(x) = cot (x)

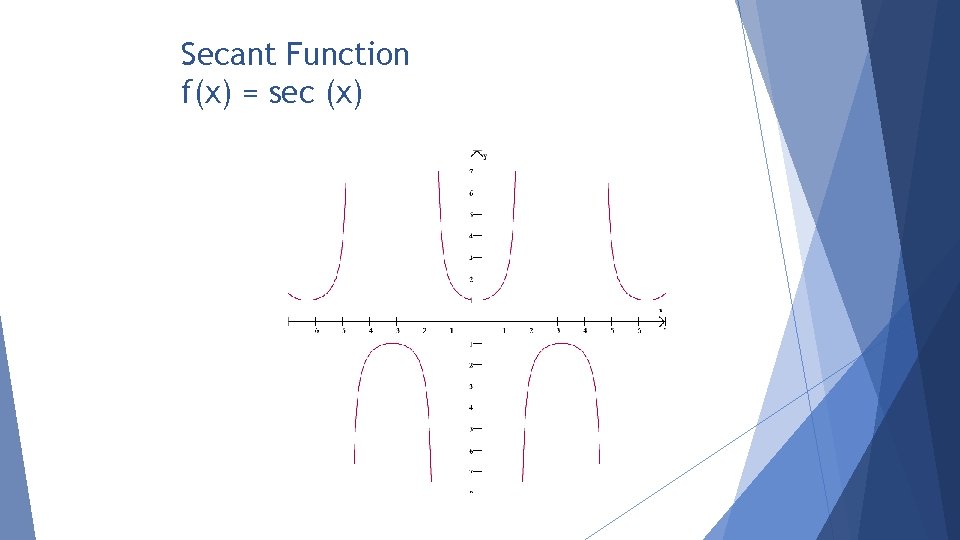
Secant Function f(x) = sec (x)

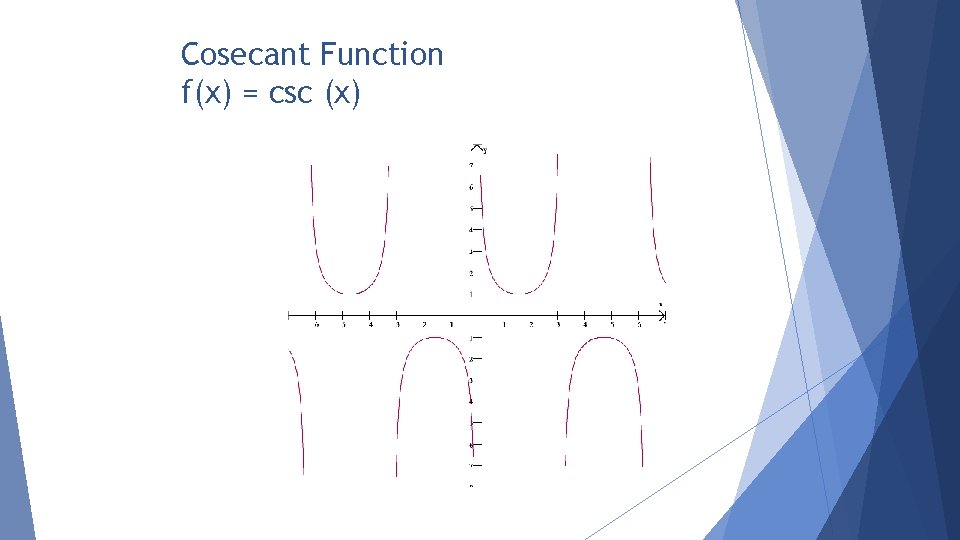
Cosecant Function f(x) = csc (x)

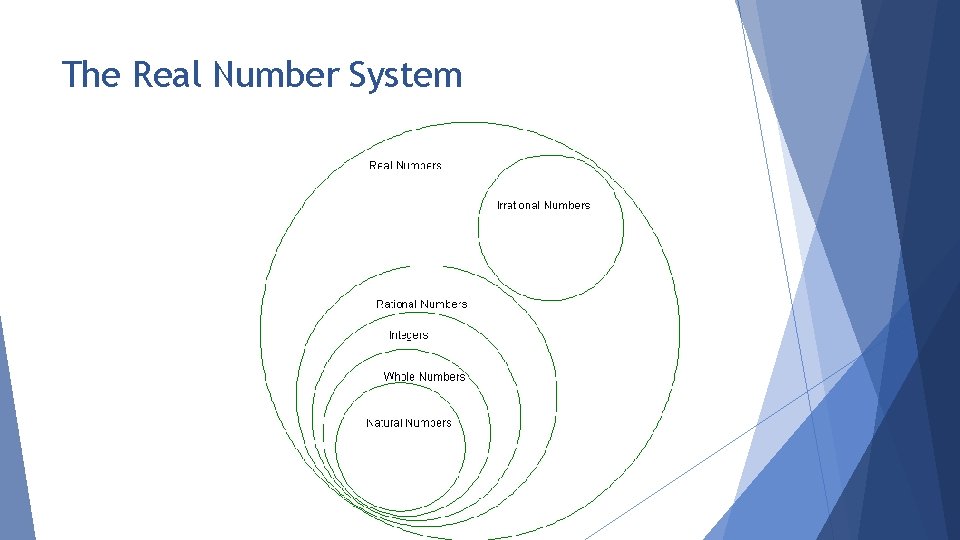
What do you know about the number system?

The Real Number System

Name the sets of numbers to which belongs. The bar over the 9 indicates that those digits repeat forever. Answer: rationals (Q) and reals (R)

Name the sets of numbers to which belongs. lies between 2 and 3 so it is not a whole number. Answer: irrationals (I) and reals (R)

Name the sets of numbers to which belongs. Answer: naturals (N), wholes (W), integers (Z), rationals (Q) and reals (R)

Name the sets of numbers to which – 23. 3 belongs. Answer: rationals (Q) and reals (R)

Name the sets of numbers to which each number belongs. a. Answer: rationals (Q) and reals (R) b. Answer: rationals (Q) and reals (R) c. Answer: irrationals (I) and reals (R) d. Answer: naturals (N), wholes (W), integers (Z) rationals (Q) and reals (R) e. 32. 1 Answer: rationals (Q) and reals (R)

Name the sets of numbers to which Answer: rationals (Q) and reals (R) belongs.

Properties of Real Numbers

Name the property illustrated by . The Additive Inverse Property says that a number plus its opposite is 0. Answer: Additive Inverse Property

Name the property illustrated by . The Distributive Property says that you multiply each term within the parentheses by the first number. Answer: Distributive Property

Name the property illustrated by each equation. a. Answer: Identity Property of Addition b. Answer: Inverse Property of Multiplication

Identify the additive inverse and multiplicative inverse for – 7. Since – 7 + 7 = 0, the additive inverse is 7. Since the multiplicative inverse is Answer: The additive inverse is 7, and the multiplicative inverse is

Identify the additive inverse and multiplicative inverse for Since . the additive inverse is the multiplicative inverse is Answer: The additive inverse is 3. and the multiplicative

Identify the additive inverse and multiplicative inverse for each number. a. 5 Answer: additive: – 5; multiplicative: b. Answer: additive: multiplicative:

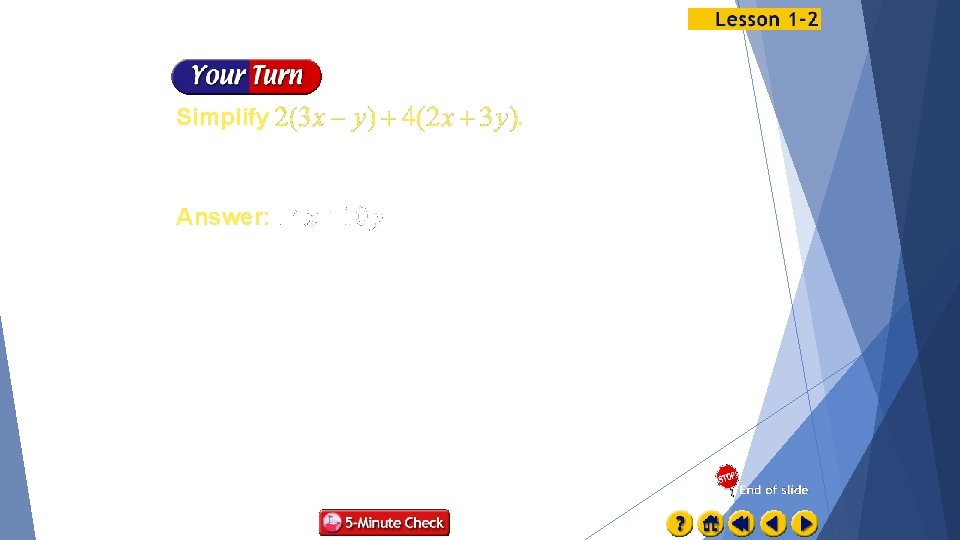
Simplify Distributive Property Multiply. Commutative Property (+) Distributive Property Answer: Simplify.

Simplify Answer: .