851 0585 04 L Modelling and Simulating Social

851 -0585 -04 L – Modelling and Simulating Social Systems with MATLAB Lesson 3 – Dynamical Systems Anders Johansson and Wenjian Yu © ETH Zürich | 2010 -03 -08

Projects § Implementation of a model from the Social -Science literature in MATLAB. § Carried out in pairs. § The projects will be assigned next week: March 15, 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 2

Lesson 3 - Contents § Differential Equations § Dynamical Systems Pendulum § Lorenz attractor § Lotka-Volterra equations § Epidemics: Kermack-Mc. Kendrick model § § Exercises 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 3

Differential equations § Solving differential equations numerically can be done by a number of schemes. The easiest way is by the 1 st order Euler’s Method: x x(t) x(t-Δt) t Δt 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 4

Dynamical systems § A dynamical system is a mathematical description of the time dependence of a point in a space. § A dynamical system is described by a set of linear/non-linear differential equations. § Even though an analytical treatment of dynamical systems is often complicated, obtaining a numerical solution is straight forward. 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 5

Pendulum § A pendulum is a simple dynamical system: L = length of pendulum (m) ϴ = angle of pendulum g = acceleration due to gravity (m/s 2) The motion is described by: 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 6

Pendulum: MATLAB code 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 7

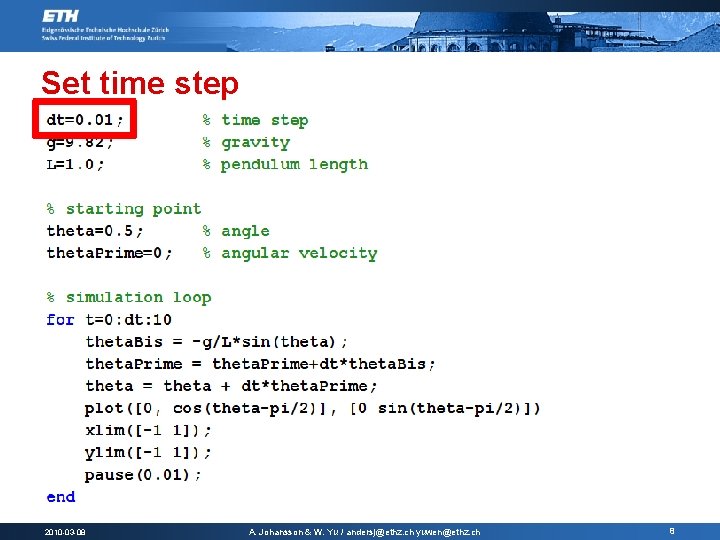
Set time step 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 8

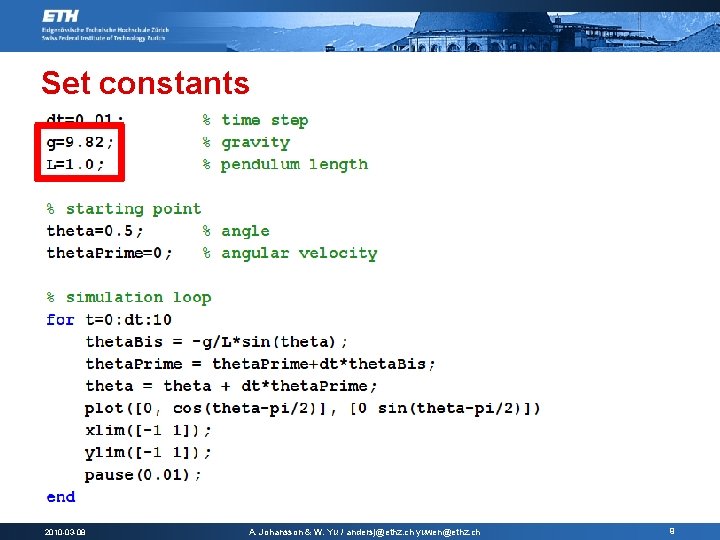
Set constants 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 9

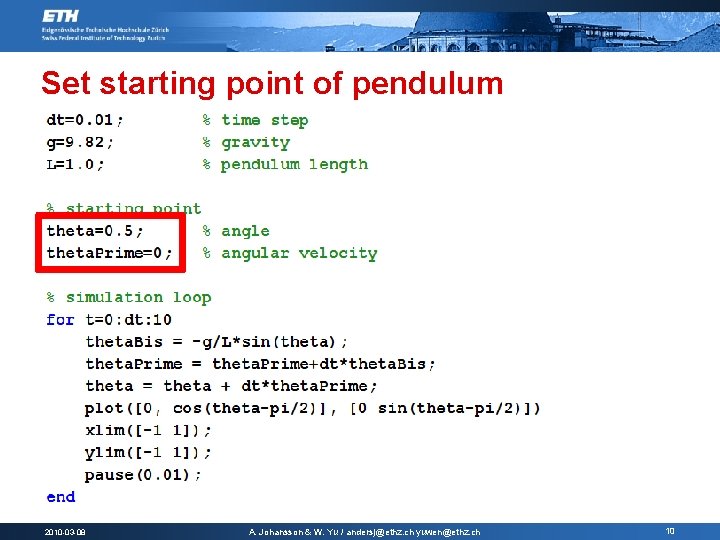
Set starting point of pendulum 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 10

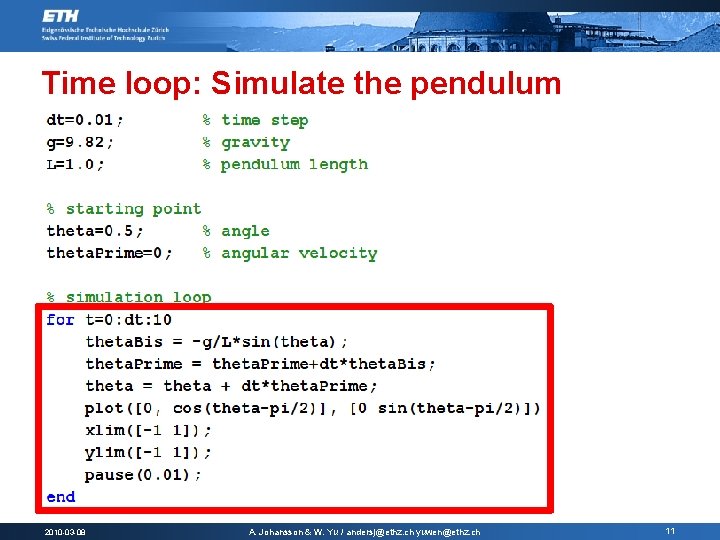
Time loop: Simulate the pendulum 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 11

Perform 1 st order Euler’s method 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 12

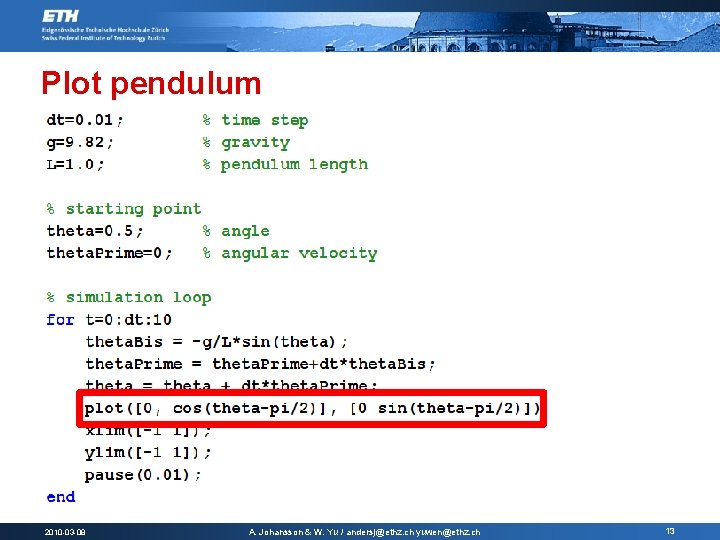
Plot pendulum 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 13

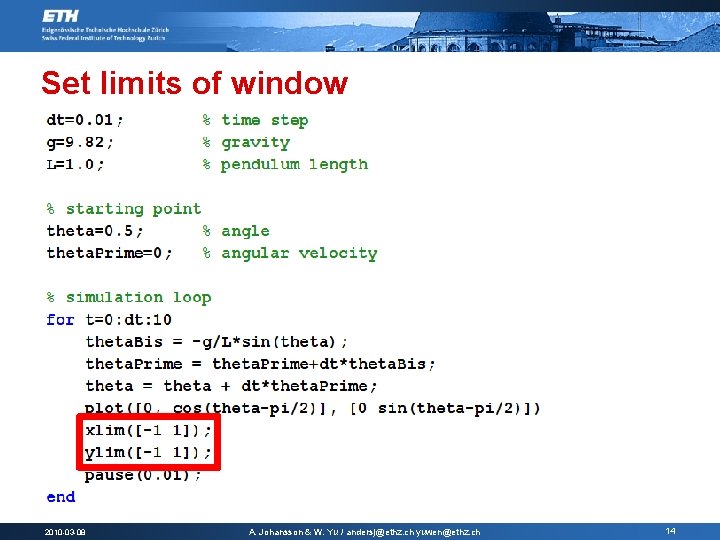
Set limits of window 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 14

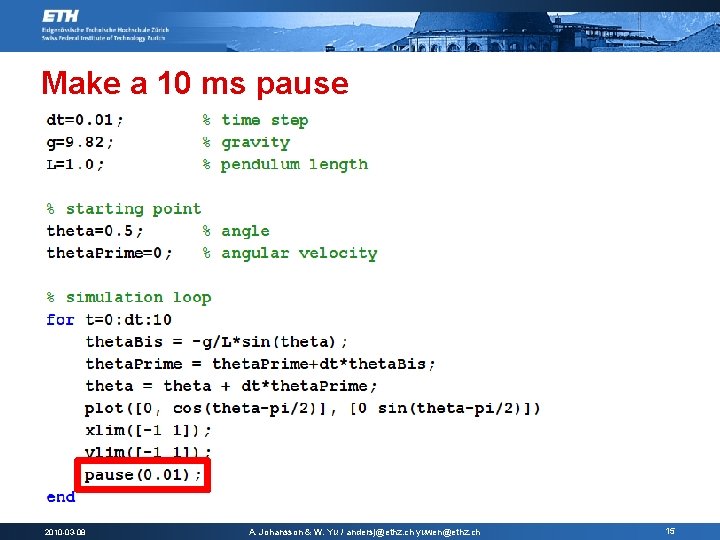
Make a 10 ms pause 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 15

Pendulum: Executing MATLAB code 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 16

Lorenz attractor § The Lorenz attractor defines a 3 -dimensional trajectory by the differential equations: § σ, r, b are parameters. 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 17

Lorenz attractor: MATLAB code 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 18

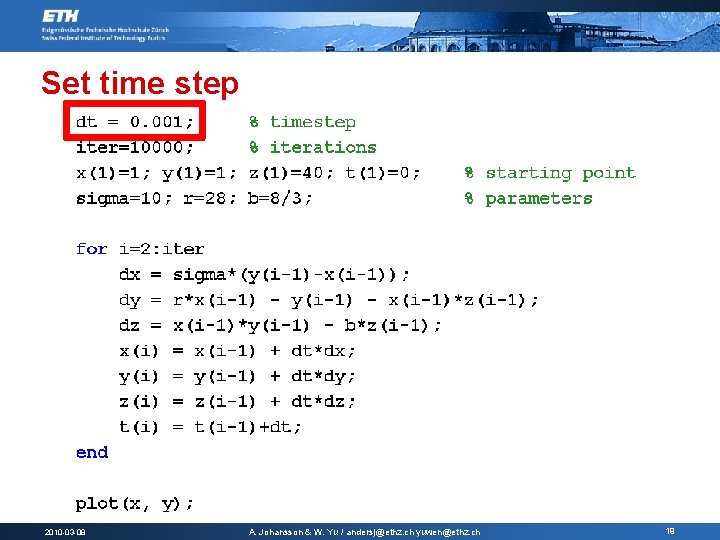
Set time step 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 19

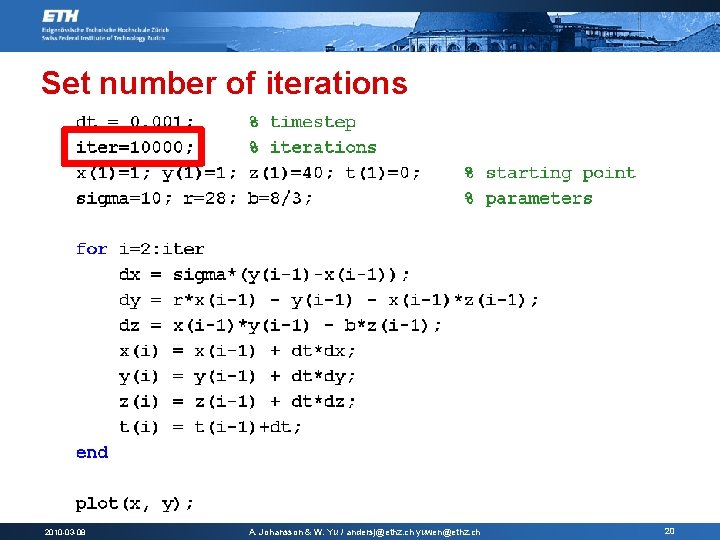
Set number of iterations 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 20

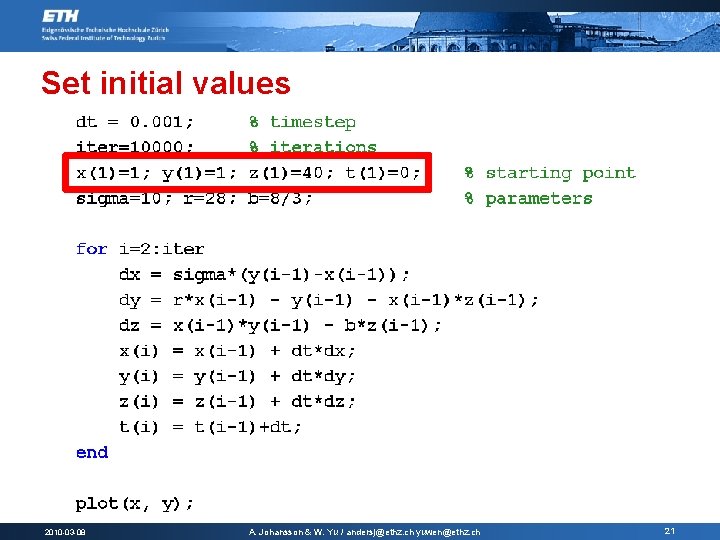
Set initial values 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 21

Set parameters 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 22

Solve the Lorenz-attractor equations 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 23

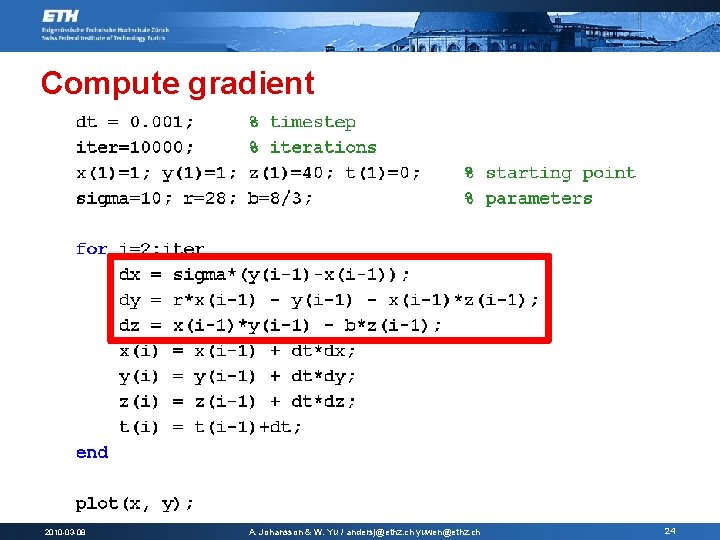
Compute gradient 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 24

Perform 1 st order Euler’s method 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 25

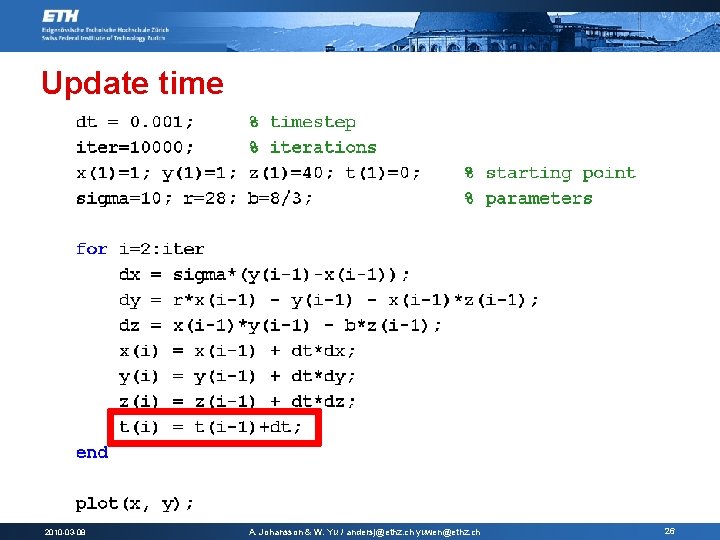
Update time 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 26

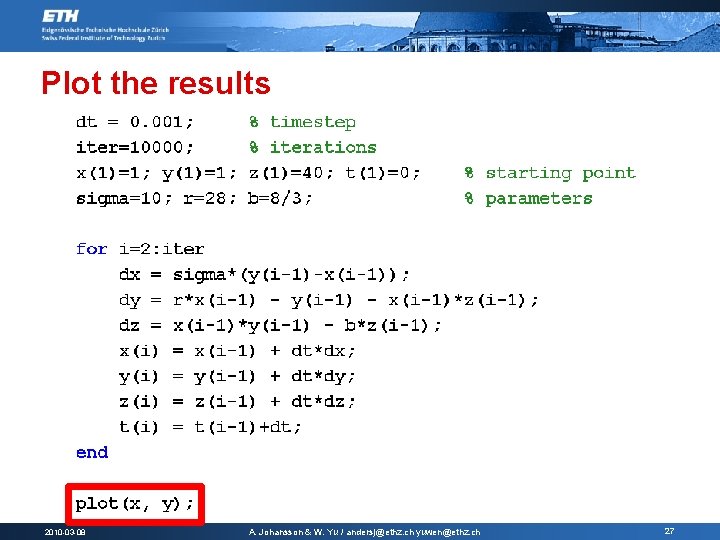
Plot the results 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 27

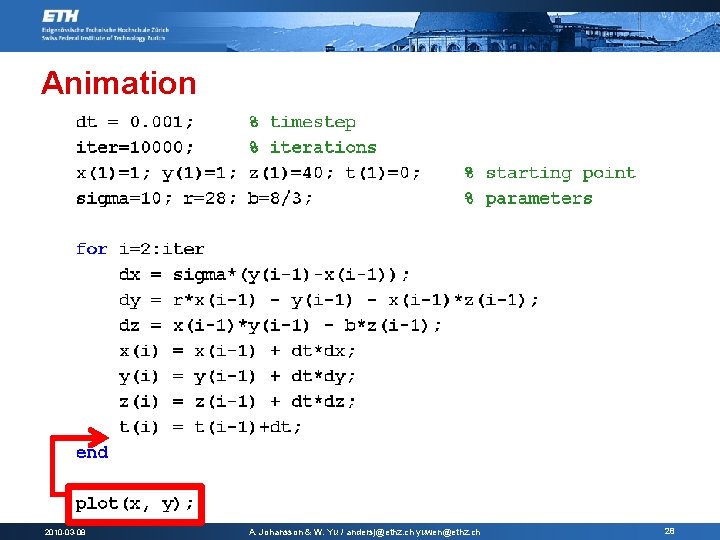
Animation 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 28

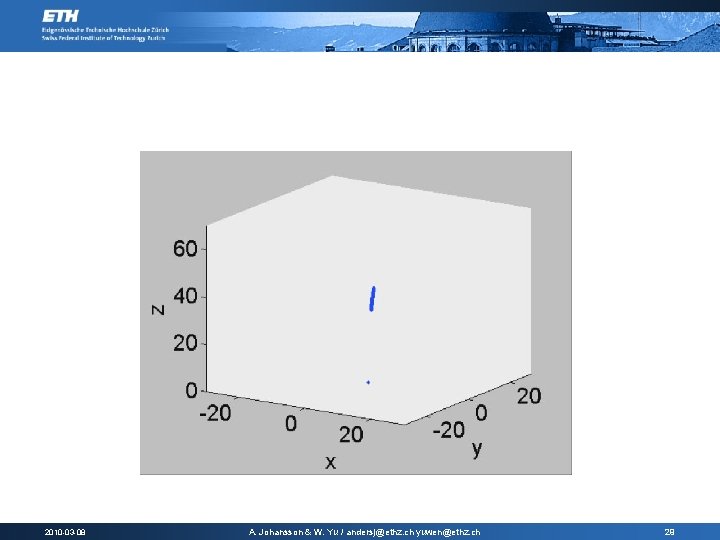
2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 29

Food chain 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 30

Lotka-Volterra equations § The Lotka-Volterra equations describe the interaction between two species, prey vs. predators, e. g. rabbits vs. foxes. x: number of prey y: number of predators α, β, γ, δ: parameters 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 31

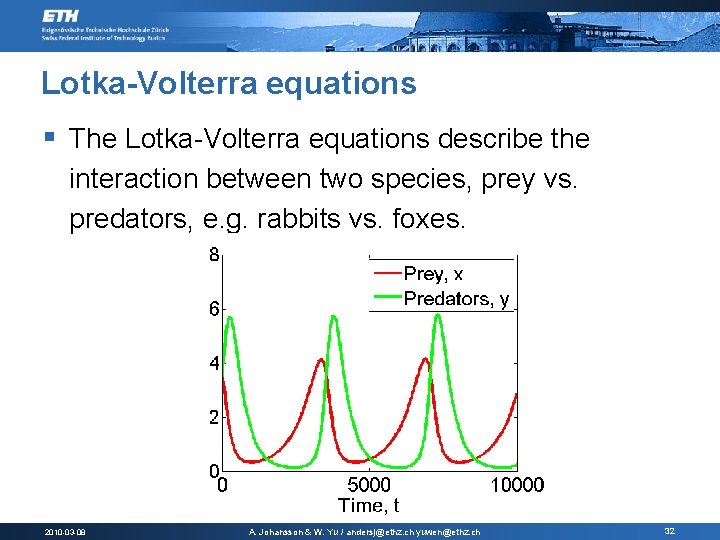
Lotka-Volterra equations § The Lotka-Volterra equations describe the interaction between two species, prey vs. predators, e. g. rabbits vs. foxes. 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 32

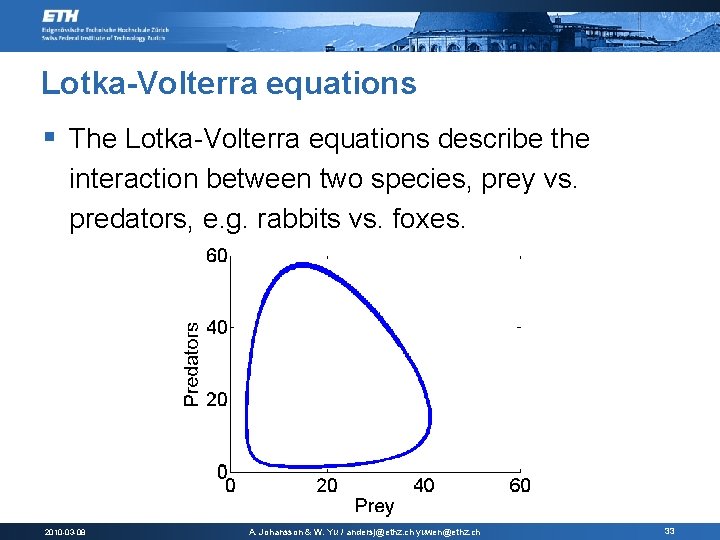
Lotka-Volterra equations § The Lotka-Volterra equations describe the interaction between two species, prey vs. predators, e. g. rabbits vs. foxes. 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 33

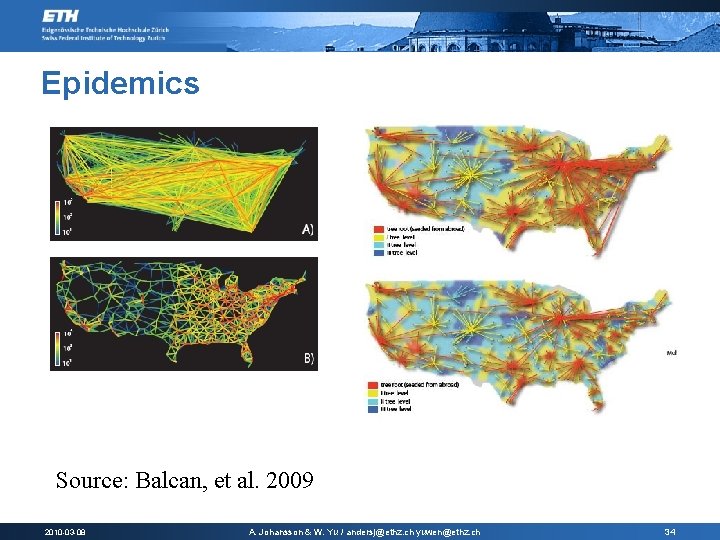
Epidemics Source: Balcan, et al. 2009 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 34

SIR model § A model for epidemics is the SIR model, which describes the interaction between Susceptible, Infected and Removed (immune) persons, for a given disease. 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 35

Kermack-Mc. Kendrick model § of diseases like the plague and cholera. A popular SIR model is the Kermack-Mc. Kendrick model. The model was proposed for explaining the spreading § The model assumes: A constant population size. § A zero incubation period. § The duration of infectivity is as long as the duration of the clinical disease. § 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 36

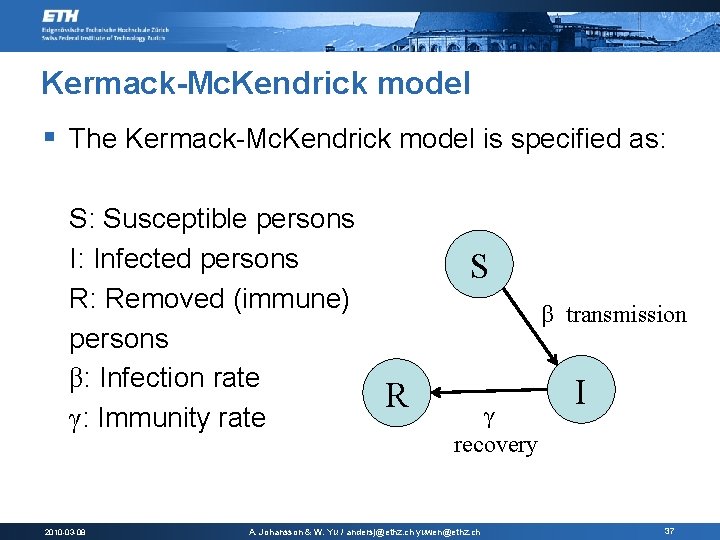
Kermack-Mc. Kendrick model § The Kermack-Mc. Kendrick model is specified as: S: Susceptible persons I: Infected persons R: Removed (immune) persons β: Infection rate γ: Immunity rate 2010 -03 -08 S β transmission R γ recovery A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch I 37

Kermack-Mc. Kendrick model § The Kermack-Mc. Kendrick model is specified as: S: Susceptible persons I: Infected persons R: Removed (immune) persons β: Infection rate γ: Immunity rate 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 38

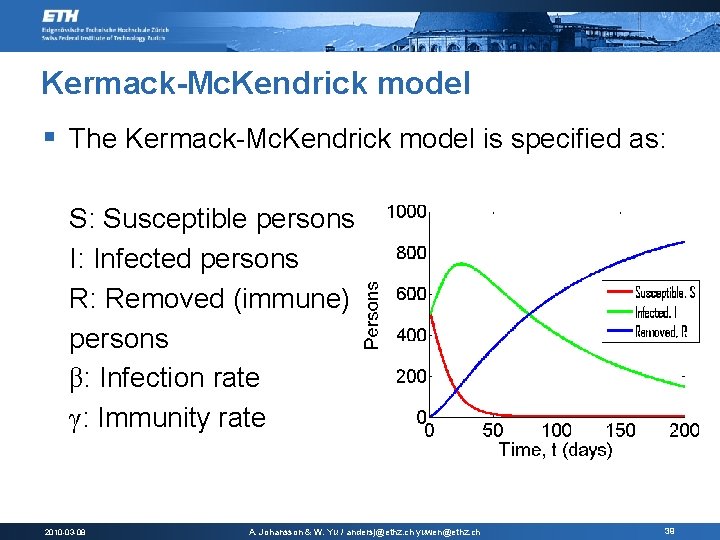
Kermack-Mc. Kendrick model § The Kermack-Mc. Kendrick model is specified as: S: Susceptible persons I: Infected persons R: Removed (immune) persons β: Infection rate γ: Immunity rate 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 39

Exercise 1 § Implement and simulate the Kermack. Mc. Kendrick model in MATLAB. Use the starting values: S=I=500, R=0, β=0. 0001, γ =0. 01 § Slides/exercises: www. soms. ethz. ch/matlab (Download only possible with Firefox!) 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 40

Exercise 2 § A key parameter for the Kermack-Mc. Kendrick model is the epidemiological threshold, βS/γ. Plot the time evolution of the model and investigate the influence of the epidemiological threshold, in particular the cases: 1. 2. βS/γ < 1 βS/γ > 1 Starting values: S=I=500, R=0, β=0. 0001 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 41

Exercise 3 - optional § Implement the Lotka-Volterra model and investigate the influence of the timestep, dt. § How small must the timestep be in order for the 1 st order Eulter‘s method to give reasonable accuracy? § Check in the MATLAB help how the functions ode 23, ode 45 etc, can be used for solving differential equations. 2010 -03 -08 A. Johansson & W. Yu / andersj@ethz. ch yuwen@ethz. ch 42