851 0585 04 L Modeling and Simulating Social

Schedule of the course Introduction to MATLAB 24. 09. 01. 10. 08. 10. 15.

Schedule of the course Introduction to MATLAB 01. 10. Different ways of Representing space

Goals of Lecture 8: students will 1. Consolidate knowledge acquired during lecture 7, through

Repetition - Generators § Generating random, realistic graphs? 1. Probabilistic generators Erdos-Renyi: start with

Repetition § We also saw a demonstration with Gephi and some efficient network generating

All began with the Drunkard’s Walk § The drunkard takes a series of steps

Stochastic Process § A stochastic process: (Xt)t ∈ I is a family of random

Stochastic Process § In reality, we observe just a single realization of such process,

White Noise (WN) § White Noise is a stochastic process whose t-th element has

Random Walk (RW) § Random Walk is a stochastic process whose tth element is

Random Walk (RW) function rw = rw(steps, drift) rw = zeros(steps, 1); for i=2:

RW: on the random increments ϵt § RW 1. ϵt = IID (0, σ2

Random Walk and Diffusion Equation § Consider a general, uncorrelated random walk where at

From Random Walk to Diffusion Equation § For the particle to go from the

The Micro-Macro Link § Using Taylor expansion, we have The following is the diffusion

The Micro-Macro Link: Take Home Msg § Diffusion: Differential Term for Diffusion Constant D

The Taylor Series § The Taylor series is an approximation of a function as

The Taylor Series in Matlab § What’s the Taylor Series for f(x) = ex

The Taylor Series in Matlab § Play with taylortool to get familiar Taylor Series

The Continuity Assumption Resources: Google 2012 -11 -12 K. Donnay & S. Balietti /

From discrete to continuous space § Cellular automaton (CA) § Continuous simulation 2012 -11

Modelling motion in continuous space § Agents are characterized by: § position - X

Modelling motion in continuous space § Next position after 1 second is given by:

Modelling motion in continuous space § Time step dt is often Time t+dt dt>1

Modelling motion in continuous space § The velocity is also y updated in time.

Modelling motion in continuous space § The velocity changes as a result of inter-individual

Modelling motion in continuous space § The changes of the velocity vector is defined

Modelling motion in continuous space § The velocity changes as a result of interactions

Modelling motion in continuous space § The velocity changes as a result of a

Modelling motion in continuous space § How to define a random move? § Choose

Modelling motion in continuous space § How to define a BIASED random move? §

Programming a Continuous Simulator § Initialization: Four elements are required to define the state

Brownian Motion %Brownian Motion t = 100; n = 1000; dt=t/n; x = zeros(1,

Pedestrian Simulation § CA model § Many-particle model 2012 -11 -12 K. Donnay &

CA Model (A. Kirchner, A. Schadschneider, Phys. A, 2002) 2012 -11 -12 K. Donnay

Many-particle Model (Helbing, Nature, 2000) Social Force Model § Desired velocity § Repulsive force

Grids Vs Continuum Space § Easier § (more) Complex § Implementation dependant § Elegant

Examples from Previous Semesters § Train Boarding Simulation (Graf & Krebs, Fall 2010) 2012

Examples from Previous Semesters § Love Parade Disaster (Guthrie & Fougner, Fall 2010) 2012

Examples from Previous Semesters § Airplane Evacuation (Bühler & Heer, Spring 2011) 2012 -11

Examples from Previous Semesters § Flooding Evacuation (Crameri & Thielmann, Fall 2011) 2012 -11

Examples from Previous Semesters § Desert Ant Navigation (Megaro & Rudel, Fall 2011) 2012

Projects § Today, there are no exercises. § You can work on your projects

References § http: //en. wikipedia. org/wiki/Taylor_expansion § http: //en. wikipedia. org/wiki/Random_walk § Toolbox for

Git. Hub Links § Train Boarding Simulation (Graf & Krebs, Fall 2010) https: //github.

Slides: 49

Download presentation

851 -0585 -04 L – Modeling and Simulating Social Systems with MATLAB Lecture 8 – Continuous Simulations Karsten Donnay and Stefano Balietti Chair of Sociology, in particular of Modeling and Simulation © ETH Zürich | 2012 -11 -12

Schedule of the course Introduction to MATLAB 24. 09. 01. 10. 08. 10. 15. 10. 22. 10. 29. 10. Working on projects (seminar thesis) 05. 11. 12. 11. 19. 11. Introduction to social-science modeling and simulations 26. 11. 03. 12. 10. 12. 17. 12. 2012 -11 -12 Handing in seminar thesis and giving a presentation K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 2

Schedule of the course Introduction to MATLAB 01. 10. Different ways of Representing space 08. 10. Dynamical Systems (no-space) 15. 10. Cellular Automata (grid) 24. 09. 22. 10. 29. 10. Working on projects (seminar thesis) 05. 11. 12. 11. Networks (graphs) Continuous Space (…) 19. 11. 26. 11. 03. 12. 10. 12. 17. 12. 2012 -11 -12 Handing in seminar thesis and giving a presentation K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 3

Goals of Lecture 8: students will 1. Consolidate knowledge acquired during lecture 7, through brief repetition of the main points. 2. Receive an essential, but commensurate introduction about Stochastic Processes. 3. Discover the Micro-Macro link in continuous modeling, bridging Random Walk and Diffusion Equation. 4. Understand the basics of Motion Dynamics and learn how to simulate processes like Brownian Motion in continuous space. 5. Have a closer glance into two examples of Pedestrian Simulation, confronting grids with continuous space. 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 4

Repetition - Generators § Generating random, realistic graphs? 1. Probabilistic generators Erdos-Renyi: start with n nodes, connect with probability p 2. Degree-based generators Assign degrees to nodes; add edges, so that they match the original degree distribution 3. Process-based generators preferential attachment (Barabasi), attach new node: 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 5

Repetition § We also saw a demonstration with Gephi and some efficient network generating MATLAB functions § USE THEM and existing implementation from previous terms in your work (and cite them properly!) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 6

All began with the Drunkard’s Walk § The drunkard takes a series of steps away from the lamp post, each with a random angle. (Figure Resource: Sethna JP, 2006) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 7

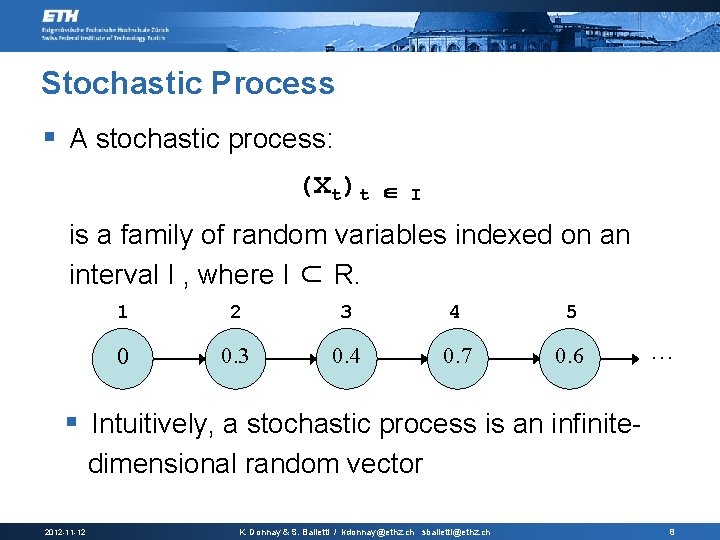
Stochastic Process § A stochastic process: (Xt)t ∈ I is a family of random variables indexed on an interval I , where I ⊂ R. 1 2 3 4 5 0 0. 3 0. 4 0. 7 0. 6 … § Intuitively, a stochastic process is an inﬁnitedimensional random vector 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 8

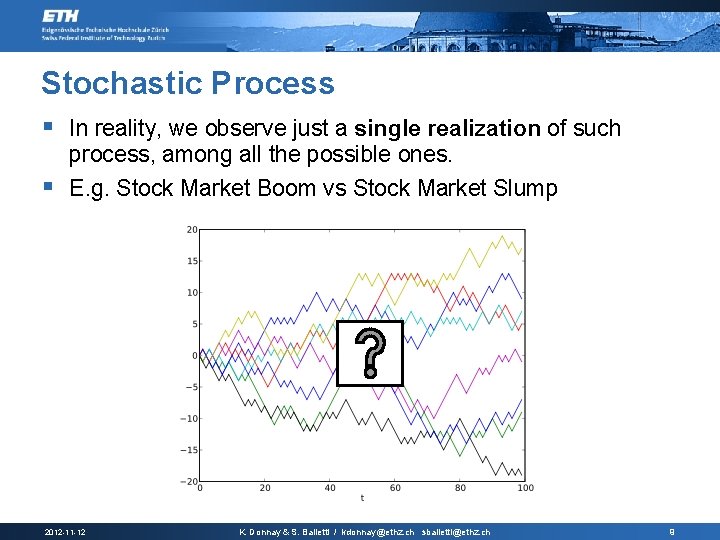
Stochastic Process § In reality, we observe just a single realization of such process, among all the possible ones. § E. g. Stock Market Boom vs Stock Market Slump 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 9

White Noise (WN) § White Noise is a stochastic process whose t-th element has the following properties: E(xt) = 0 § E(xt 2) = σ2 § γk= 0 for |k| > 0 (autocorrelation coeff) § § That means that the white noise is succession of uncorrelated random variables with zero mean and constant variance. 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 10

Random Walk (RW) § Random Walk is a stochastic process whose tth element is determined as follows: Xt = µ + Xt − 1 + ϵt § µ is the drift, constantly leading the process towards its sign § ϵt represents the random increments. 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 11

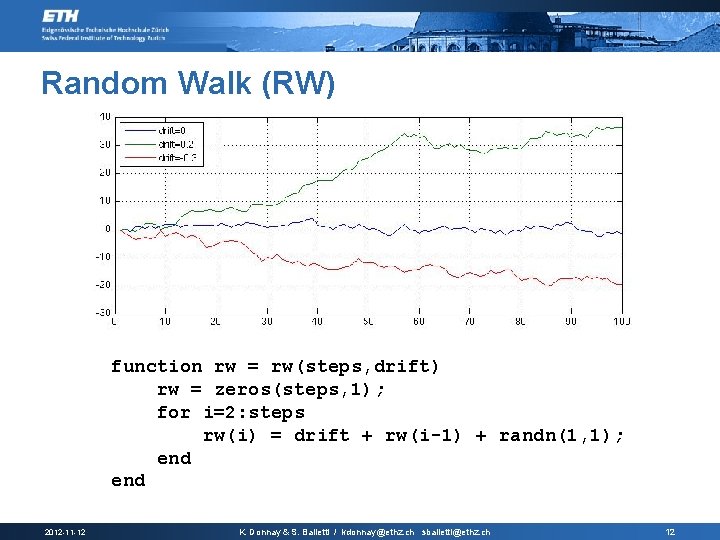
Random Walk (RW) function rw = rw(steps, drift) rw = zeros(steps, 1); for i=2: steps rw(i) = drift + rw(i-1) + randn(1, 1); end 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 12

RW: on the random increments ϵt § RW 1. ϵt = IID (0, σ2 ). Independent and Identically Distributed. § classical hypothesis -> computational simpliﬁcation § RW 2. ϵt are still independent, but no more identically distributed. § Di�erent density functions across times are possible § RW 3. ϵt are simply uncorrelated and basically White Noise. This is the weakest RW form. § Admits non linear correlations among past values. Campbell et al 1997 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 13

Random Walk and Diffusion Equation § Consider a general, uncorrelated random walk where at each time step a step the particle’s position changes by : § The probability distribution for each step is , which has zero mean and standard deviation. 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 14

From Random Walk to Diffusion Equation § For the particle to go from the step at time to at time , . Such event occurs with probability times the probability density . Therefore, we have 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 15

The Micro-Macro Link § Using Taylor expansion, we have The following is the diffusion equation 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 16

The Micro-Macro Link: Take Home Msg § Diffusion: Differential Term for Diffusion Constant D § Constant drift of the ensemble with the characteristic constant D given by the properties of RW § A simple and controllable process such as RW applied to single agents can give rise to seemingly organized macroscopic behavior of the ensemble. 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 17

The Taylor Series § The Taylor series is an approximation of a function as an infinite sum of terms calculated from the values of its derivatives at a single point. § F(x) can thus be rewritten as: § § 2012 -11 -12 § a = single point K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 18

The Taylor Series in Matlab § What’s the Taylor Series for f(x) = ex ? >> syms x >> f = exp(x); >> taylor(f) ans = x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 19

The Taylor Series in Matlab § What’s the Taylor Series for f(x) = ex ? >> syms x >> f = exp(x); >> taylor(f) ans = x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1 And this is good because we reduced the complexity of the function from exponential to polinomial! 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 20

The Taylor Series in Matlab § Play with taylortool to get familiar Taylor Series 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 21

The Continuity Assumption Resources: Google 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 22

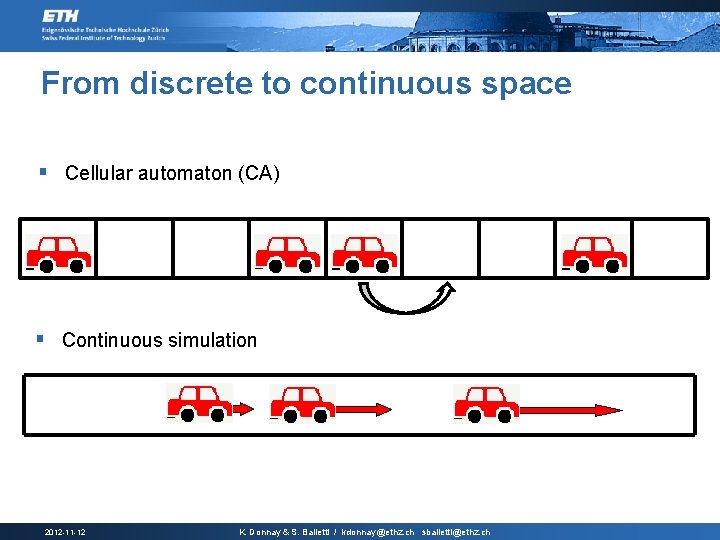
From discrete to continuous space § Cellular automaton (CA) § Continuous simulation 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Modelling motion in continuous space § Agents are characterized by: § position - X (m) - Y (m) § velocity - Vx (m/s) - Vy (m/s) Vy y x 2012 -11 -12 Vx K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

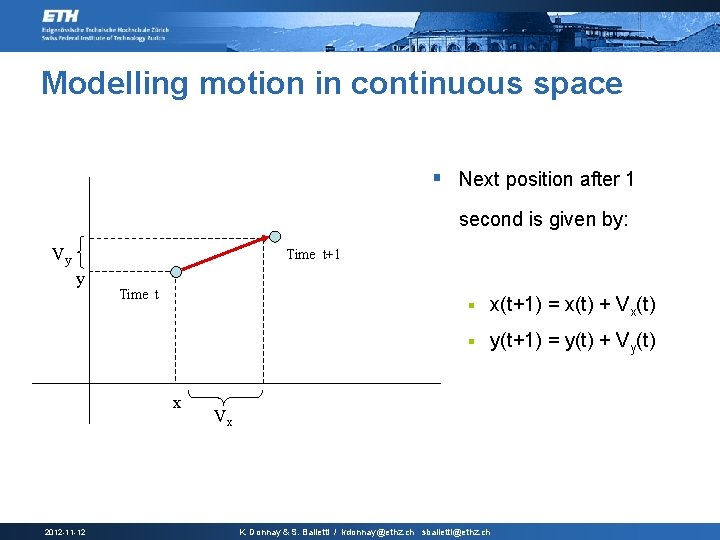
Modelling motion in continuous space § Next position after 1 second is given by: Vy Time t+1 y Time t x 2012 -11 -12 § x(t+1) = x(t) + Vx(t) § y(t+1) = y(t) + Vy(t) Vx K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Modelling motion in continuous space § Time step dt is often Time t+dt dt>1 Vy y Time t+dt dt<1 Time t x 2012 -11 -12 different from 1: § x(t+dt) = x(t) + dt Vx(t) § y(t+dt) = y(t) + dt Vy(t) Vx K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

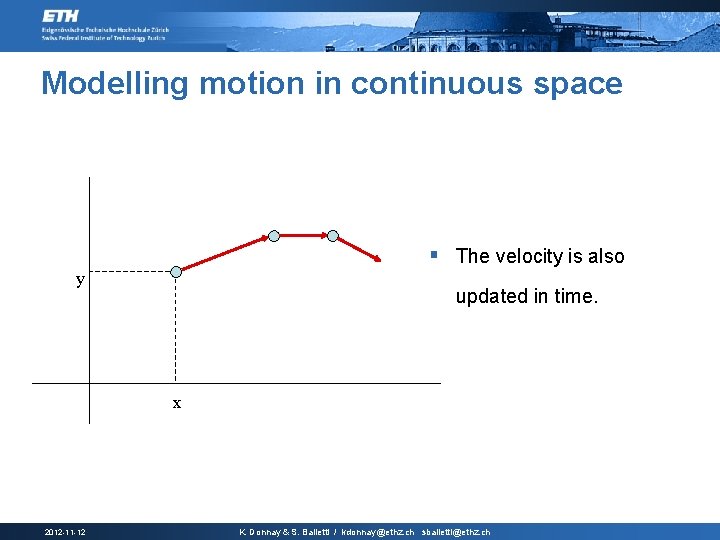
Modelling motion in continuous space § The velocity is also y updated in time. x 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

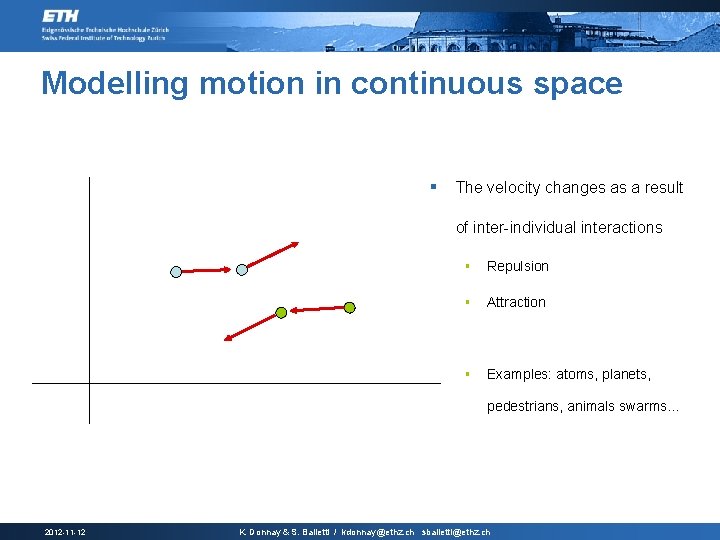
Modelling motion in continuous space § The velocity changes as a result of inter-individual interactions § Repulsion § Attraction § Examples: atoms, planets, pedestrians, animals swarms… 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Modelling motion in continuous space § The changes of the velocity vector is defined by an acceleration. 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

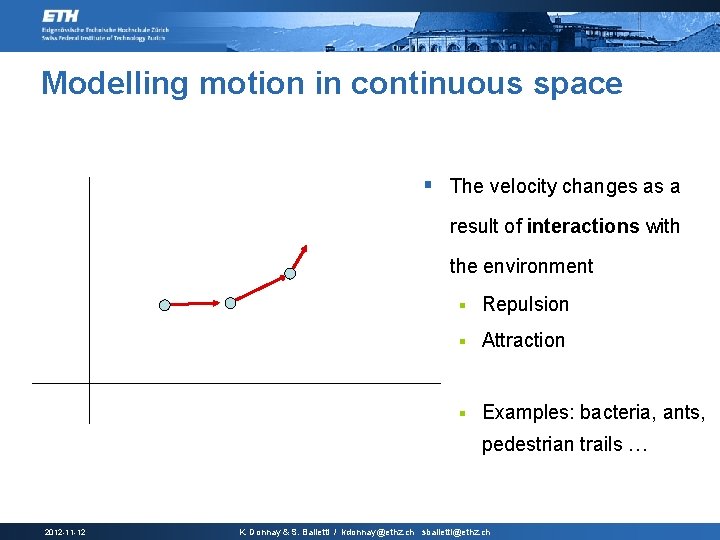
Modelling motion in continuous space § The velocity changes as a result of interactions with the environment § Repulsion § Attraction § Examples: bacteria, ants, pedestrian trails … 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Modelling motion in continuous space § The velocity changes as a result of a random process: § With or without bias § Example: exploration behaviour in many species of animals 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

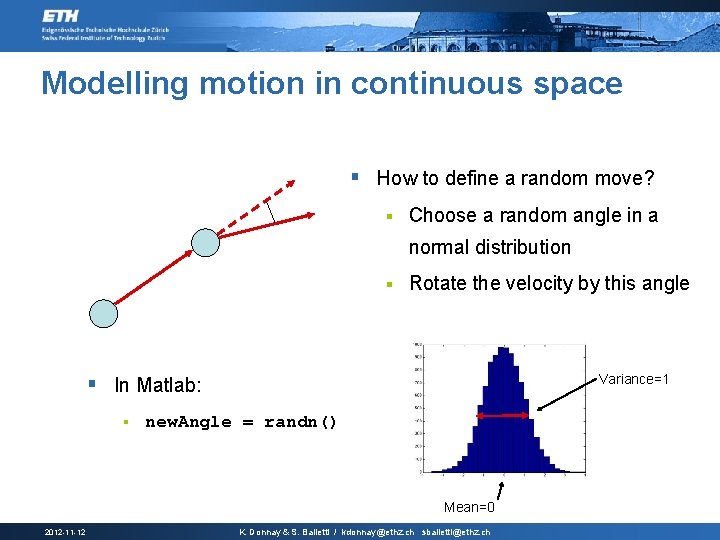
Modelling motion in continuous space § How to define a random move? § Choose a random angle in a normal distribution § Rotate the velocity by this angle Variance=1 § In Matlab: § new. Angle = randn() Mean=0 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Modelling motion in continuous space § How to define a random move? § Choose a random angle in a normal distribution § Rotate the velocity by this angle § In Matlab: 2012 -11 -12 § mean. Val=2; § v=0. 1; § new. Angle = mean. Val + v*randn() K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Modelling motion in continuous space § How to define a BIASED random move? § Unbalance the distribution toward positive or negative values § In Matlab: 2012 -11 -12 § mean. Val=2; § v=0. 1; § new. Angle = mean. Val + v*(offset + randn()) K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Programming a Continuous Simulator § Initialization: Four elements are required to define the state of individuals § The velocity is updated first, and then the position as a function of the velocity and the time step 2012 -11 -12 X Y Vx Vy = = [1 [2 [0 [1 1 1 0 1 3 ]; 1]; 0. 5]; for t=1: dt: T for p=1: N [Vx(p) Vy(p)] = update( …) ; X(p) = X(p) + dt*Vx(p) ; Y(p) = Y(p) + dt*Vy(p) ; end K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch

Brownian Motion %Brownian Motion t = 100; n = 1000; dt=t/n; x = zeros(1, n); y = zeros(1, n); dx = zeros(1, n); dy = zeros(1, n); x(1) = 0; y(1) = 0; hold on; k = 1; for j=2: n x(j)= x(j-1) +… sqrt(dt)*randn; y(j)= y(j-1) +… sqrt(dt)*randn; plot([x(j-1), x(j)], … [y(j-1), y(j)]); k = k + 1; end 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 36

Pedestrian Simulation § CA model § Many-particle model 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 37

CA Model (A. Kirchner, A. Schadschneider, Phys. A, 2002) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 38

Many-particle Model (Helbing, Nature, 2000) Social Force Model § Desired velocity § Repulsive force 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 39

Grids Vs Continuum Space § Easier § (more) Complex § Implementation dependant § Elegant § More Limited § Extremely Powerful § One Element per Cell § Agents Float in Space § Computationally more § Computationally faster intensive 2012 -11 -12 (with analytical derivates) K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 40

Grids Vs Continuum Space § Easier § (more) Complex § Implementation dependant § Elegant § More Limited § Extremely Powerful § One Element per Cell § Agents Float in Space § Computationally more § Computationally faster intensive (with analytical derivates) You can write a good paper with both approaches if you have a good idea 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 41

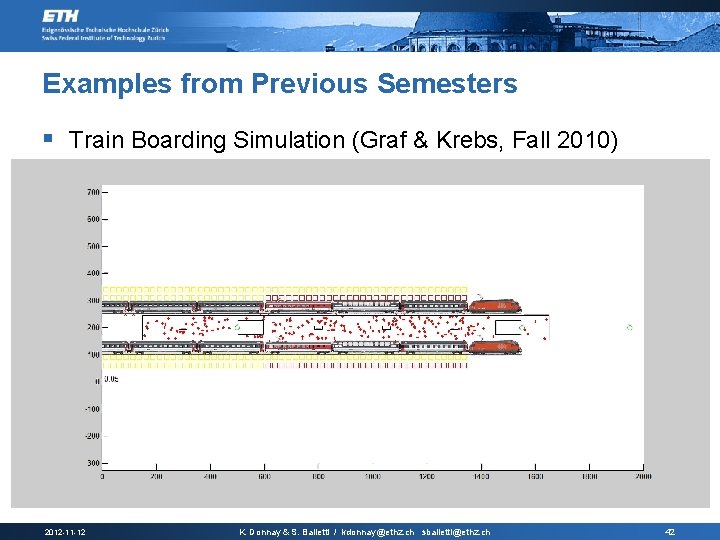
Examples from Previous Semesters § Train Boarding Simulation (Graf & Krebs, Fall 2010) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 42

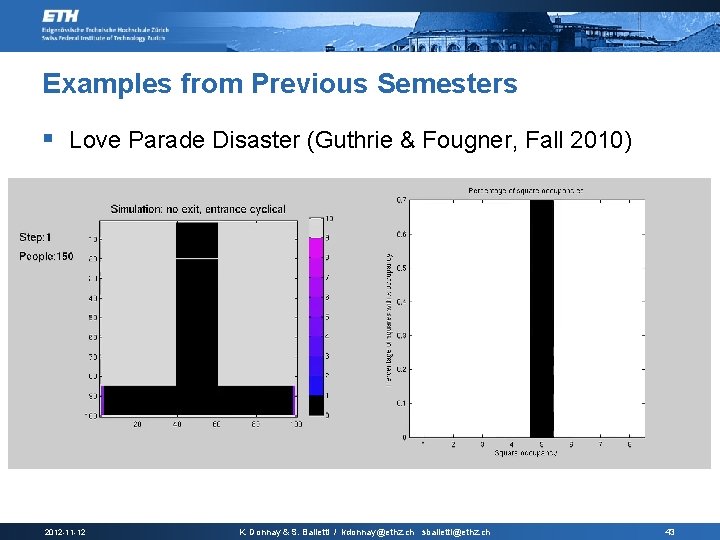
Examples from Previous Semesters § Love Parade Disaster (Guthrie & Fougner, Fall 2010) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 43

Examples from Previous Semesters § Airplane Evacuation (Bühler & Heer, Spring 2011) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 44

Examples from Previous Semesters § Flooding Evacuation (Crameri & Thielmann, Fall 2011) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 45

Examples from Previous Semesters § Desert Ant Navigation (Megaro & Rudel, Fall 2011) 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 46

Projects § Today, there are no exercises. § You can work on your projects and we will supervise you. § If you have preliminary results we are happy to discuss them with you… 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 47

References § http: //en. wikipedia. org/wiki/Taylor_expansion § http: //en. wikipedia. org/wiki/Random_walk § Toolbox for different random walks: http: //www. mathworks. com/matlabcentral/fileexchange/22003 § Nature 407, 487 -490 (2000) Simulating dynamical features of escape panic. Dirk Helbing, Illés Farkas and Tamás Vicsek § The Econometrics of Financial Markets. 1997. John Y. Campbell, Andrew W. Lo, A. Craig Mac. Kinsley. Princeton University Press. 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 48

Git. Hub Links § Train Boarding Simulation (Graf & Krebs, Fall 2010) https: //github. com/msssm/Train-Boarding § Love Parade Disaster (Guthrie & Fougner, Fall 2010) https: //github. com/msssm/Love_Parade_2010 § Airplane Evacuation (Bühler & Heer, Spring 2011) https: //github. com/msssm/Airplane_Evacuation_2011_FS § Flooding Evacuation (Crameri & Thielmann, Fall 2011) https: //github. com/mthielma/SOCIAL_MODELING § Desert Ant Navigation (Megaro & Rudel, Fall 2011) https: //github. com/erudel/desert_ant_behavior_gordonteam 2012 -11 -12 K. Donnay & S. Balietti / kdonnay@ethz. ch sbalietti@ethz. ch 49