8051 8051 1 immediate constants MOV A 127

8051 指令

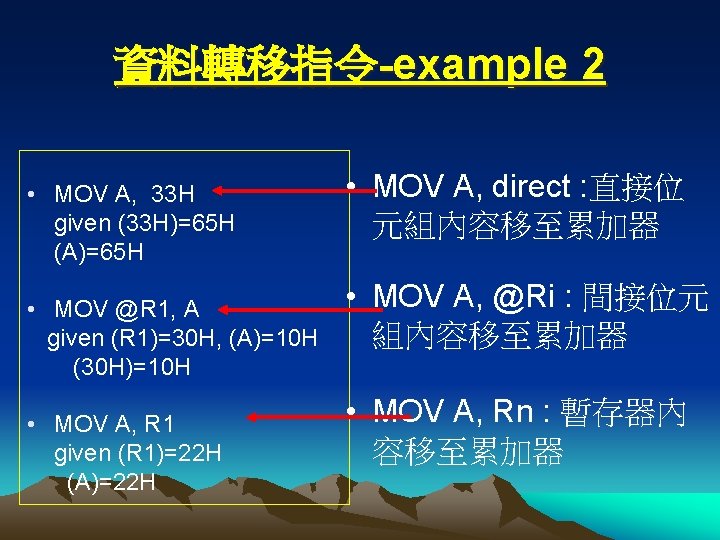
8051定址模式 1. 立即常數定址（immediate constants） MOV A, #127 (A)=127 常數 127 A 2. 直接定址（direct addressing） MOV A, 7 FH Cpu內記憶體 7 FH (A)=(7 FH)=65 H A

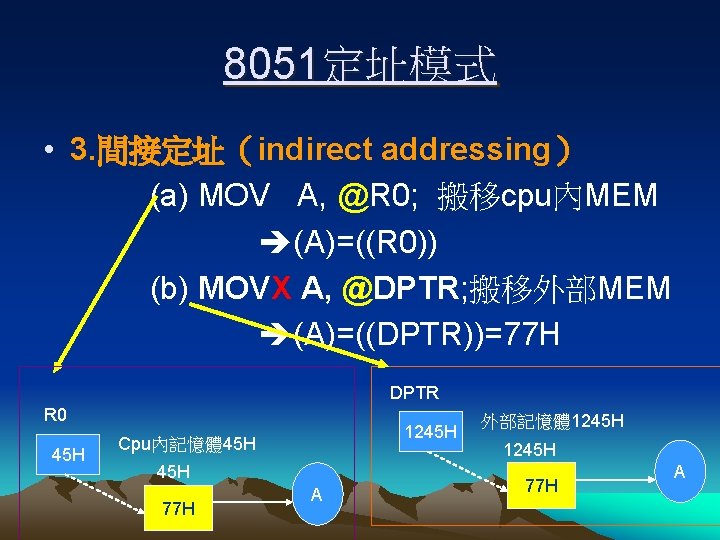
8051定址模式 • 3. 間接定址（indirect addressing） (a) MOV A, @R 0; 搬移cpu內MEM (A)=((R 0)) (b) MOVX A, @DPTR; 搬移外部MEM (A)=((DPTR))=77 H DPTR R 0 45 H 1245 H Cpu內記憶體 45 H 77 H A 外部記憶體 1245 H 77 H A

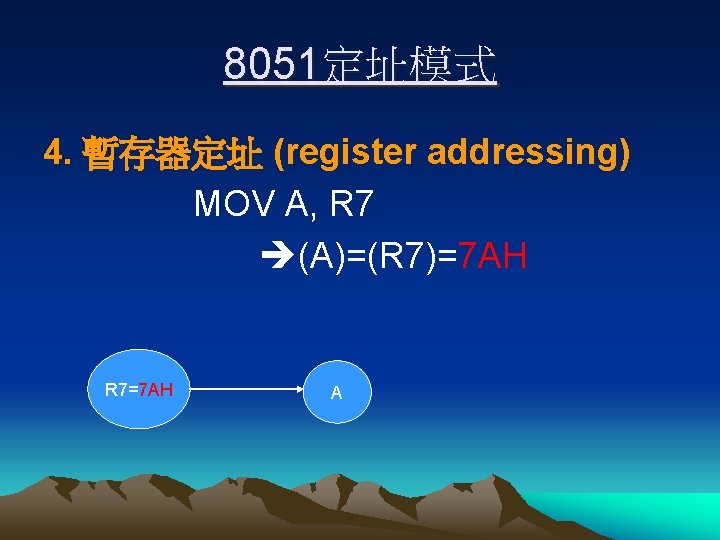
8051定址模式 4. 暫存器定址 (register addressing) MOV A, R 7 (A)=(R 7)=7 AH R 7=7 AH A

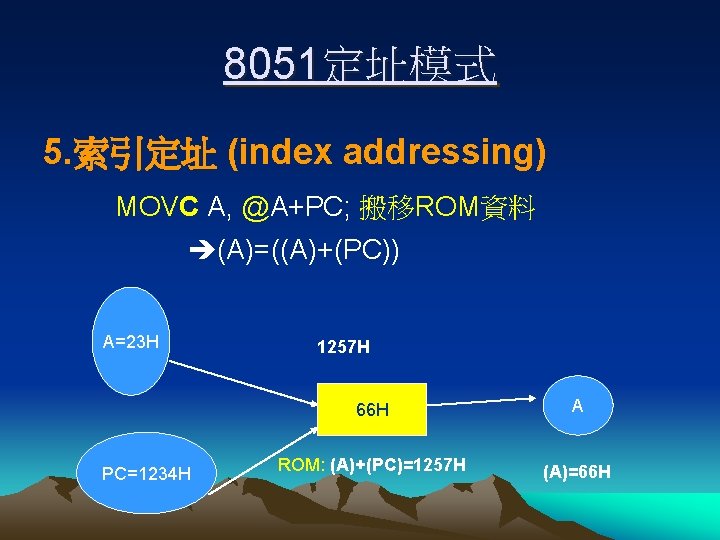
8051定址模式 5. 索引定址 (index addressing) MOVC A, @A+PC; 搬移ROM資料 (A)=((A)+(PC)) A=23 H PC=1234 H 1257 H 66 H A ROM: (A)+(PC)=1257 H (A)=66 H

8051定址模式 5. 索引定址 (index addressing) MOVX A, @A+DPTR; 搬移外部RAM資料 A)+(PC (A)=((A)+(DPTR))=77 H A=23 H 1257 H 66 H DPTR=1234 H A 外部RAM: (A)+(DPTR)=1257 H (A)=66 H

8051指令

符號 • • Rn: R 0~R 7 Ri: R 0, R 1 direct: 0~127 data (常數) 123(十進位) 23 H(十六進位) 10011110 B(二進位)

資料轉移指令-example 1 • MOV A, # 33 H (A)=33 H • MOV A, #01011100 B (A)=5 CH • MOV A, #77 (A)=77 • MOV A, #1 (A)=1 MOV R 1, A ( R 1)=(A)=1

資料轉移指令-3 [1] Given (R 1)=33 H, (33 H)=77 H, (DPTR)=1111 H (1111 H)=66 H MOVX A, @R 1 (A)=(外部RAM(R 1))=((外部RAM (33 H))=77 H MOVX A, @DPTR (A)=((DPTR))=(1111 H)=66 H

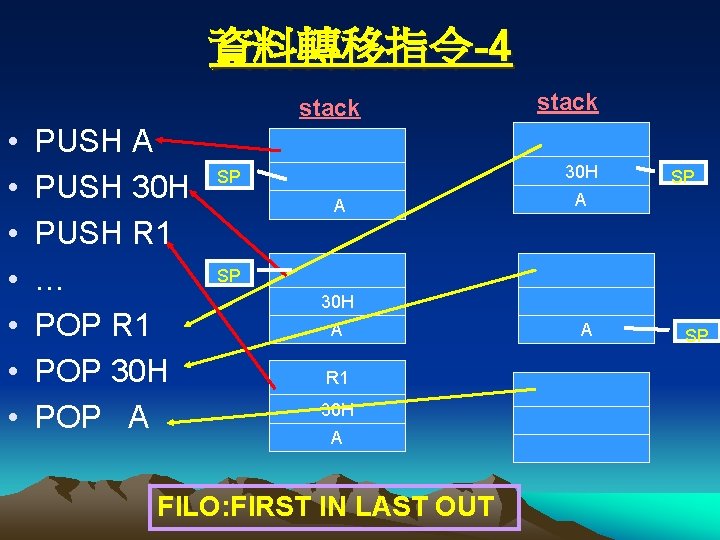
資料轉移指令-4 stack • • PUSH A PUSH 30 H PUSH R 1 … POP R 1 POP 30 H POP A stack 30 H SP A SP 30 H A R 1 30 H A FILO: FIRST IN LAST OUT A SP

資料轉移指令-5 • Given (A)=34 H, (R 1)=56 H, (30 H)=78 H XCH A, 30 H (A)=78 H, (30 H)=34 H XCH A, R 1 (A)=56 H, (R 1)=34 H

算數運算指令 加: ADD, ADDC, INC 減: SUBB, DEC 乘: MUL 除: DIV

算數運算指令-2 • Given (A)=20 H, (R 1)=30 H, (30 H)=66 H, (CY)=1 ADD A, #03 H (A)= (A)+3 H= 20 H+3 H=23 H ADDC A, R 1 (A)= (A)+ (R 1)+ (CY)= 20 H+30 H+1=51 H

l Given (A)=10 INC A ; (A)=(A)+1=11 • Given (A)=20 DEC A ; (A)=(A)-1=19 l Given (R 1)=20 DEC R 1 ; ( R 1)=(R 1)-1=20 -1=19 l Given (A)=30, (R 2)=10, CY=0 SUBB A, R 2 ; (A)=(A)-(R 2)-(CY)=30 -10 -0=20

算數運算指令MUL, DIV • Mul A , B : A, B A＊B • Div A, B : A, B A/B – 商數存於A; 餘數存於B • Given (A)=15, (B)=20 MUL A, B (A)x(B)=15 x 20=300 (A)=1, (B)=44 • Given (A)=17, (B)=4 DIV A, B ; 17/4=4… 1 (A)=4, (B)=1

邏輯運算指令 • ANL, ORL, XOR • RL, RLC, RRC • CLR

• Given (A)=10110010, (R 1)=11110000, (30 H)=22 H [1] ANL A, R 1 ; (A)=(A) and (R 1) (A): 10110010 (R 1): 11110000 ----------10110000 [2] ORL A, #11100000 B ; (A): 10110010 D 0 H: 11100000 -------------11110010=F 0 H

• AND A, 30 H 10110010 ----------0010=22 H • ORL A, @R 1 A or ((R 1))=A or (30 H) =A or 22 H=B 2 H 10110010 --------10110010=B 2 H

l Given (A)=10 H, (R 1)=33 H XRL A, #FFH ; (A)=EFH l XRL A, R 1 ; 00010000 0011 ---------00100011=23 H

RL A ; (A)=(A)*2 l A 7 A 6 A 5 A 4 A 3 A 2 A 1 A 0 0 = A 6 A 5 A 4 A 3 A 2 A 1 A 0 0 l (A)=23 H=00100011 RL A=001000110=46 H

RR A; (A)=(A)/2 l 0 A 7 A 6 A 5 A 4 A 3 A 2 A 1 A 0 =0 A 7 A 6 A 5 A 4 A 3 A 2 A 1 l (A)=23 H=00100011 RR A=00011=0001=11 H

RLC A; (A)=2*(A)+(CY) l CY A 7 A 6 A 5 A 4 A 3 A 2 A 1 A 0 CY = A 6 A 5 A 4 A 3 A 2 A 1 A 0 CY * (CY)=A 7 l Given ( CY)=1, (A)=23 H=00100011 RLC A (CY) 00100011 (CY)=01000111=47 H, (CY)=0

RRC A l (CY) A 7 A 6 A 5 A 4 A 3 A 2 A 1 A 0 (CY) (A) =CY A 7 A 6 A 5 A 4 A 3 A 2 A 1 l (CY) = A 0 l (CY) =1, (A)=23 H=00100011 RRC A (CY) 00100011 (CY) (A)=10010001=91 H (CY) =1

CALL---RET. . . CALL DRLAY MOV A, #56 H. . . DRLAY: MOV R 0, #56 H. . RET.

程式跳躍指令 3 • CJNE A, direct, rel CJNE A, 30 H, LOOP 1 • CJNE A, #data, rel CJNE A, #30 H, LOOP 1 • CJNE Rn, #data, rel CJNE R 2, 30 H, LOOP 1 • CJNE @Ri, #data, rel CJNE @R 1, #30 H, LOOP 1

有條件跳躍4 • JC rel – JC LOOP 1 • JNC rel – JNC LOOP 1 • JB bit, rel – JB PSW. 5, LOOP 1 • JNB bit, rel – JNB 25 H. 5, LOOP 1 • JBC bit, rel – JBC PSW. 5, LOOP 1

布林運算指令 • CLR C CY=0 • CLR bit – CLR P 0. 1=0 – CLR PSW. Z=0 • SETB C • SETB bit CY=1 – SETB P 1. 2=1 – SET TMOD. 3=1

布林運算指令 • ANL C, bit – ANL C, P 3. 1 (CY)=)CY)and P 3. 1 • ANL C, /bit – ANL C, /20 H. 4 • ORL C, bit – ORL C, 23 H. 4 • ORL C, /bit – ORL C, /PSW. 7

布林運算指令 • MOV C, bit – MOV C, PSW. 0 • MOV bit , C – MOV 22 H. 3, C