8 Project Management PERT and CPM techniques for

8. Project Management PERT and CPM: techniques for planning and coordinating large-scale projects. PERT: program evaluation and review technique. CPM : Critical path method ØGraphically displays project activities ØEstimates how long the project will take ØIndicates most critical activities ØShow where delays will not affect project Project Network (precedence) Diagram 2020/11/1 1

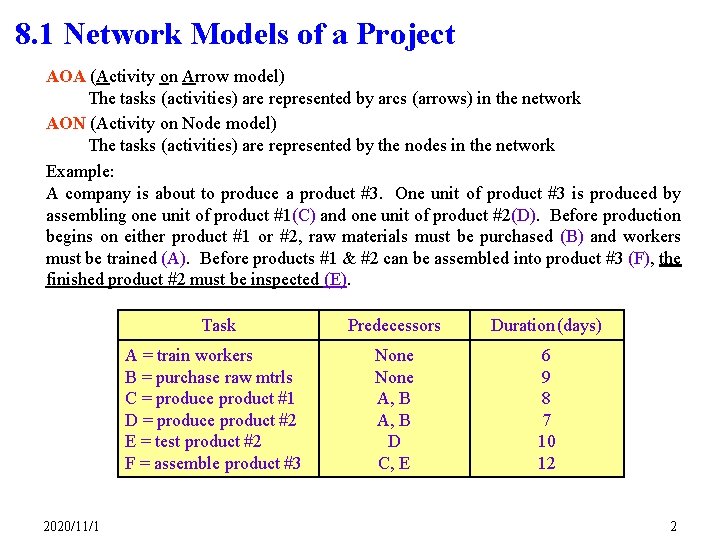
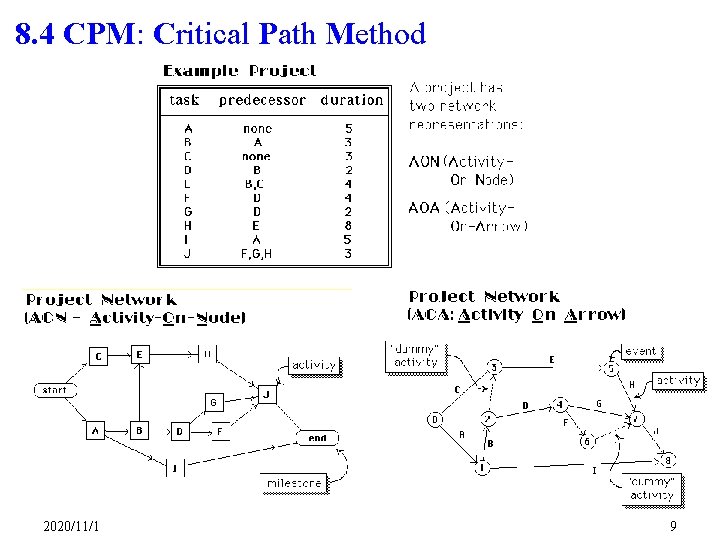
8. 1 Network Models of a Project AOA (Activity on Arrow model) The tasks (activities) are represented by arcs (arrows) in the network AON (Activity on Node model) The tasks (activities) are represented by the nodes in the network Example: A company is about to produce a product #3. One unit of product #3 is produced by assembling one unit of product #1(C) and one unit of product #2(D). Before production begins on either product #1 or #2, raw materials must be purchased (B) and workers must be trained (A). Before products #1 & #2 can be assembled into product #3 (F), the finished product #2 must be inspected (E). 2020/11/1 Task Predecessors Duration (days) A = train workers B = purchase raw mtrls C = produce product #1 D = produce product #2 E = test product #2 F = assemble product #3 None A, B D C, E 6 9 8 7 10 12 2

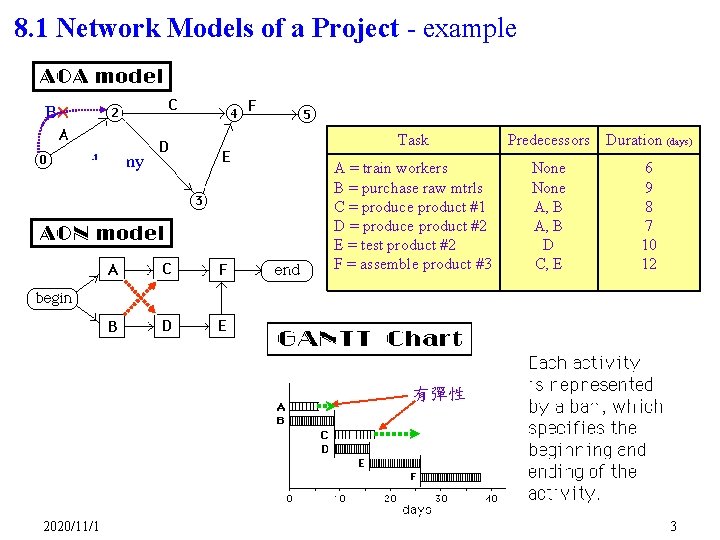
8. 1 Network Models of a Project - example B dummy Task Predecessors Duration (days) A = train workers B = purchase raw mtrls C = produce product #1 D = produce product #2 E = test product #2 F = assemble product #3 None A, B D C, E 6 9 8 7 10 12 有彈性 2020/11/1 3

8. 2 Deterministic time estimates Deterministic: Time estimates that are fairly certain Example of CPM: Computing Algorithm ES: the earliest time that activity can start. EF: the earliest time that activity can finish. LS: the latest time the activity can start and not delay the project. LF: the latest time the activity can finish and not delay the project. These for finding: ü Expected project duration ü Slack time ü The activities on the critical path Steps of problem solving: labeling events computing ES and EF computing LS and LF computing Slack Times 2020/11/1 6 weeks 8 weeks 2 4 11 weeks 1 3 weeks 5 4 weeks Path 1 -2 -4 -5 -6 1 -2 -5 -6 1 -3 -5 -6 3 6 1 week 9 weeks Length (weeks) 18 20 14 Slack 2 0 6 4

8. 3 Probabilistic time estimates Probabilistic : Estimates of times that allow for variation. Probabilistic Estimates - PERT One of the shortcomings of CPM is the assumption that the durations of activities are deterministic, i. e. , known with certainty. PERT assume that the duration of each activity is random variable with known mean and standard variation, and derives a probability distribution for the project completion time. Assumptions of PERT The duration of an activity is a random variable with BETA distribution. The durations of the activities are statistically independent. The critical path (computed assuming expected values of the durations) always requires a longer total time than any other path. The Central Limit Theorem can be applied so that the sum of the durations of the activities on the critical path has approximately a NORMAL distribution. 2020/11/1 5

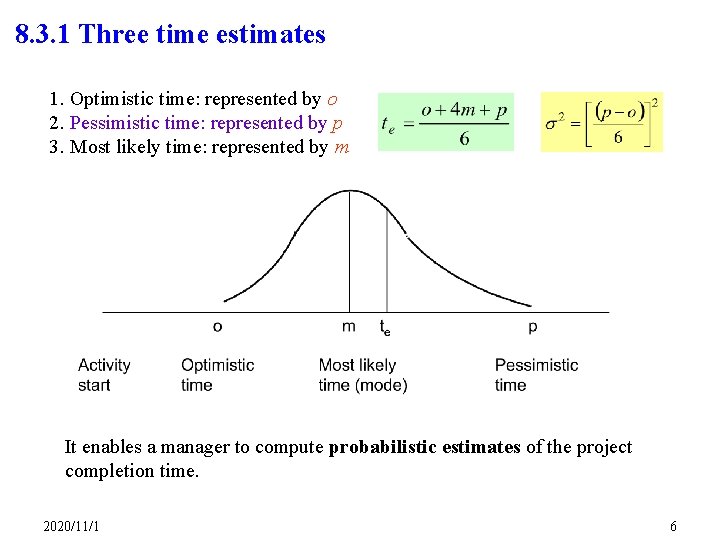
8. 3. 1 Three time estimates 1. Optimistic time: represented by o 2. Pessimistic time: represented by p 3. Most likely time: represented by m It enables a manager to compute probabilistic estimates of the project completion time. 2020/11/1 6

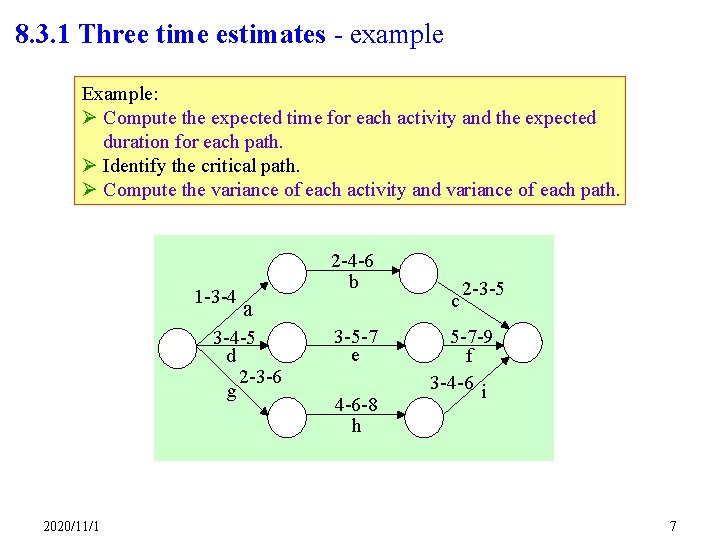
8. 3. 1 Three time estimates - example Example: Ø Compute the expected time for each activity and the expected duration for each path. Ø Identify the critical path. Ø Compute the variance of each activity and variance of each path. 1 -3 -4 2 -4 -6 b a 3 -4 -5 d 2 -3 -6 g 2020/11/1 3 -5 -7 e 4 -6 -8 h c 2 -3 -5 5 -7 -9 f 3 -4 -6 i 7

8. 3. 1 Three time estimates - example Path Activity o m p te Path total (TE) a-b-c a b c 1 3 4 2 4 6 2 3 5 2. 83 4. 00 3. 17 10. 00 0. 97 d-e-f d e f 3 4 5 3 5 7 9 4. 00 5. 00 7. 00 16. 00 1. 00 N(16, 1) g-h-i g h i 2 3 6 4 6 8 3 4 6 3. 33 6. 00 4. 17 13. 50 1. 07 N(TE, ) The expected completion time of the project is 16 days. What is the probability that it is completed within 17 days? ì T - 16 17 - 16 ü { } £ = £ P T 17 P í ý = P{X î 2020/11/1 1 1 þ £ 1} 8

8. 4 CPM: Critical Path Method 2020/11/1 9

8. 4. 1 Project Network (AOA) A connected, directed network without circuits, with a unique source and unique sink. The vertices are called "events“. The arcs are called "activities", each with an associated nonnegative duration. Predecessors & Successors The project network indicates the order in which activities may be performed. Activity B cannot begin until activity A has been completed. üActivity A is a predecessor of activity B üActivity B is a successor of activity A 2020/11/1 10

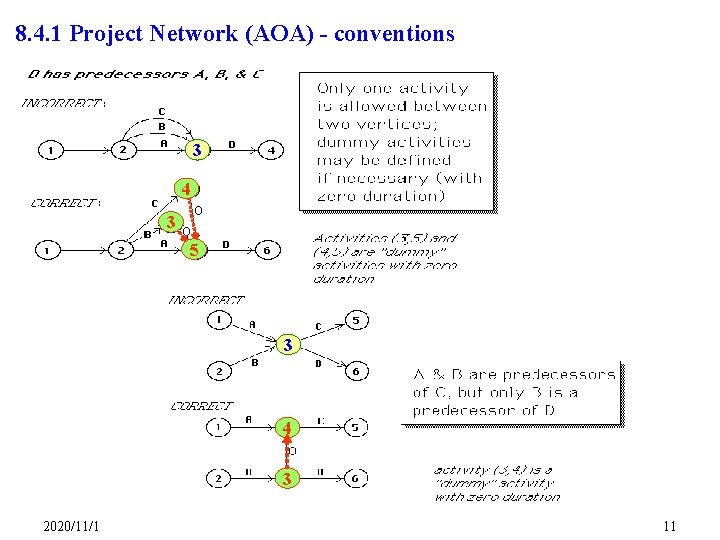
8. 4. 1 Project Network (AOA) - conventions 3 4 3 5 3 4 3 2020/11/1 11

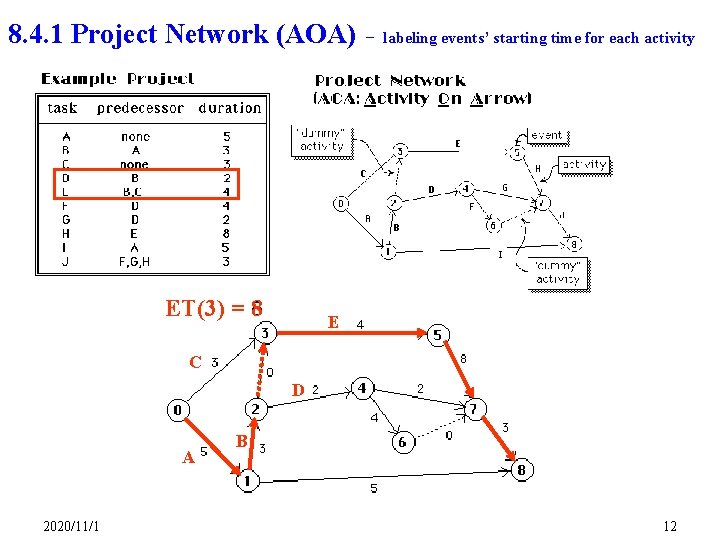
8. 4. 1 Project Network (AOA) – labeling events’ starting time for each activity ET(3) = 8 E C D A 2020/11/1 B 12

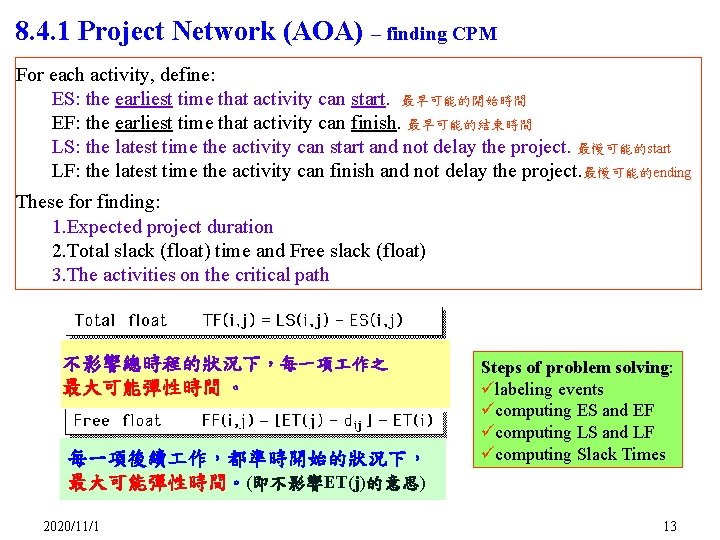
8. 4. 1 Project Network (AOA) – finding CPM For each activity, define: ES: the earliest time that activity can start. 最早可能的開始時間 EF: the earliest time that activity can finish. 最早可能的結束時間 LS: the latest time the activity can start and not delay the project. 最慢可能的start LF: the latest time the activity can finish and not delay the project. 最慢可能的ending These for finding: 1. Expected project duration 2. Total slack (float) time and Free slack (float) 3. The activities on the critical path 不影響總時程的狀況下，每一項 作之 最大可能彈性時間 。 每一項後續 作，都準時開始的狀況下， 最大可能彈性時間。(即不影響ET(j)的意思) 2020/11/1 Steps of problem solving: ülabeling events ücomputing ES and EF ücomputing LS and LF ücomputing Slack Times 13

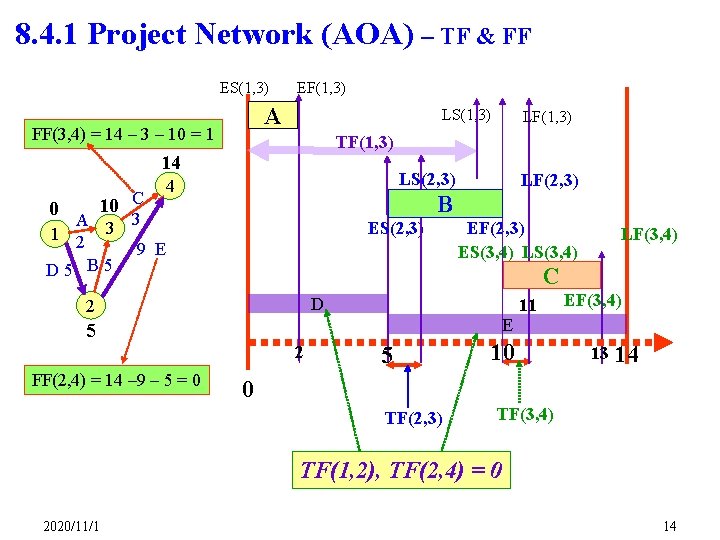
8. 4. 1 Project Network (AOA) – TF & FF ES(1, 3) EF(1, 3) A FF(3, 4) = 14 – 3 – 10 = 1 LS(1, 3) TF(1, 3) 14 10 C 0 LS(2, 3) 4 LF(2, 3) B A 3 3 1 2 9 E D 5 B 5 ES(2, 3) EF(2, 3) ES(3, 4) LF(3, 4) C D 2 E 5 2 FF(2, 4) = 14 – 9 – 5 = 0 LF(1, 3) 5 11 10 EF(3, 4) 13 14 0 TF(2, 3) TF(3, 4) TF(1, 2), TF(2, 4) = 0 2020/11/1 14

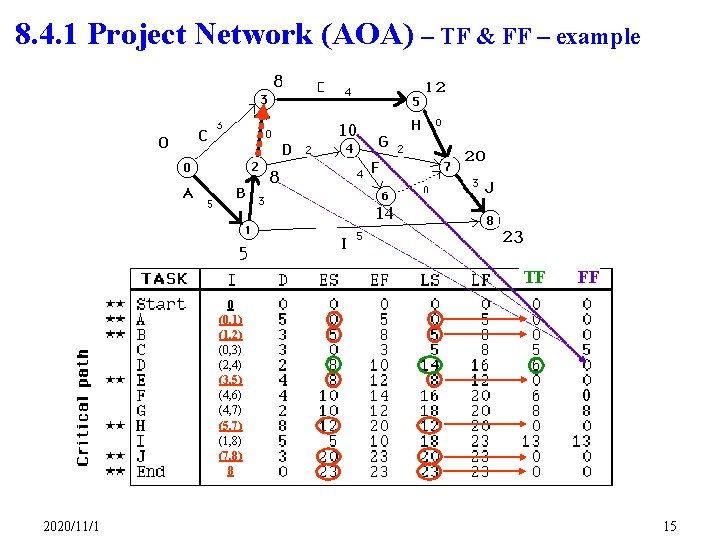
8. 4. 1 Project Network (AOA) – TF & FF – example 10 14 TF 0 (0, 1) (1, 2) (0, 3) (2, 4) (3, 5) (4, 6) (4, 7) (5, 7) (1, 8) (7, 8) 8 2020/11/1 FF 0 15

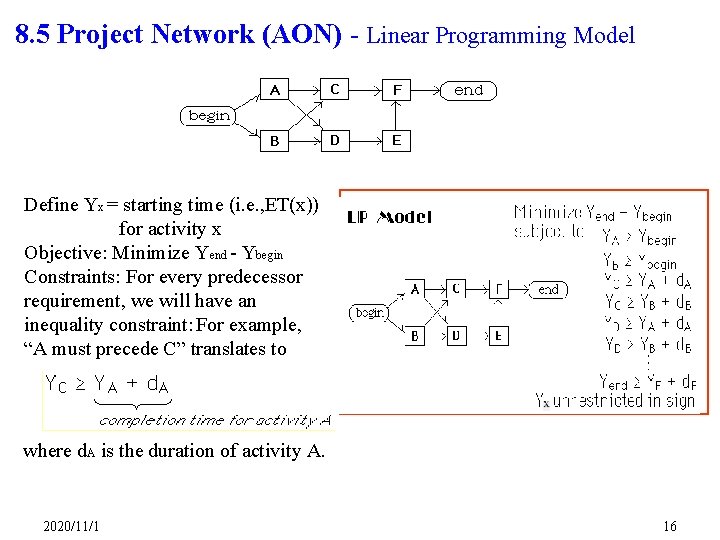
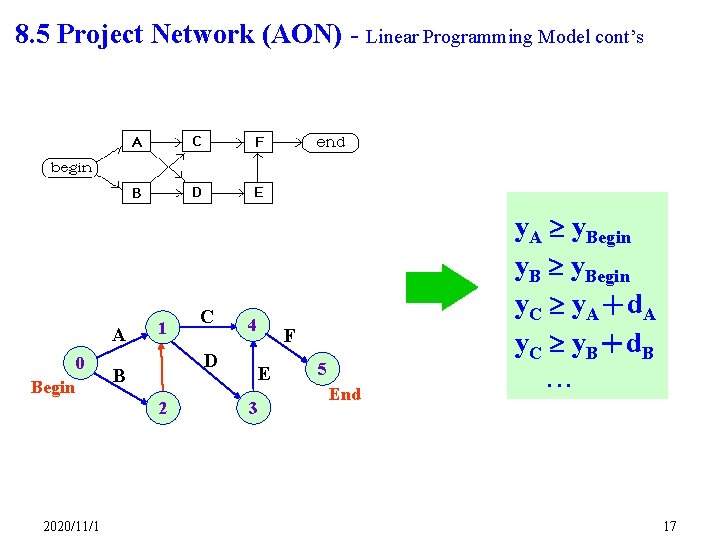
8. 5 Project Network (AON) - Linear Programming Model Define Yx = starting time (i. e. , ET(x)) for activity x Objective: Minimize Yend - Ybegin Constraints: For every predecessor requirement, we will have an inequality constraint: For example, “A must precede C” translates to where d. A is the duration of activity A. 2020/11/1 16

8. 5 Project Network (AON) - Linear Programming Model cont’s A 0 Begin 1 D B 2 2020/11/1 C 4 y. A y. Begin y. C y. A＋d. A y. C y. B＋d. B F E 3 5 End . . . 17

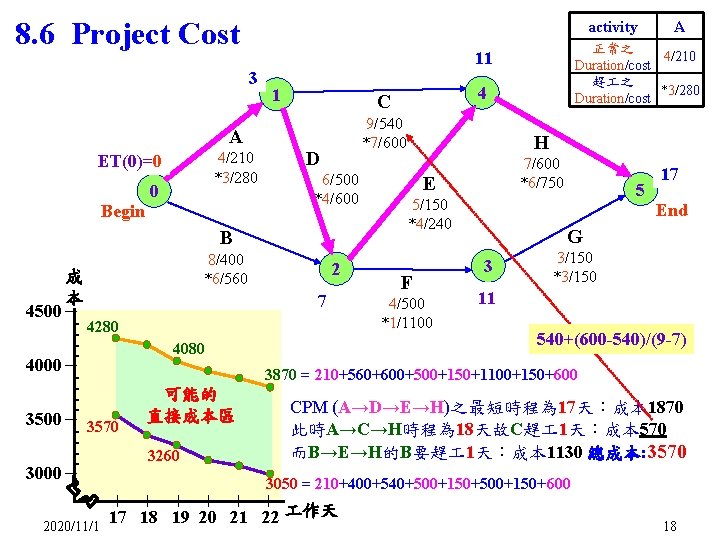
8. 6 Project Cost activity 43 A Begin 0 6/500 *4/600 B 2020/11/1 2 10 7 4080 9/540 *7/600 H 7/600 *6/750 E 5/150 *4/240 F 4/500 *1/1100 5 22 17 End G 3 14 11 ? 3/150 *3/150 540+(600 -540)/(9 -7) 3870 = 210+560+600+500+150+1100+150+600 可能的 直接成本區 CPM (A→D→E→H)之最短時程為 17天：成本 1870 此時A→C→H時程為 18天故C趕 1天：成本 570 而B→E→H的B要趕 1天：成本 1130 總成本: 3570 3050 = 210+400+540+500+150+600 － － 3260 － － 成 本 4500－ - 4280 4000－ 3570 3000－ 8/400 *6/560 4 C D 4/210 *3/280 ET(0)=0 正常之 4/210 Duration/cost 趕 之 *3/280 Duration/cost 11 15 1 A 17 18 19 20 21 22 作天 18

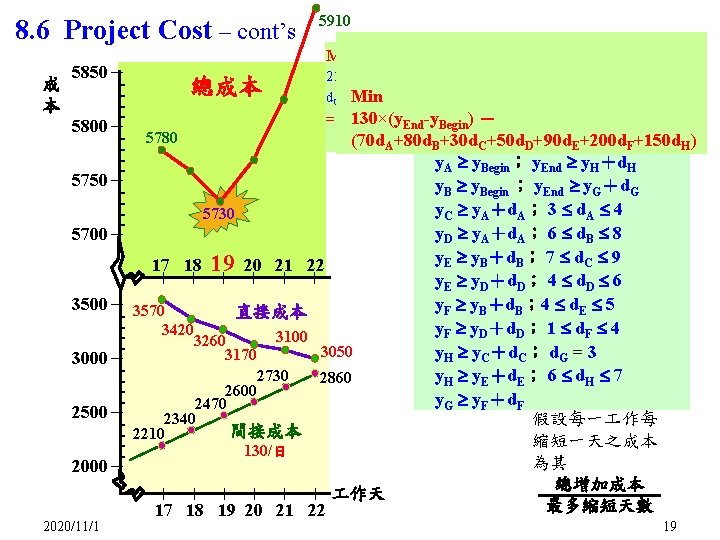
8. 6 Project Cost – cont’s 210+400+540+500+150+600+70(4 -d. A)+80(8 -d. B) +30(9 d. C)+50(6 -d Min D)+90(5 -d. E)+200(4 -d. F)+150(7 -d. H)+130×(y. End-y. Begin) 總成本 = 6840－ (70 d +80 d 130×(y － C+50 d. D+90 d. E+200 d. F+150 d. H) End. A-y Begin. B)+30 d Minimize ? ? ? (70 d. AEnd +80 d +130×(y -y. Begin ) C+50 d B+30 d D+90 d. E+200 d. F+150 d. H) 5780 5730 － 20 21 22 － 19 － － － 17 18 － 5850－ 5800－ 5750－ 5700－ Min 2020/11/1 － － － 3500－ 3570 直接成本 3420 3100 3260 3050 3170 3000－ 2730 2860 2600 2470 2500－ 2340 間接成本 - 2210 130/日 2000－ 作天 17 18 19 20 21 22 － 成 本 5910 y. A y. Begin； y. End y. H＋d. H y. Begin ； y. End y. G＋d. G y. C y. A＋d. A； 3 d. A 4 y. D y. A＋d. A； 6 d. B 8 y. E y. B＋d. B； 7 d. C 9 y. E y. D＋d. D； 4 d. D 6 y. F y. B＋d. B； 4 d. E 5 y. F y. D＋d. D； 1 d. F 4 y. H y. C＋d. C； d. G = 3 y. H y. E＋d. E； 6 d. H 7 y. G y. F＋d. F 假設每一 作每 縮短一天之成本 為其 總增加成本 最多縮短天數 19