8 Geometric Operations Geometric operations change image geometry







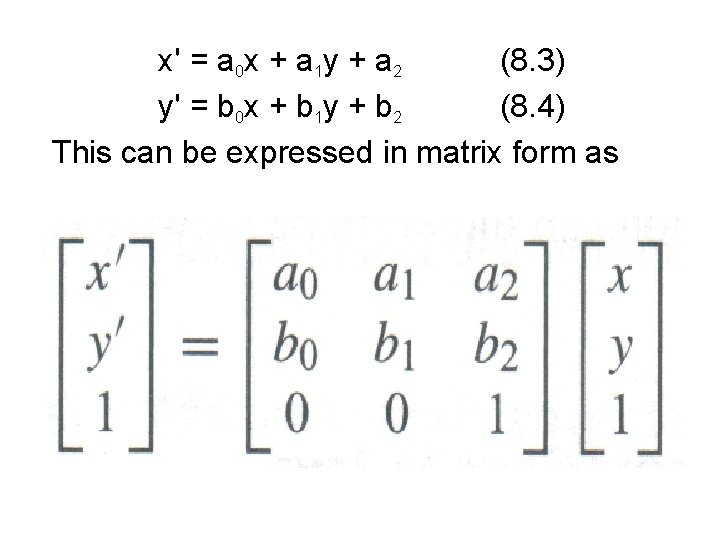





- Slides: 13

8. Geometric Operations • Geometric operations change image geometry by moving pixels around in a carefully constrained way. • We might do this to remove distortions inherent in the imaging process, or to introduce a deliberate distortion that matches one image with another. • In this chapter, we will consider simple operations such as scaling and rotation.

Simple techniques • There are some simple techniques for manipulating image geometry. • An image can be enlarged by an integer factor, n, simply by copying each pixel to an n x n block of pixels in the output image. • This technique is fast, and has been a standard feature of specialised image processing hardware.

• An obvious disadvantage is that it cannot be used to expand an image by some arbitrary, non‑integer factor. • Another problem is that greatly enlarged images have a very 'blocky' appearance. • This may not bother us in applications where we merely wish to examine pixels more closely, but is of serious concern otherwise.

• There are similar problems with the technique of shrinking an image by subsampling its array of pixels. • First, the technique cannot be used to reduce image dimensions by an arbitrary factor. • Second, subsampling can eliminate information from the image completely. • One solution to this latter problem is to turn an n x n block of pixels in the input image into a single pixel in the output image. • The value of each output pixel must be representative of the corresponding block in the input image. • The median and mean grey level of the block can be used.

Fig. 8. 1 Shrinking. (a) Original image. (b) Subsampling (c) Mean of n x n block. (d) Median of n x n block.

• Figure 8. 1 compares subsampling with the n x n mean and n x n median approaches for a real image of a face. • In this case, there is little to choose between the mean and median images. • The subsampled image is clearly inferior, with data loss leading to an apparent change in facial expression.

Affine transformation • An arbitrary geometric transformation will move a pixel at coordinates (x, y) to a new position, (x’, y'), given by a pair of transformation equations, X’ = Tx (X, Y), (8. 1) Y’ = TY (X, Y) (8. 2) • Tx and Ty are typically expressed as polynomials in x and y. • In their simplest form, they are linear in x and y, giving us an affine transformation,
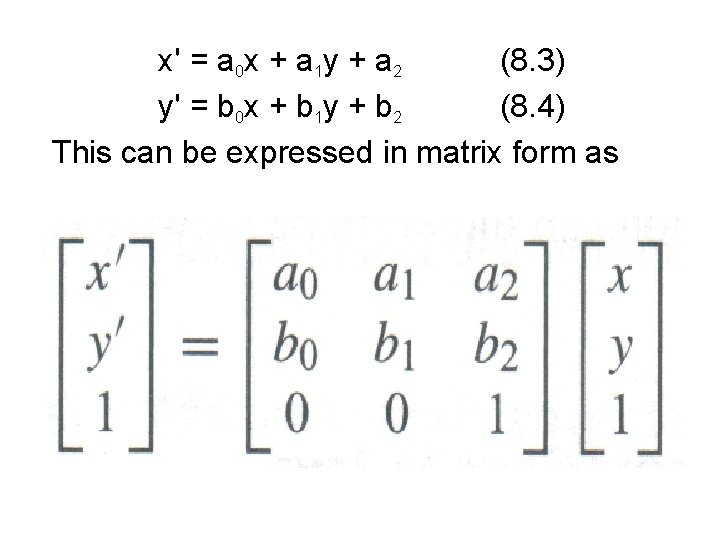
x' = a 0 x + a 1 y + a 2 (8. 3) y' = b 0 x + b 1 y + b 2 (8. 4) This can be expressed in matrix form as

• Under an affine transformation, straight lines are preserved and parallel lines remain parallel. • Translation, scaling, rotation and shearing are all special cases of Equations 8. 3 and 8. 4.

• For example, a translation of 3 pixels down and 5 pixels to the right is x' = x + 5, y' = y + 3. The corresponding aftine transformation matrix is

• Table 8. 1 specifies how the elements of the transformation matrix are computed for selected special cases of affine transformation. Table 8. 1 Transformation coefficients for some simple affine transformations.

Rotation • Suppose, for example, that we wish to rotate an image by an angle θ about the origin. • This is accomplished with the transformation matrix

Algorithm 8. 1 Image rotation by forward mapping