8 Evaluation Methods Errors and Error Rates Precision

8. Evaluation Methods Errors and Error Rates Precision and Recall Similarity Cross Validation Various Presentations of Evaluation Results Statistical Tests 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 1

How to evaluate/estimate error • Resubstitution – one data set used for both training and for testing • Holdout (training and testing) – 2/3 for training, 1/3 for testing • Leave-one-out – If a data set is small • Cross validation – 10 -fold, why 10? – m 10 -fold CV 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 2

Error and Error Rate • Mean and Median – mean = 1/n xi – weighted mean = ( wixi)/ wi – median = x(n+1)/2 if n is odd, else (xn/2+x(n/2)+1)/2 • Error – disagreement btwn y and y’ (predicted) – 1 if they disagree, 0 otherwise (0 -1 loss l 01) – Other definitions depending on the output of a predictor such as quadratic loss l 2, absolute loss l‖ 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 3

• Error estimation – Error rate e = #Errors/N, where N is the total number of instances – Accuracy A = 1 - e 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 4

Precision and Recall O|Pred P’ve N’ve P’ve TP FN N’ve FP TN • False negative and false positive • Types of errors for k classes = k 2 -k – k = 3, 3*3 -3 = 6, k = 2, 2*2 -2 = 2 • Precision (wrt the retrieved) – P = TP/(TP+FP) • Recall (wrt the total relevant) – R = TP/(TP+FN) R • Precision×Recall (PR) and PR gain – PR gain = (PR’ – PR 0)/PR 0 • Accuracy – A = (TP+TN)/(TP+TN+FP+FN) 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) P 5

Similarity or Dissimilarity Measures • Distance (dissimilarity) measures (Triangle Inequality) – Euclidean – City-block, or Manhattan – Cosine (pi, pj)= [ (pikpjk)/ (pik)2 (pjk)2] • Inter-clusters and intra-clusters – Single linkage vs. complete linkage • Dmin = min|pi - pj|, two data points • Dmax= max|pi - pj| – Centroid methods • Davg= 1/(ninj) |pi – pj| • Dmean= |mi - mj|, two means 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 6

k-Fold Cross Validation • Cross validation – 1 fold for training, the rest for testing – rotate until every fold is used for training – calculate average Fold 1 Fold 2 Fold 3 • m k-fold cross validation – reshuffle data, repeat XV for m times – what is a suitable k? • Model complexity – use of XV • tree complexity, training/testing error rates 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 7

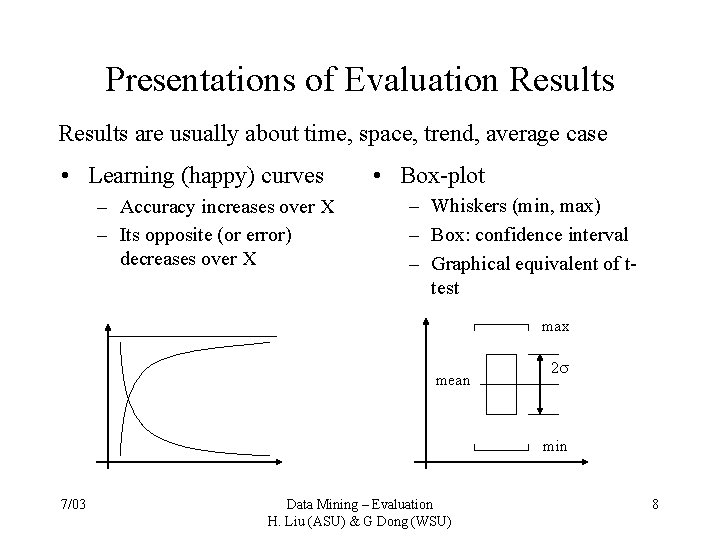
Presentations of Evaluation Results are usually about time, space, trend, average case • Learning (happy) curves – Accuracy increases over X – Its opposite (or error) decreases over X • Box-plot – Whiskers (min, max) – Box: confidence interval – Graphical equivalent of ttest max mean 2 min 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 8

Statistical Tests • • • Null hypothesis and alternative hypothesis Type I and Type II errors Student’s t test comparing two means Paired t test comparing two means Chi-Square test – Contingency table 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 9

Null Hypothesis • Null hypothesis (H 0) – No difference between the test statistic and the actual value of the population parameter – E. g. , H 0: = 0 • Alternative hypothesis (H 1) – It specifies the parameter value(s) to be accepted if the H 0 is rejected. – E. g. , H 1: != 0 – two-tailed test – Or H 1: > 0 – one-tailed test 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 10

Type I, II errors • Type I errors ( ) – Rejecting a null hypothesis when it is true (FN) • Type II errors ( ) – Accepting a null hypothesis when it is false (FP) – Power = 1 – • Costs of different errors – A life-saving medicine appears to be effective, which is cheap and has no side effect (H 0: non-effective) • Type I error: it is effective, not costly • Type II error: it is non-effective, very costly 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 11

Test using Student’s t Distribution • Use t distribution for testing the difference between two population means is appropriate if – – The population standard deviations are not known The samples are small (n < 30) The populations are assumed to be approx. normal The two unknown 1 = 2 • H 0: ( 1 - 2) = 0, H 1: ( 1 - 2) != 0 – Check the difference of estimated means normalized by common population means • degree of freedom and p level of significance – df = n 1 + n 2 – 2 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 12

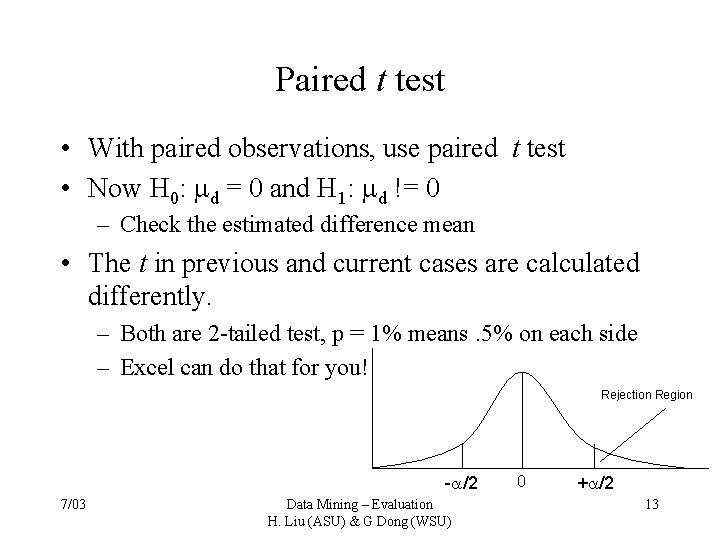
Paired t test • With paired observations, use paired t test • Now H 0: d = 0 and H 1: d != 0 – Check the estimated difference mean • The t in previous and current cases are calculated differently. – Both are 2 -tailed test, p = 1% means. 5% on each side – Excel can do that for you! Rejection Region - /2 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 0 + /2 13

Chi-Square Test (the goodness-of-fit) • Testing a null hypothesis that the population distribution for a random variable follows a specified form. • The chi-square statistic is calculated: C 1 C 2 2 k 2 = (Aij – i=1 j=1 Eij)2 / Eij • degree of freedom df = k-m-1 – k = num of data categories – m = num of parameters estimated I-1 A 12 R 1 I-2 A 21 A 22 R 2 C 1 C 2 N Rejection Region • 0 – uniform, 1 - Poisson, 2 - normal – Each cell should be at least 5 • One-tail test 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 14

Bibliography • W. Klosgen & J. M. Zytkow, edited, 2002, Handbook of Data Mining and Knowledge Discovery. Oxford University Press. • L. J. Kazmier & N. F. Pohl, 1987. Basic Statistics for Business and Economics. • R. E. Walpole & R. H. Myers, 1993. Probability and Statistics for Engineers and Scientists (5 th edition). MACMILLAN Publishing Company. 7/03 Data Mining – Evaluation H. Liu (ASU) & G Dong (WSU) 15