8 Differentiating some Trig Functions most slides Christine

8: Differentiating some Trig Functions most slides © Christine Crisp

Differentiating some Trig Functions A reminder of the rules for differentiation developed so far! Ø Ø ( I call these functions the simple ones. ) Ø The chain rule ( for functions of a function ): where

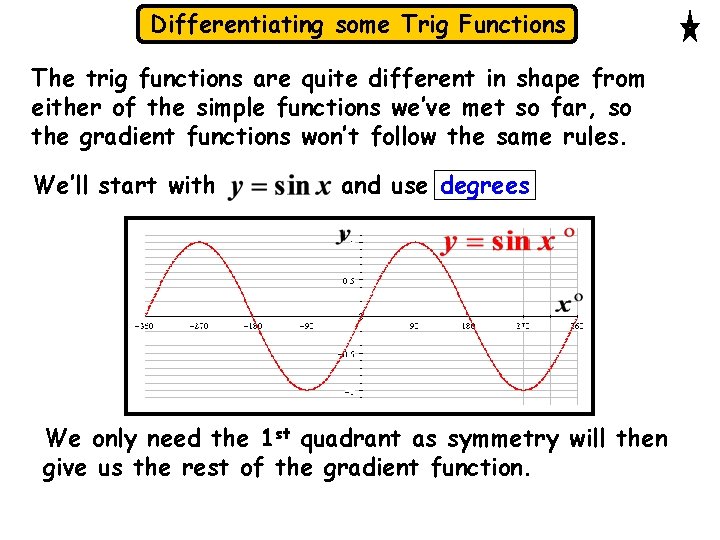
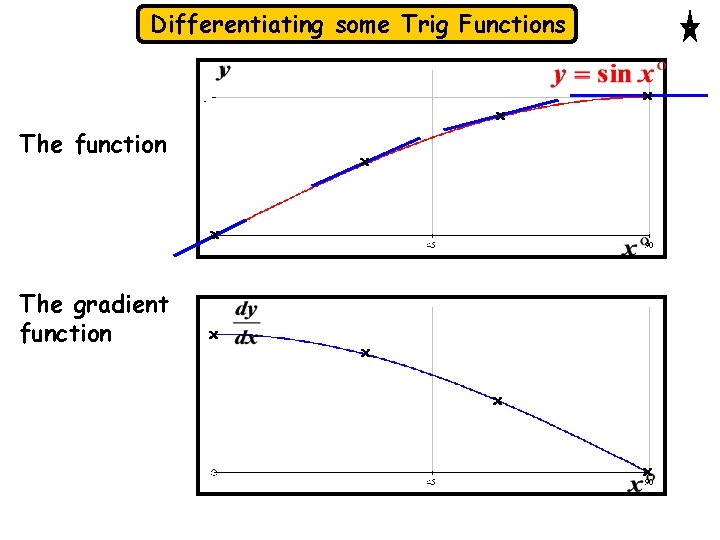
Differentiating some Trig Functions The trig functions are quite different in shape from either of the simple functions we’ve met so far, so the gradient functions won’t follow the same rules. We’ll start with and use degrees We only need the 1 st quadrant as symmetry will then give us the rest of the gradient function.

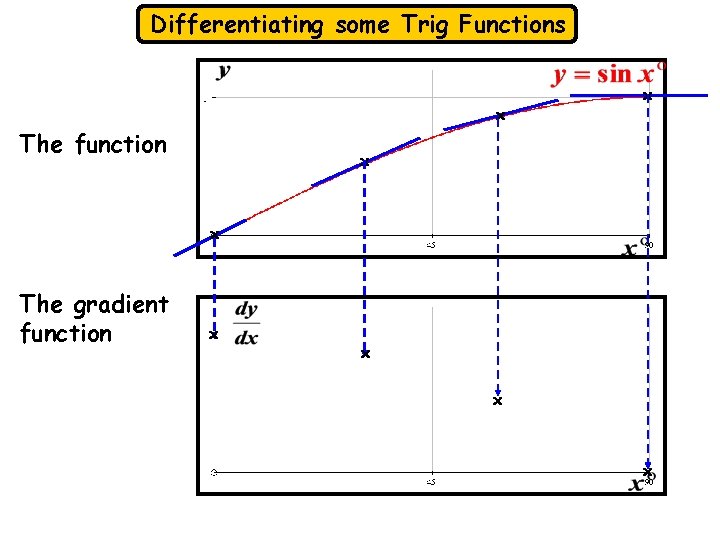
Differentiating some Trig Functions x The function x x x The gradient function x x

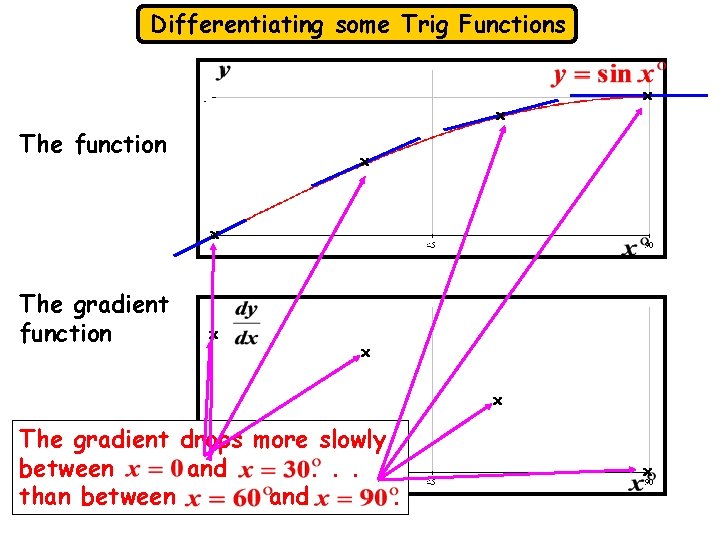
Differentiating some Trig Functions x The function x x x The gradient drops more slowly between and. . . than between and. x

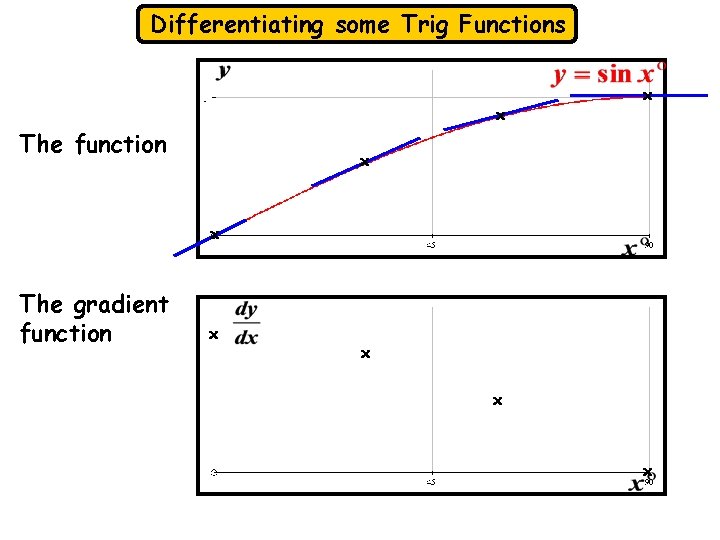
Differentiating some Trig Functions x The function x x x The gradient function x x

Differentiating some Trig Functions x The function x x x The gradient function x x

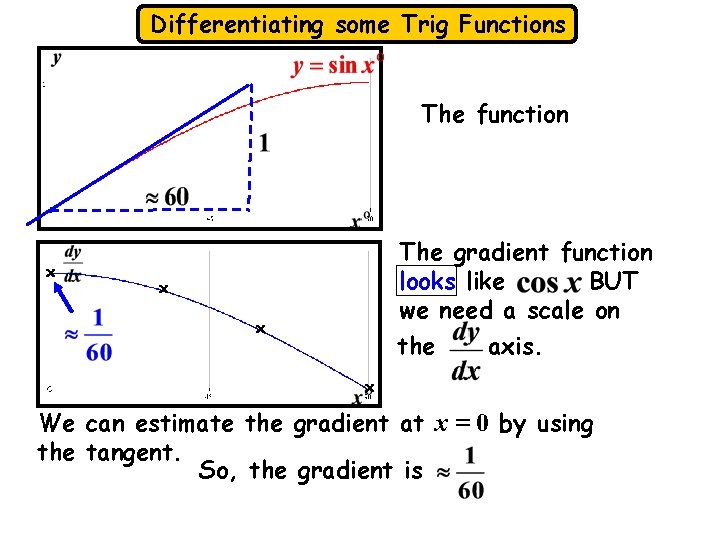
Differentiating some Trig Functions The function x The gradient function looks like BUT we need a scale on x x the axis. x We can estimate the gradient at x = 0 by using the tangent. So, the gradient is

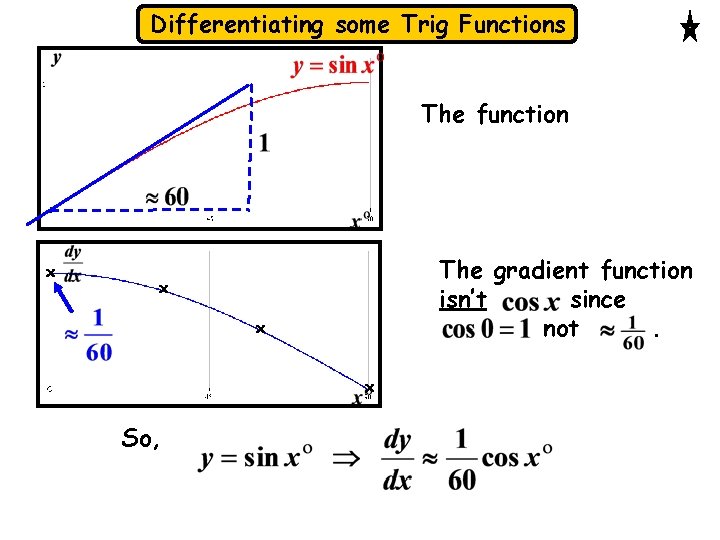
Differentiating some Trig Functions The function x The gradient function isn’t since not. x x x So,

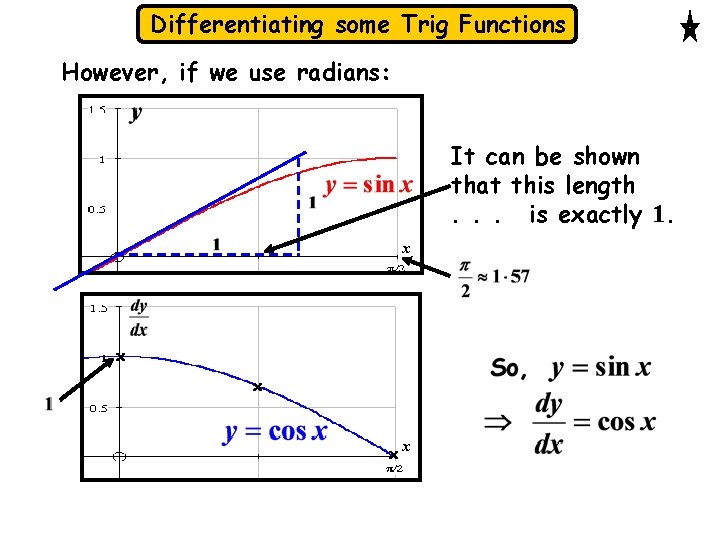
Differentiating some Trig Functions However, if we use radians: It can be shown that this length. . . is exactly 1. x xx

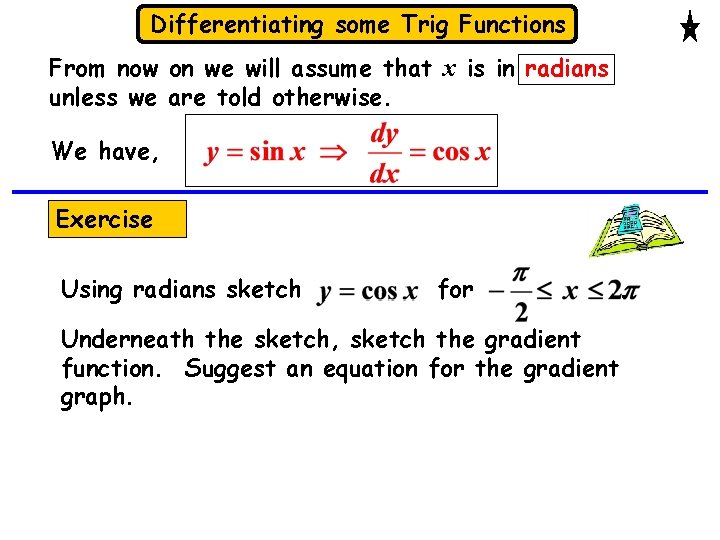
Differentiating some Trig Functions From now on we will assume that x is in radians unless we are told otherwise. We have, Exercise Using radians sketch for . Underneath the sketch, sketch the gradient function. Suggest an equation for the gradient graph.

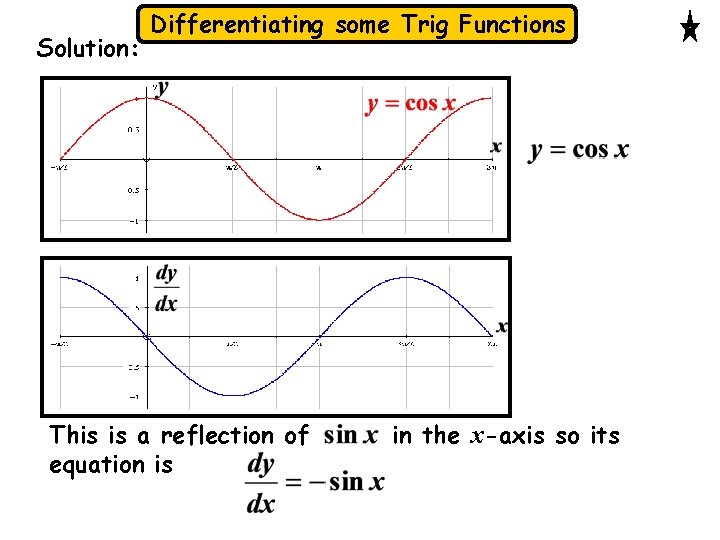
Solution: Differentiating some Trig Functions This is a reflection of equation is in the x-axis so its

Differentiating some Trig Functions SUMMARY Ø If x is in radians, N. B. We have not proved these results; just shown they look correct. We need a bit more theory before we can differentiate the trig function. This is done in a later presentation.

Differentiating some Trig Functions Compound Trig Functions We can use the chain rule to differentiate trig functions of a function. e. g. 1 Find the gradient of at the point where. N. B. We(a) don’t needfind to the put brackets round 3 x. Solution: First gradient function: Let N. B. Radians!

Differentiating some Trig Functions e. g. 2 Differentiate What would you let u equal in this example? Solution: If we write as we can easily see that the inner function is. So, let

Differentiating some Trig Functions e. g. 3 Differentiate Be careful! This isn’t the same as Solution: Let

Differentiating some Trig Functions Exercise Differentiate the following with respect to x: 1. 2. 3. 4. Solutions: Let 1.

Differentiating some Trig Functions 2. 3. Let

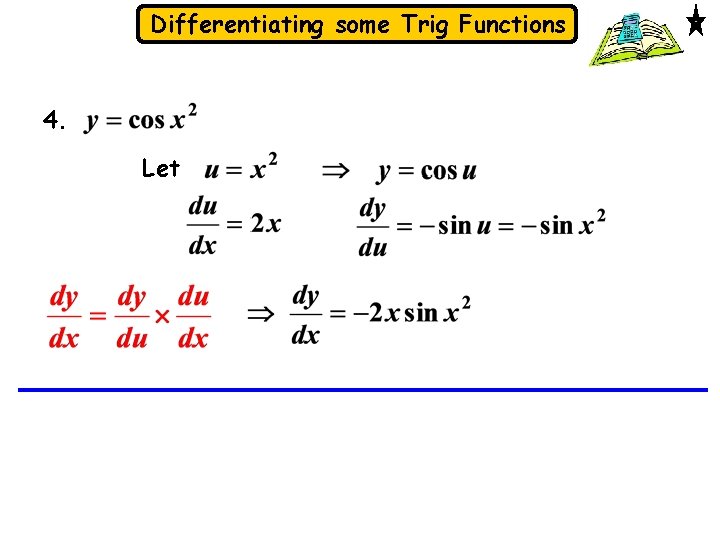
Differentiating some Trig Functions 4. Let

Differentiating some Trig Functions We can now differentiate the trig function by writing y = tan x

Differentiating some Trig Functions So, This answer can be simplified: Also, So, is defined as

Differentiating some Trig Functions Summary

Differentiating some Trig Functions Inverse trig functions

Differentiating some Trig Functions y = sin (4 x + 2) let y = sin u and u = 4 x + 2 Answer

Differentiating some Trig Functions y = sin x tan 2 x use the product rule Answer

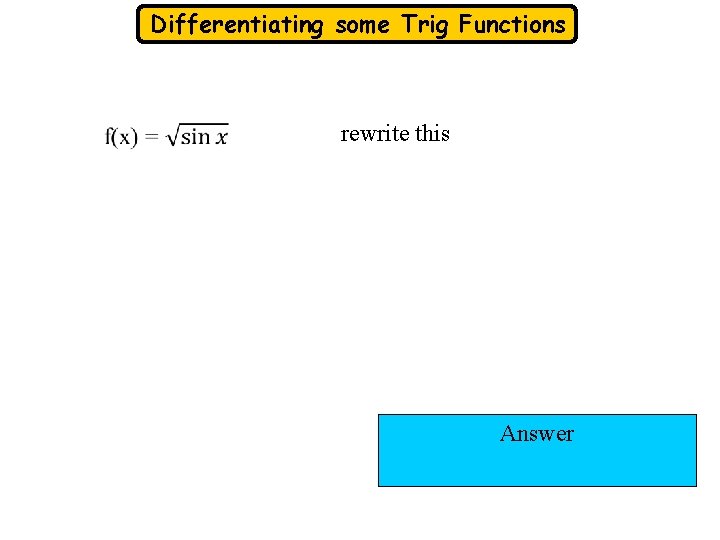
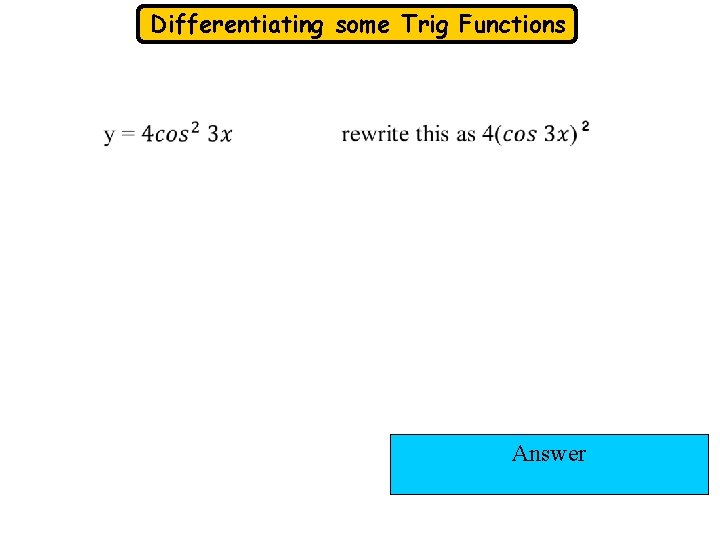
Differentiating some Trig Functions rewrite this Answer

Differentiating some Trig Functions Answer

Differentiating some Trig Functions f’(x) = 10 Answer sec² 5 x tan 5 x

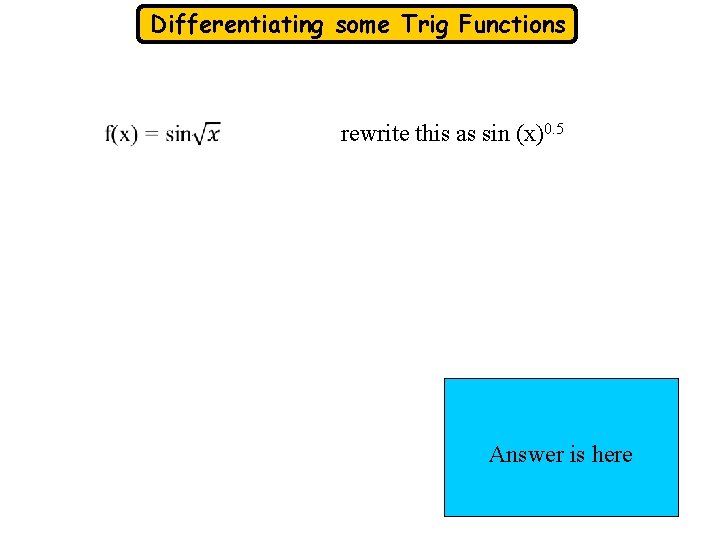
Differentiating some Trig Functions rewrite this as sin (x)0. 5 Answer is here

Differentiating some Trig Functions