8 7 Modeling Motion Using Parametric Equations Objectives

8. 7 Modeling Motion Using Parametric Equations Objectives: Model the motion of a projectile using parametric equations. Solve problems related to the motion of a projectile, its trajectory, and range.

Joke of the day! What do you call a lazy baby kangaroo? A pouch potato!

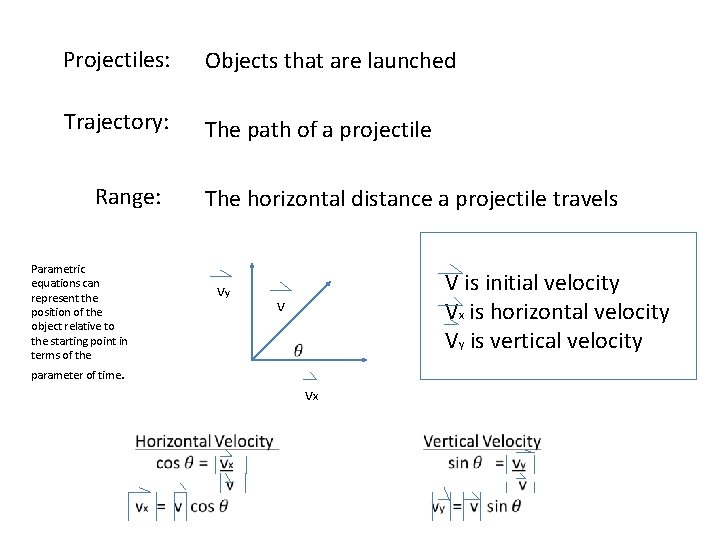
Projectiles: Objects that are launched Trajectory: The path of a projectile Range: Parametric equations can represent the position of the object relative to the starting point in terms of the parameter of time. The horizontal distance a projectile travels vy V is initial velocity Vx is horizontal velocity Vy is vertical velocity v vx

Find the horizontal velocity and vertical velocity of a stone kicked with an initial velocity of 18 feet per second at an angle of 37° with the ground. Ex. 1) Horizontal distance: •

Vertical Displacement: •

Ex. 2) Sammy Baugh of the Washington Redskins has the record for the highest average punting record for a lifetime average of 45. 16 yards. Suppose that he kicked the ball with an initial velocity of 26 yards per second at an angle of 72°. a. ) How far has the ball traveled horizontally and what is its vertical height at the end of 3 seconds? b. ) Suppose that the kick returner lets the ball hit the ground instead of catching it. What is the hang time?

Ex. 3) One of the earliest pitchers in the history of pro baseball to throw a perfect game was Addie Joss of the Cleveland Naps in 1908. Suppose that he throws a ball at an angle of 5. 1° with the horizontal at a speed of 85 mph. The distance of the pitcher’s mound to home plate is 60. 5 feet. If Mr. Joss releases the ball 2. 9 feet above the ground, how far above the ground is the ball when it crosses home plate?