8 6 Knapsack Ciphers The Concept l l

8. 6. Knapsack Ciphers

The Concept l l l At the core of the Knapsack cipher is the Knapsack problem: Given positive integers a 1, a 2, …, an & S, which of the ai integers add up to S. As an equation, solve for xi either 1 or 0: S = a 1 x 1 + a 2 x 2 + … + a n xn Example: a 1 = 2, a 2=3, a 3=4, a 4=7, a 5=11, a 6=13, a 7=16 and S=18 Solutions: 16+2, 13+3+2, 11+4+3, 11+7, thus (1, 0, 0, 0, 1); (1, 1, 0, 0, 0, 1, 0); (0, 1, 1, 0, 0); (0, 0, 0, 1, 1, 0, 0)

S = a 1 x 1 + a 2 x 2 + … + a n xn complexity Good vs. Bad l Difficult Calculations when n is large: Trial and Error l 2 n possibilities for (x 1, x 2, …, xn) infeasible to find all the solutions when n=100 or more Easier to find solution for certain a 1, a 2, …, an: aj=2 J-1 S = a 1 x 1 + a 2 x 2 + … + an xn = 20 x 1 + 21 x 2 + … + 2 n-1 xn = xn … x 2 x 1 on binary form (base 2) Thus for the solution is: write S in the binary form!

Super Increasing Sequences l l A type of sequence a 1, a 2, …, an for which it is easier but not trivial to solve knapsack problems super increasing sequence if jth term > sum of the preceding values (j-1) Σk ak < aj for j = 2, 3, …, n l Example 1: (2, 3, 7, 13, 28) is super increasing (2, 3, 4, 7, 11, 13, 16) is not l Example 2 (pb 3): aj+1 > 2 aj super increasing sequence Example 3 (pb 2): aj < 2 j-1 NOT super increasing sequence l

Example of solving Knapsack problem for super increasing sequence l (a 1=2, a 2=3, a 3=7, a 4=13, a 5=28) and S=40 l l S≥ a 5 x 5 = 1 since a 1+a 2+a 3+a 4< a 5=28 S- x 5 a 5 = 12 < a 4 =13 x 4 =0 S- (x 5 a 5 + x 4 a 4 )=12 ≥ a 3 x 3 = 1 S- (x 5 a 5 + x 4 a 4+ x 3 a 3 )=5 ≥ a 2 x 2 = 1 S- (x 5 a 5 + x 4 a 4+x 3 a 3 + x 3 a 3 )=2 ≥ a 1 x 1 = 1 l Solution: (1, 1, 1, 0, 1) l l l

Super Increasing Algorithm l S = a 1 x 1 + a 2 x 2 + … + a n xn

Public cryptosystem: Knapsack Ciphers based on super increasing sequences Merkle and Hellman [Me. He 78]. l Based on a transformed not super increasing sequence b 1, b 2, …, bn from a simple super increasing a 1, a 2, …, an l Given m> 2 an and (ω, m)=1 find ώ ώ ω ≡ 1(mod m) ώ ≡ ωΦ(m)-1 (mod m) Then Find bj bj ≡ ω aj (mod m) aj ≡ ώ bj (mod m)

Observations l IF S= b 1 x 1 + b 2 x 2 + … + bn xn Then ώ S ≡ ώ b 1 x 1 + …+ ώ bn xn ≡ a 1 x 1 + …+ an xn (mod m) l b 1, b 2, …, bn is not super increasing not easy to solve S= b 1 x 1 + b 2 x 2 + … + bn xn l a 1, a 2, …, an is super increasing easy to solve S 0= a 1 x 1 + a 2 x 2 + … + a n x n where ώ S ≡ S 0(mod m) l One needs to know m, ω & ώ

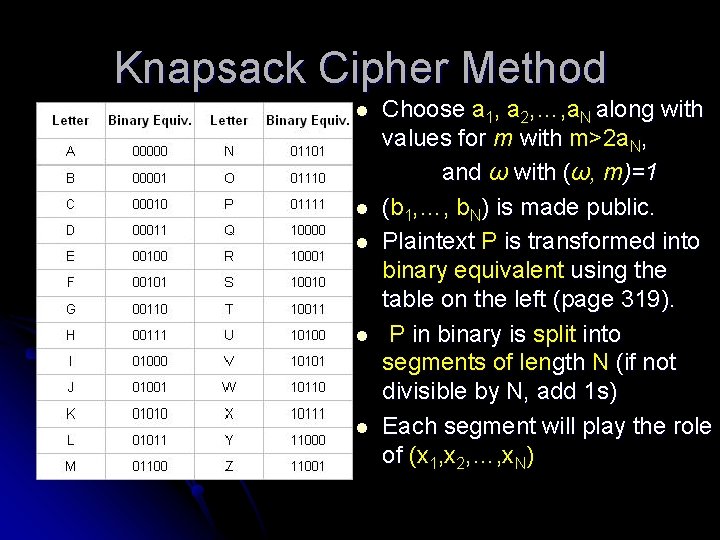
Knapsack Cipher Method l l l Choose a 1, a 2, …, a. N along with values for m with m>2 a. N, and ω with (ω, m)=1 (b 1, …, b. N) is made public. Plaintext P is transformed into binary equivalent using the table on the left (page 319). P in binary is split into segments of length N (if not divisible by N, add 1 s) Each segment will play the role of (x 1, x 2, …, x. N)

Knapsack Cipher Method (cont. ) l For each segment (x 1, x 2, …, x. N) in P, compute S= b 1 x 1 + b 2 x 2 + … + b. N x. N l C= Ciphertext = the set of S generated from each (x 1, x 2, …, x. N) in P = difficult to find (x 1, x 2, …, x. N) from S l Decryption when m & ω (thus ώ) are known: easy to solve for (x 1, x 2, …, x. N) with S 0= a 1 x 1 + a 2 x 2 + … + a n x n where ώ S ≡ S 0(mod m)

Example P=BUY NOW=000011010011000011010110 l A=(3, 5, 9, 20, 44); m=89; ω=67 l P= ([0, 0, 1], [1, 0, 0], [1, 1, 0, 0, 0], [0, 1, 1, 0, 1], [0, 1, 1, 1, 0], [1, 0, 1, 1, 0]) = matrix notation Encryption (BT = transpose of B = Vertical vector B) l B≡ ω A (mod 89) = (23, 68, 69, 5, 11) l C= PBT = (11, 92, 91, 148, 142, 97 ) Decryption: l ώ ≡ ωΦ(m)-1 (mod m) =6787= 4 (mod 89) l S 0 ≡ ώ S (mod m) ≡ 4*C = (44, 368, 364, 592, 568, 388) ≡ [44, 12, 8, 58, 34, 32] (mod 89) l Use Knapsack algorithm to solve S 0= a 1 x 1 + a 2 x 2 + … + an xn l For example: 44= 44(1) 00001 B 12=9 (1) + 3(1) 10100 U 8= 3(1)+ 5 (1) 11000 Y l

l l Cryptanalysis Knapsack Ciphers were a popular form of public key cryptography. In 1982, Shamir (see [Sh 84] & [Od 90]) efficient method to solve S= b 1 x 1 + b 2 x 2 + … + b. N x. N, thus find x 1 x 2…x. N from the transformed public key b 1 b 2 …b. N There exists an algorithmto find the solution using O(P(n)) bit operations where P is a polynomial instead of the exponential time Adjustments can be made to protect it from such weaknesses, such as using several successive transformations with (ωi, mi) to form b 1 b 2 …b. N